Thi học kì 2 môn Toán 8: Cho hình lập phương có cạnh là 5 cm. Diện tích xung quanh của hình lập phương là

Phần I: Trắc nghiệm khách quan (3đ)

Bài 1: (2đ) Khoanh tròn vào chữ cái đứng trước câu trả lời đúng:

1) Giá trị của phân thức \(\dfrac{{4x{{(x – 2)}^2}}}{{{x^2} – 4}}\) tại x = -1 bằng:

A.  12

B. -12

C.  \(\dfrac{1}{{12}}\)

D. \( – \dfrac{1}{{12}}\)

2) Điều kiện để giá trị phân thức \(\dfrac{{x + 1}}{{{x^3} – 2{x^2} + x}}\) được xác định là:

A.  \(x \ne 0\)

B.  \(x \ne 1\)

C. \(x \ne 0\) và \(x \ne 1\)

D. \(x \ne 0\) và \(x \ne  – 1\)

3) Phương trình \(\dfrac{{{x^2} – 1}}{{x + 1}} = 1\) có nghiệm là:

A. -1

B. 2

C. 2 và -1

D. -2

4) Điều kiện xác định của phương trình:\(1 + \dfrac{x}{{3 – x}} = \dfrac{{5x}}{{(x + 2)(3 – x)}} + \dfrac{2}{{x + 2}}\) là:

A. \(x \ne 3\)

B. \(x \ne  – 2\)

C. \(x \ne 3\) và \(x \ne  – 2\)

D. \(x \ne 3\) hoặc \(x \ne  – 2\)

5) Nếu \(a \ge b\) thì \(10 – 2a\)…..\(10 – 2b\). Dấu thích hợp trong ô trống là:

A. <                            B. >

C. \( \le \)                            D. \( \ge \)

6) x= 1 là nghiệm của bất phương trình:

A. \(3x + 3 > 9\)

B. \( – 5x > 4x + 1\)

C. \(x – 2x <  – 2x + 4\)

D. \(x – 6 > 5 – x\)

7) Cho hình lập phương có cạnh là 5 cm. Diện tích xung quanh của hình lập phương là:

A.  \(25c{m^2}\)                   B. \(125c{m^2}\)

C. \(150c{m^2}\)                   D. \(100c{m^2}\)

8) Cho hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao lần lượt là: 5cm ; 3cm ; 2cm. Thể tích của hình hộp chữ nhật là:

A. \(54c{m^3}\)                    B. \(54c{m^2}\)

C. \(30c{m^2}\)                    D. \(30c{m^3}\)

Bài 2: (2đ) Điền dấu “x” vào ô thích hợp:

Phần II: Tự luận (7đ)

Bài 1: (2đ) Giải bất phương trình sau:

\(\dfrac{{1 – 2x}}{4} – 2 < \dfrac{{1 – 5x}}{8}\)

Bài 2: (2đ) Giải bài toán bằng cách lập phương trình:

Một đội máy kéo dự định mỗi ngày cày được 40 ha. Khi thực hiện, mỗi ngày cày được 52 ha. Vì vậy, đội không những đã cày xong trước thời hạn 2 ngày mà còn cày thêm được 4 ha nữa. Tính diện tích ruộng mà đội phải cày theo kế hoạch đã định?

Bài 3: (3đ) Cho \(\Delta \)ABC vuông tại A, đường cao AH (H\( \in \) BC). Biết BH = 4cm ; CH = 9cm. Gọi I, K lần lượt là hình chiếu của H lên AB và AC. Chứng minh rằng:

a) Tứ giác AIHK là hình chữ nhật.

b) Tam giác AKI  đồng dạng với tam giác ABC.

c) Tính diện tích \(\Delta \)ABC.

Phần I: Trắc nghiệm khách quan (3đ)

Bài 1: ( 2đ): Mỗi câu đúng cho 0,25 điểm:

Bài 2: (1đ) Mỗi ý đúng cho 0,25 điểm.

a). Đ                      b). S

c). Đ                      d). S

Phần II: Tự luận (7đ)

Bài 3: (1đ)

\(\dfrac{{1 – 2x}}{4} – 2 < \dfrac{{1 – 5x}}{8}\)

\( \Leftrightarrow \dfrac{{2(1 – 2x)}}{8} – \dfrac{{16}}{8} < \dfrac{{1 – 5x}}{8}\)

\(\begin{array}{l} \Leftrightarrow \dfrac{{2 – 4x – 16 – 1 + 5x}}{8} < 0\\ \Leftrightarrow \dfrac{{x – 15}}{8} < 0\\ \Leftrightarrow x – 15 < 0\\ \Leftrightarrow x < 15\end{array}\)

Vậy nghiệm của bất phương trình là:\(\left\{ {x|x < 15} \right\}\)

Bài 4: (2đ)

+ Gọi x là diện tích ruộng đội cày theo kế hoạch (ha; x > 40)
+ Diện tích ruộng đội đã cày được là: x + 4  (ha)

+ Số ngày đội dự định cày là: \(\dfrac{x}{{40}}\) (ha) . Số ngày đội đã cày là: \(\dfrac{{x + 4}}{{52}}\) (ha)

+ Đội cày xong trước thời hạn 2 ngày nên ta có ptrình: \(\dfrac{x}{{40}}\) – \(\dfrac{{x + 4}}{{52}}\) = 2

+ Giảỉ phương trình được:  \(x = 360\)

+ Kết luận : diện tích ruộng đội cày theo kế hoạch là 360 ha.

Bài 5: (3đ)

Vẽ hình đúng

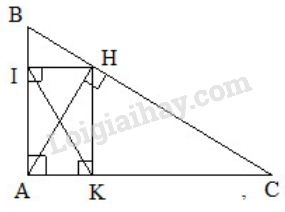
a) Tứ giác AIHK có

 \(\widehat {IAK} = \widehat {AKH} = \widehat {AIH} = 90^\circ \,\,(gt)\)

Suy ra tứ giác AIHK là hcn (Tứ giác có 3 góc vuông)

b)  \(\widehat {ACB} + \widehat {ABC} = 90^\circ \)

   \(\widehat {HAB} + \widehat {ABH} = 90^\circ \)

Suy ra : \(\widehat {ACB} = \widehat {HAB}\left( 1 \right)\)

Tứ giác AIHK là hcn \( \Rightarrow \)    \(\widehat {HAB} = \widehat {AIK}\,\,\,\,\,\,\left( 2 \right)\)

Từ (1) và (2) \( \Rightarrow \widehat {ACB} = \widehat {AIK}\)

\( \Rightarrow \) \(\Delta \)AIK đồng dạng với \(\Delta \)ABC (g – g)

c) \(\Delta \)HAB đồng dạng với \(\Delta \)HCA (g- g)

\( \Rightarrow \dfrac{{HA}}{{HC}} = \dfrac{{HB}}{{HA}}\)

\( \Rightarrow H{A^2} = HB.HC = 4.9 = 36\) \( \Rightarrow HA = 6(cm)\).

  \({S_{ABC}} = \dfrac{1}{2}AH.BC = 39(c{m^2}\)