
Bài 1.
a) Viết tập hợp các số nguyên a sao cho -5 ≤ a < 5
b) Tìm ƯCLN (360, 480)
Bài 2. Tính
a) A = (7 – 9)3 + (-5)7 : (-5)5 + 20100
b) B = [2.(-2)2 + 1) : (-3)2] + 9.7 – (-2)6
Bài 3. Tìm x ∈ Z, biết:
a) 15 ⋮ x b) 2x ⋮ 4 = 8
c) |x| < 4
Bài 4. Tìm số tự nhiên m nhỏ nhất sao cho khi chia m cho 3; 5 và 7 có dư lần lượt là 1; 3; 5
Bài 5. Hình vẽ bên có bao nhiêu đoạn thẳng

a) Kể tên các tia đối nhau gốc N
b) Kể tên các tia trùng nhau gốc N
Bài 6. Trên tia Ox lấy các điểm A, B, C sao cho OA = 1cm; OB = 4 cm; OC = 7cm
a) Tính AB, AC và BC
Advertisements (Quảng cáo)
b) So sánh AB + BC và AC. Điểm B có là trung điểm của AC không? Tại sao?

Bài 1.
a) Ta có: M = {-5, -4, -3, -2, -1, 0, 1, 2, 3, 4}
b) Ta có: 360 = 23.32.4; 480 = 25.3.5
⇒ ƯCLN (360, 480) = 25.3.5
Bài 2. a) A = (-2)3 + (-5)2 + 1 = -8 + 25 + 1 = 18
b) B = 9 : 9 + 63 – 64 = 0
Bài 3. a) Vì x ∈ Z và 15 ⋮ x ⇒ x ∈ {±1; ±3; ±5; ± 15}
b) 2x : 4 = 8 ⇒ 2x= 32 ⇒ 2x = 25 ⇒ x = 5
Advertisements (Quảng cáo)
c) Vì x ∈ Z ⇒ |x| ∈ N; |x| < 4 ⇒ |x| = 0; |x| = 1; |x| = 2; |x| = 3
⇒ x ∈ {0, ±1; ± 2; ±3}
Bài 4. Vì m chia cho 3 dư là 1 ⇒ (m + 2) ⋮ 3
Tương tự: (m + 2) ⋮ 5 và (m + 2) ⋮ 7
Lại có BCNN (3, 5, 7) = 105 ⇒ (m + 2) ⋮ 105
Số tự nhiên nhỏ nhất chia hết cho 105 (khác 0) là 105
⇒ m + 2 = 105 ⇒ m = 103
Bài 5. Hình vẽ bên có 6 đọan thẳng
a) Các tia đối nhau gốc N là : NM và NP, NM và NQ
b) Các tia trùng nhau góc M là: MN, MP, My.
Bài 6.
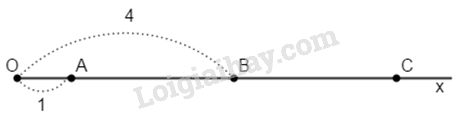
a) A, B thuộc tia Ox mà OA < OB (1 < 4) nên điểm A nằm giữa hai điểm O và B
Ta có: OA + AB = OB
1 + AB = 4
AB = 4 – 1 = 3 (cm).
Chứng minh tương tự ta có OA < OC (1 < 7) nên A nằm giữa hai điểm O và C, ta có:
OA + AC = OC
1 + AC = 7
AC = 7 – 1 = 6 (cm).
Chứng minh tương tự ta có BC = 3 (cm),
b) Ta có AB + BC = 3 + 3 = 6 (cm) ⇒ AB + BC = AC (= 6cm).
Vì A, B, C thuộc tia Ox mà OA < OB< OC (1 < 4 < 7) nên B nằm giữa hai điểm A và C và AB = BC = 3cm. Do đó B là trung điểm của đoạn AC.







