
Bài 1. Tính : A = 200 – 188 : [26 – (32.10 – 78).5]
Bài 2. Tìm x ∈ Z, biết:
a) (3x + 22) : 8 + 10 = 12
b) -12 < 3x ≤ 18
Bài 3. Tìm các số x, y nguyên sao cho (x – 2)(y + 1) = -2
Bài 4. Tìm ƯCLN (192; 102); BCNN (216; 270).
Bài 5. Tìm số tự nhiên m nhỏ nhất, khác 0, biết rẳng m ⋮ 3; m ⋮ 5; m ⋮ 7
Bài 6. Cho 10 điểm trong đó có ba điểm thẳng hàng. Hỏi có bao nhiêu đường thẳng phân biệt được tạo thành đi qua hai điểm trong số các điểm ở trên?
Bài 7. Trên tia Ax lấy hai điểm H và K sao cho AH = 5cm; AK = 10 cm.
a) Trong ba điểm A, H, K điểm nào nằm giữa hai điểm còn lại? Vì sao?
b) Tính độ dài đoạn thẳng HK.
c) Gọi M là trung điểm của đoạn thẳng HK. Tính độ dài AM.

Bài 1.
A = 200 – 188 : [26 – (32.10 – 78).5] = 200 – 188 : [64 – 12.5]
Advertisements (Quảng cáo)
= 200 – 188 : 4 = 200 – 47 = 153
Bài 2.
a) (3x + 22) : 8 + 10 = 12 ⇒ (3x + 22) : 8 = 12 – 10
⇒ 3x + 22 = 8.2 ⇒ 3x = 16 – 22 ⇒ x = (-6) : 3 = -2
b) -12 < 3x ≤ 18 ⇒ 3x = -9; 3x = -6; 3x = -3; 3x = 0; 3x = 3; 3x = 6; 3x = 9; 3x = 12; 3x = 15; 3x = 18
⇒ x ∈ {-3, -2, -1, 0, 1, 2, 3, 4, 5, 6}
Bài 3. Vì -2 = (-2).1 = 2.(-1) nên ta có:
x – 2 = -2 và y + 1 = 1 ⇒ x = 0 và y = 0
x – 2 = 1 và y + 1 = -2 ⇒ x = 3 và y = -3
Advertisements (Quảng cáo)
x – 2 = 2 và y + 1 = -1 ⇒ x = 4 và y = -2
x – 2 = -1 và y + 1 = 2 ⇒ x = 1 và y = 1
Bài 4.
+ Ta có: 192 = 26.3; 102 = 2.3.17 ⇒ ƯCLN(192, 102) = 6
+ Ta có: 216 = 23.33; 270 = 2.33.5 ⇒ BCNN(216, 270) = 23.33.5 = 1080
Bài 5. BCNN(3, 5, 7) = 105
Vậy m = 105
Bài 6. Giả sử trong 10 điểm đã cho không có ba điểm nào thẳng hàng thì số đường thẳng phân biệt được tạo thành là:
9 + 8 + 8 + 6 + 5 + 4 + 3+ 2 + 1 = 45 (đường thẳng).
Nhưng vì trong 10 điểm trên có ba điểm thẳng hàng nên số đường thẳng vẽ được là:
45 – 2 = 43 (đường thẳng).
Bài 7.
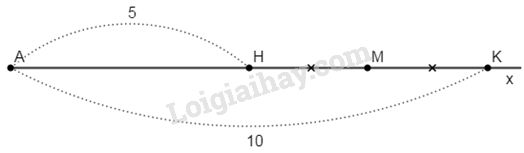
a) Vì H, K thuộc tia Ax mà AH < AK (5 < 10) nên điểm H nằm giữa hai điểm A và K
b) H nằm giữa hai điểm A và K (cmt) nên:
AH + HK = AK
5 + HK = 10
HK = 10 – 5 = 5 (cm)
c) M là trung điểm của đoạn thẳng HK, ta có:
\(MH = MK =\dfrac {{HK} }{ 2} = \dfrac{5 }{ 2} = 2,5(cm)\)
Vì H nằm giữa hai điểm A và K nên HA và HK là hai tia đối nhau. M là trung điểm của HK nên HM và HA là hai tia đối nhau nên H nằm giữa hai điểm A và M ta có:
AM = HA + HM = 5 + 2,5 = 7,5 (cm).







