
A. PHẦN CHUNG (80%, gồm 40 câu)
1. : Tìm tập xác định của hàm số \(y = \sqrt {3 – \sin 2x} \)
A. \(R{\rm{\backslash }}\left\{ {\left. x \right|\,\sin 2x < 0} \right\}\).
B. R
C. \(R{\rm{\backslash }}\left\{ {\left. {k2\pi } \right|\,k \in Z} \right\}\).
D. Một tập hợp khác.
2. : Đường cong trong hình vẽ bên là một phần của đồ thị hàm số nào trong bốn hàm số được liệt kê trong các phương án A, B, C, D dưới dây?
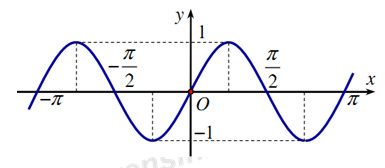
A. \(y = \cos 2x\).
B. \(y = \sin \,x\).
C. \(y = \sin 2x\).
D. \(y = \cos x\).
3. : Tìm chu kì của hàm số \(y = \sin \,x – \cos 4x\).
A. \(4\pi \).
B. \(3\pi \).
C. \(2\pi \).
D. Không có chù kỳ.
4. : Một lớp có 21 học sinh nam và 14 học sinh nữ. Hỏi có bao nhiêu cách chọn một học sinh tham gia sinh hoạt câu lạc bộ nghiên cứu khoa học?
A. 21. B. 35.
C. 14. D. 294.
5. : Có bao nhiêu số tự nhiên có 4 chữ số khác nhau đôi một?
A. 5040. B. 9000.
C. 1000. D. 4536.
6. : Có 5 bì thư khác nhau và 5 con tem khác nhau. Hỏi có bao nhiêu cách dán tem vào bì thư sao cho mỗi bì thư chỉ dán một con tem?
A. 25. B. 120.
C. 10. D. 1.
7. : Khẳng định nào sau đây là đúng về phép tịnh tiến?
A. Phép tịnh tiến theo vectơ \(\overrightarrow v \) là điểm biến điểm \(M\) thành điểm \(M’\) thì \(\overrightarrow {M’M} = \overrightarrow v \).
B. Nếu \({T_{\overrightarrow v }}\left( M \right) = M’,\,{T_{\overrightarrow v }}\left( N \right) = N’\) thì \(MM’N’N\)là hình bình hành.
C. Phép tịnh tiến theo vectơ \(\overrightarrow v \) là phép đồng nhất nếu \(\overrightarrow v \) là vectơ \(\overrightarrow 0 \).
D. Phép tịnh tiến theo vectơ biến một đường thẳng thành một đường thẳng song song nó.
8. : Hình nào trong các hình sau không có trục đối xứng?
A.Hình tam giác đều.
B. Hình thoi.
C. Hình vuông.
D. Hình bình hành.
9. : Trong mặt phẳng \(\left( \alpha \right)\), cho bốn điểm \(A,\,B,\,C,\,D\)trong đó không có ba điểm nào thẳng hàng. Điểm \(S \notin \left( \alpha \right)\). Có mấy mặt phẳng tạo bởi \(S\) và hai trong bốn điểm nói trên?
A. 6. B. 4.
C. 5. D. 8.
1.0 : Tứ diện \(ABCD\). Phát biểu nào sau đây đúng?
A. Hai đường thẳng \(AC\) và \(BD\) cắt nhau.
B. Hai đường thẳng \(AC\) và \(BD\) không có điểm chung.
C. Tồn tại một mặt phẳng chứa hai đường thẳng\(AC\) và \(BD\).
D. Không thể vẽ hình biểu diễn tứ diện \(ABCD\) bằng các nét liền.
1.1 : Tìm tập nghiệm của phương trình \(\sin 3x + 1 = 0\)
A. \(\left\{ {\left. { – \dfrac{\pi }{2} + k\pi } \right|k \in Z} \right\}\).
B. \(\left\{ {\left. { – \dfrac{\pi }{2} + k2\pi } \right|k \in Z} \right\}\)
C. \(\left\{ {\left. { – \dfrac{\pi }{6} + k2\pi } \right|k \in Z} \right\}\).
D. \(\left\{ {\left. { – \dfrac{\pi }{6} + k\dfrac{{2\pi }}{3}} \right|k \in Z} \right\}\).
1.2 : Tìm các nghiệm của phương trình \({\sin ^2}x + \cos x – 1 = 0\) trong khoảng \(\left( {0;\pi } \right)\).
A. \(x = \dfrac{\pi }{2},\,x = 0,\,x = \pi \).
B. \(x = \dfrac{\pi }{4}\).
C. \(x = \dfrac{\pi }{4},\,\,x = \dfrac{\pi }{2}\).
D. \(x = \dfrac{\pi }{2}\).
1.3 : Giải phương trình \(\cos 2x = \sin \left( {x + \dfrac{\pi }{3}} \right)\).
A. \(\left\{ {\left. {\dfrac{\pi }{6} + k2\pi ,\, – \dfrac{\pi }{6} + k2\pi } \right|k \in Z} \right\}\).
B. \(\left\{ {\left. {\dfrac{\pi }{{18}} + \dfrac{{k2\pi }}{3},\, – \dfrac{\pi }{6} + \dfrac{{k2\pi }}{3}} \right|k \in Z} \right\}\).
C. \(\left\{ {\left. {\dfrac{\pi }{{18}} + \dfrac{{k2\pi }}{3},\, – \dfrac{\pi }{6} + k2\pi } \right|k \in Z} \right\}\).
D. \(\left\{ {\left. {\dfrac{\pi }{{18}} + \dfrac{{k2\pi }}{3},\, – \dfrac{\pi }{{18}} + \dfrac{{k2\pi }}{3}} \right|k \in Z} \right\}\).
1.4 : Tìm tập xác định của hàm số \(y = \dfrac{{\tan 2x}}{{1 – \tan \,x}}\).
A. \(R{\rm{\backslash }}\left\{ {\left. {\dfrac{\pi }{4} + k\pi } \right|k \in Z} \right\}\).
B. \(R{\rm{\backslash }}\left\{ {\left. {\dfrac{\pi }{4} + k\dfrac{\pi }{2},\,\dfrac{\pi }{2} + k\pi } \right|k \in Z} \right\}\).
C. \(R{\rm{\backslash }}\left\{ {\left. {\dfrac{\pi }{2} + k\pi } \right|k \in Z} \right\}\).
D. \(R{\rm{\backslash }}\left\{ {\left. {\dfrac{\pi }{4} + k\pi ,\,\dfrac{\pi }{2} + k\pi } \right|k \in Z} \right\}\).
1.5 : Tìm m để phương trình \(m\sin 2x + \left( {1 – m} \right)\cos 2x = \sqrt 5 \) có nghiệm.
A. \( – 1 < m < 2\).
B. \( – 1 \le m \le 2\).
C. \(m \le – 1\) hoặc \(m \ge 2\).
D. \(\forall m \in R\).
1.6 : Phương trình \(\sqrt 3 \sin 3x + \cos 3x = – 1\) tương đương với phương trình nào sau đây?
A. \(\sin \left( {3x + \dfrac{\pi }{6}} \right) = – \dfrac{1}{2}\).
B. \(\sin \left( {3x + \dfrac{\pi }{6}} \right) = – \dfrac{\pi }{6}\).
C. \(\sin \left( {3x – \dfrac{\pi }{6}} \right) = \dfrac{1}{2}\).
D. \(\sin \left( {3x + \dfrac{\pi }{6}} \right) = \dfrac{1}{2}\).
1.7 : Tìm số nghiệm của phương trình \(\tan \,x = 1\) trong khoảng \(\left( {0;7\pi } \right)\).
A. 5. B. 7.
C. 3. D. 4.
1.8 : Có bao nhiêu cách phân chia 8 học sinh thành hai nhóm sao cho một nhóm có 5 học sinh, nhóm còn lại có 3 học sinh?
Advertisements (Quảng cáo)
A. \(A_8^5\). B. \(C_8^3.C_8^5\).
C. \(C_8^5\). D. \(A_8^3.A_8^5\).
1.9 : Có bao nhiêu số tự nhiên có 5 chữ số, sao cho mỗi số đó, chữ số đứng sau lớn hơn số đứng trước.
A. \(A_9^5\). B. \(C_9^5\).
C. \(C_{10}^5\). D. \(A_{10}^5\).
2.0 : Tìm các giá trị của \(x\) thỏa mãn \(A_x^3 + C_x^{x – 3} = 14x\).
A. \(x = 5\).
B. \(x = 5\) hoặc \(x = – 2\).
C. \(x = – 2\).
D. Không tồn tại.
2.1 : Khai triển biểu thức \({\left( {x – {m^2}} \right)^4}\) ta được biểu thức nào trong các biểu thức dưới đây?
A. \({x^4} – 4{x^3}m + 6{x^2}{m^2} – 4x{m^3} + {m^4}\).
B. \({x^4} – {x^3}{m^2} + {x^2}{m^4} – x{m^6} + {m^8}\).
C. \({x^4} – 4{x^3}{m^2} + 6{x^2}{m^4} – 4x{m^6} + {m^8}\).
D. \({x^4} – {x^3}m + {x^2}{m^2} – x{m^3} + {m^4}\).
2.2 : Chọn ngẫu nhiên 5 sản phẩm trong 10 sản phẩm. Biết rằng trong 10 sản phẩm đó có 2 phế phẩm. Tính xác suất để trong sản phẩm được chọn không có phế phẩm nào.
A. \(\dfrac{1}{2}\). B. \(\dfrac{5}{8}\).
C. \(\dfrac{1}{5}\). D. \(\dfrac{2}{9}\).
2.3 : Một túi chứa 3 viên bi đỏ, 5 viên bi xanh và 6 viên bi vàng. Chọn ngẫu nhiên 3 viên bi. Tính xác suất để 3 viên bi được chọn không có đủ cả ba màu.
A. \(\dfrac{{137}}{{182}}\). B. \(\dfrac{{45}}{{182}}\).
C. \(\dfrac{1}{{120}}\). D. \(\dfrac{1}{{360}}\).
2.4 : Trong mặt phẳng với hệ trục tọa độ Oxy cho phép tịnh tiến theo vectơ \(\overrightarrow v = \left( {1; – 3} \right)\) biến điểm \(A\left( {4;5} \right)\) thành điểm \(A’\). Tìm tọa độ điểm \(A’\).
A. \(A’\left( {5;2} \right)\).
B. \(A’\left( {5; – 2} \right)\).
C. \(A’\left( { – 3; – 2} \right)\).
D. \(A’\left( {3;2} \right)\).
2.5 : Trong mặt phẳng, cho hai đường thẳng cắt nhau d và d’. Có bao nhiêu phép quay biến đường thẳng d thành đường thẳng d’?
A. 2. B. 0.
C. 1. D. Vô số.
2.6 : Trong mặt phẳng với hệ trục tọa độ Oxy cho điểm \(M\left( {3;2} \right)\). Tìm tọa độ điểm \(M’\)là ảnh của điểm M qua phép quay tâm O góc quay \({90^0}\).
A. \(M’\left( { – 2;3} \right)\).
B. \(M’\left( {2;3} \right)\).
C. \(M’\left( { – 2; – 3} \right)\).
D. \(M’\left( {2; – 3} \right)\).
2.7 : Mệnh đề nào sau đây sai?
A. Phép dời hình biến đường thẳng thành đường thẳng, biến tia thành tia, biến một đoạn thẳng thành đoạn thẳng có độ dài bằng nó.
B. Phép dời hình là một phép đồng dạng với tỉ số đồng dạng bằng 1.
C. Phép đồng dạng biến một tam giác thành một tam giác bằng nó, biến một đường tròn thành đường tròn có cùng bán kính.
D. Phép vị tự tâm O, tỉ số k biến một góc thành một góc có số đo bằng nó.
2.8 : Cho hình chóp S.ABCD, AB và CD cắt nhau tại I. Phát biểu nào sau đây đúng?
A. Giao tuyến của (SAB) và (SCD) là đường thẳng SI.
B. Giao tuyến của (SAC) và (SCD) là đường thẳng SI.
C. Giao tuyến của (SAB) và (SCD) là đường thẳng SK với K là giao điểm của SD và BC.
D. Giao tuyến của (SOC) và (SAD) là đường thẳng SM với M là giao điểm của AC và SD.
2.9 : Cho ba đường thẳng a, b, c đôi một cắt nhau và không đồng phẳng. Tìm số giao điểm phân biệt của ba đường thẳng đã cho.
A. 1. B. 3.
C. 6. D. 2.
3.0 : Cho hình chóp S.ABCD, đáy là hình bình hành ABCD, các điểm M và N lần lượt thuộc các cạnh AB, SC. Phát biểu nào sau đây đúng?
A. Giao điểm của MN với (SBD) là giao điểm của MN với BD.
B. Giao điểm của MN với (SBD) là điểm M.
C. Giao điểm của MN với (SBD) là giao điểm của MN với SI, trong đó I là giao của CM với BD.
Advertisements (Quảng cáo)
D. Đường thẳng MN không cắt mặt phẳng (SBD).
3.1 : Tìm tập nghiệm của phương trình \(\sin 3x – \cos x = 0\).
A. \(\left\{ {\left. {\dfrac{\pi }{8} + k\pi ,\,\,\dfrac{\pi }{4} + k2\pi } \right|k \in Z} \right\}\).
B. \(\left\{ {\left. {\dfrac{\pi }{8} + k\dfrac{\pi }{2}} \right|k \in Z} \right\}\).
C.\(\left\{ {\left. {\dfrac{\pi }{8} + k\dfrac{\pi }{2},\,\,\dfrac{\pi }{4} + k\pi } \right|k \in Z} \right\}\).
D. \(\left\{ {\left. {\dfrac{\pi }{4} + k\pi } \right|k \in Z} \right\}\).
3.2 : Tính tổng các nghiệm thuộc \(\left[ { – 2\pi ;2\pi } \right]\) của phương trình \({\sin ^2}x + \cos 2x + 2\cos x = 0\).
A. \(2\pi \). B. \(\dfrac{{2\pi }}{3}\)
C. \(\dfrac{\pi }{3}\). D. \(0\).
3.3 : Giải phương trình \({\cos ^2}x + \sin 2x – 3{\sin ^2}x = 0\).
A. \(\left\{ {\left. { – \dfrac{\pi }{4} + k\pi ;\,\,\arctan 3 + k\pi } \right|k \in Z} \right\}\).
B. \(\left\{ {\left. {\dfrac{\pi }{4} + k\dfrac{\pi }{2}} \right|k \in Z} \right\}\).
C. \(\left\{ {\left. {\dfrac{\pi }{4} + k\pi ;\,\,{\mathop{\rm arccot}\nolimits} \left( { – 3} \right) + k\pi } \right|k \in Z} \right\}\)
D. \(\left\{ {\left. { – \dfrac{\pi }{4} + k\pi ;\,\,\arctan \left( { – \dfrac{1}{3}} \right) + k\pi } \right|k \in Z} \right\}\).
3.4 : Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = 3 – \sqrt 2 \left( {\sin x + \cos x} \right)\). Tính tổng \(M + m\).
A. 5. B. 1.
C. 6. D. 4.
3.5 : Ban văn nghệ lớp 11A có 7 học sinh nam và 9 học sinh nữ. Cần chọn 5 học sinh nam và 5 học sinh nữ để ghép thành 5 cặp nam nữ trình diễn tiết mục thời trang. Hỏi có bao nhiêu cách chọn thỏa mãn yêu cầu bài toán?
A. 2446.
B. 38102400.
C. 317520.
D. 4572288000.
3.6 : Tìm hệ số của số hạng chứa \({x^4}\)trong khai triển nhị thức Niu-tơn của \({\left( {x + \dfrac{2}{{{x^2}}}} \right)^{10}}\), với \(x \ne 0\).
A. 85. B. 180.
C. 95. D. 108.
3.7 : Một thợ săn bắn 3 viên đạn vòa con mồi. Xác suất để bắn trúng mục tiêu là 0,4. Tính xác suất để người thợ săn bắn trượt mục tiêu.
A. 0,064. B. 0,784.
C. 0,216. D. 0,936.
3.8 : Trong mặt phẳng tọa độ Oxy, cho đường tròn \(\left( C \right):{\left( {x + 2} \right)^2} + {\left( {y – 5} \right)^2} = 16\). Tìm phương trình đường tròn \(\left( {C’} \right)\)là ảnh của đường tròn \(\left( C \right)\) qua phép tịnh tiến theo vectơ \(\overrightarrow v = \left( {2; – 7} \right)\).
A. \({x^2} + {\left( {y + 2} \right)^2} = 4\).
B. \({x^2} + {\left( {y + 2} \right)^2} = 16\).
C. \({\left( {x – 4} \right)^2} + {\left( {y + 2} \right)^2} = 16\).
D. \({\left( {x – 4} \right)^2} + {\left( {y – 12} \right)^2} = 16\).
3.9 : Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(d:\,x + y = 0\). Tìm phương trình đường thẳng \(d’\) là ảnh của đường thẳng d qua phép quay \(Q\left( {O; – {{90}^0}} \right)\).
A. \(x – y + 1 = 0\).
B. \(x – y – 1 = 0\).
C. \(x – y = 0\).
D. \(x – 90y = 0\).
4.0 : Cho tam giác ABC với trọng tâm G. Gọi \(A’,\,B’,C’\)lần lượt là trung điểm của các cạnh BC, CA, AB. Khi đó phép vị tự nào biến tam giác \(A’B’C’\)thành tam giác ABC ?
A. Phép vị tự tâm G, tỉ số 2.
B. Phép vị tự tâm G, tỉ số \( – \dfrac{1}{2}\).
C. Phép vị tự tâm G, tỉ số \(\dfrac{1}{2}\).
D. Phép vị tự tâm G, tỉ số \( – 2\).
B. PHẦN RIÊNG (20%, gồm 10 câu)
1. Phần dành cho học sinh không chuyên
4.1 : Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm \(M\left( {1;4} \right),\,M’\left( { – 3; – 12} \right)\). Phép vị tự tâm I, tỉ số \( – 3\) biến điểm \(M\) thành điểm \(M’\). Tìm tọa độ điểm \(I\).
A. \(\left( {0;0} \right)\). B. \(\left( { – 3; – 3} \right)\).
C. \(\left( { – 3;0} \right)\). D. \(\left( {0; – 3} \right)\).
4.2 : Cho hình chóp \(O.ABC\), \(A’\)là trung điểm của OA, B’, C’ lần lượt thuộc các cạnh OB, OC và không phải là trung điểm của các cạnh này. Phát biểu nào sau đây sai?
A. Mặt phẳng (ABC) và mặt phẳng (A’B’C’) không có điểm chung.
B. Đường thẳng OA và B’C’ không cắt nhau.
C. Đường thẳng AC và A’C’ cắt nhau tại một điểm thuộc mặt phẳng (ABC).
D. Đường thẳng AB và A’B’ cắt nhau tại một điểm thuộc mặt phẳng (ABC).
4.3 : Cho hình chóp S.ABCD, M là điểm nằm trong tam giác SAB. Phát biểu nào sau đây đúng?
A. Giao điểm của (SCM) với BD là giao điểm của CN với BD, trong đó N là giao điểm của SM với AB.
B. Giao điểm của (SCM) với BD là giao điểm của CM với BD.
C. Giao điểm của (SAD) với CM là giao điểm của SA với CM.
D. Đường thẳng DM không cắt mặt phẳng (SAC).
4.4 : Cho phương trình \(\cos \left( {\pi \cos 2x} \right) = 1\). Tập hợp nào trong các tập hợp được liệt kê ở các phương án A, B, C, D dưới đây, không là tập nghiệm của phương trình đã cho?
A. \(\left\{ {\left. {\dfrac{\pi }{4} – k\dfrac{\pi }{2}} \right|k \in Z} \right\}\).
B. \(\left\{ {\left. {\dfrac{\pi }{4} + k\pi } \right|k \in Z} \right\}\).
C. \(\left\{ {\left. {\dfrac{{3\pi }}{4} + k\dfrac{\pi }{2}} \right|k \in Z} \right\}\).
D. \(\left\{ {\left. {{\pi \over 4} + k{\pi \over 2}} \right|k \in Z} \right\}\)
4.5 : Tìm các giá trị của m để phương trình \(\sin 2x + 4\left( {\cos x – \sin \,x} \right) = m\) có nghiệm.
A. \( – 1 – 4\sqrt 2 \le m < 0\).
B. \(0 < m \le 1 + 4\sqrt 2 \).
C. \( – 1 – 4\sqrt 2 \le m \le – 1 + 4\sqrt 2 \).
D. \(m > 1 + 4\sqrt 2 \).
4.6 : Tính giá trị biểu thức \(M = {2^{2016}}C_{2017}^1 + {2^{2014}}C_{2017}^3 \)\(\,+ {2^{2012}}C_{2017}^5 + … + {2^0}C_{2017}^{2017}\).
A. \(\dfrac{1}{2}\left( {{3^{2107}} – 1} \right)\).
B. \(\dfrac{1}{2}\left( {{3^{2107}} + 1} \right)\).
C. \(\dfrac{1}{2}\left( {{2^{2107}} – 1} \right)\).
D. \(\dfrac{1}{2}\left( {{2^{2107}} + 1} \right)\).
4.7 : Có bao nhiêu cách xếp 5 bạn nữ và 3 bạn nam thành một hàng ngang sao cho không có 2 bạn nam nào đứng cạnh nhau?
A. \(8! – 3.3!\). B. \(8! – 3!\).
C. \(14400\). D. \(14396\).
4.8 : Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng \(d:x + 2y – 1 = 0\) và \(d’:x + 2y – 5 = 0\). Phép tịnh tiến theo vectơ \(\overrightarrow u \) biến đường thẳng d thành đường thẳng d’. Khi đó, độ dài bé nhất của vectơ \(\overrightarrow u \) là bao nhiêu?
A. \(\dfrac{{4\sqrt 5 }}{5}\)
B. \(\dfrac{{2\sqrt 5 }}{5}\).
C. \(\dfrac{{3\sqrt 5 }}{5}\).
D. \(\dfrac{{\sqrt 5 }}{5}\).
4.9 : Cho tam giác ABC nội tiếp đường tròn \(\left( O \right)\) có bán kính \(R = 9\,cm\). Hai điểm B, C cố định, I là trung điểm của BC, G là trọng tâm tam giác ABC. Biết rẳng khi A di động trên \(\left( O \right)\) thì G di động trên một đường tròn \(\left( {O’} \right)\). Tính bán kính R’ của đường tròn \(\left( {O’} \right)\).
A. \(R’ = 3cm\).
B. \(R’ = 4cm\).
C. \(R’ = 2cm\).
D. \(R’ = 6cm\).
5.0 : Cho hình chóp \(S.ABCD\), \(A’\)là trung điểm của \(SA\), \(B’\) là điểm thuộc cạnh \(SB\). Phát biểu nào sau đây đúng?
A. Thiết diện của hình chóp \(S.ABCD\)cắt bởi mặt phẳng \(\left( {A’B’C} \right)\) chỉ có thể là tam giác.
B. Thiết diện của hình chóp \(S.ABCD\)cắt bởi mặt phẳng \(\left( {A’B’C} \right)\) chỉ có thể là tứ giác.
C. Thiết diện của hình chóp \(S.ABCD\)cắt bởi mặt phẳng \(\left( {A’B’C} \right)\) chỉ có thể là tứ giác hoặc tam giác.
D. Thiết diện của hình chóp \(S.ABCD\)cắt bởi mặt phẳng \(\left( {A’B’C} \right)\) chỉ có thể là tứ giác hoặc ngũ giác.
2. Phần dành cho học sinh chuyên
5.1 : Cho hàm số \(y = \dfrac{{m\cos x + m – 1}}{{\sin \,x + \cos x + 3}}\). Tìm m để \(y < 1,\,\,\forall x \in R\).
A. \(m < 0\).
B. \(\dfrac{7}{3} \le m \le 5\).
C. \(m < \dfrac{7}{3}\).
D. \(0 < m < \dfrac{7}{3}\).
5.2 : Tìm chu kỳ của hàm số \(y = \sin \,x.\cos \dfrac{{3x}}{2}\).
A. \(2\pi \). B. \(6\pi \).
C. \(4\pi \). D. \(8\pi \).
5.3 : Tính tổng \(S = \sum\limits_{k = 0}^{1983} {C_{2017 + k}^k} \).
A. \(C_{4001}^{2017}\). B. \(C_{4001}^{2018}\).
C. \(C_{4002}^{2017}\). D. \(C_{6017}^{4000}\).
5.4 : Lấy ngẫu nhiên 3 số tự nhiên đôi một khác nhau, có hai chữ số và cộng cả 3 số lại. Tính xác suất để tổng nhận được chia hết cho 3.
A. \(\dfrac{{203}}{{1958}}\).
B. \(\dfrac{{653}}{{1958}}\).
C. \(\dfrac{{225}}{{979}}\).
D. \(\dfrac{{124}}{{979}}\).
5.5 : Có bao nhiêu cách chia 20 viên bi giống hệt nhay vào 4 cái hộp đôi một khác nhau, sao cho mỗi cái hộp có ít nhất 2 viên bi.
A. \(C_{20}^4\). B. \(C_{19}^3\).
C. \(C_{12}^4\). D. \(C_{15}^3\).
5.6 : Cho tứ giác đều ABCD có cạnh bằng a, lấy điểm E đối xứng với B qua C, điểm F đối xứng với B qua D. Gọi M là trung điểm của AB. Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng (MEF).
A. \(\dfrac{{{a^2}}}{4}\). B. \(\dfrac{{{a^2}}}{6}\).
C. \(\dfrac{{{a^2}\sqrt 3 }}{9}\). D. \(\dfrac{{{a^2}\sqrt 3 }}{{12}}\).
5.7 : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. M là trung điểm của SB và G là trọng tâm tam giác SAD. Gọi J là giao điểm của AD và mặt phẳng (OMG). Tính tỉ số \(\dfrac{{JA}}{{JD}}\).
A. \(1\). B. \(\dfrac{1}{2}\).
C. 2. D. \(\dfrac{5}{3}\).
5.8 : Trong mặt phẳng Oxy, cho phép biến hình F biết với điểm \(M\left( {x;y} \right)\) thì ảnh của M qua phép biến hình F là điểm \(M’\left( {2x – y;3x – 2y} \right)\). Phát biểu nào về tập hợp các điểm I thỏa mãn \(F\left( I \right) = I\) sau đây là đúng?
A. Tập hợp điểm I là một điểm.
B. Tập hợp điểm I là một đường tròn.
C. Tập hợp điểm I là một đường thẳng.
D. Tập hợp điểm I là hai đường thẳng cắt nhau.
5.9 : Cho hình bình hành ABCD, E là hình chiếu của B trên CD và K là hình chiếu của B trên AD, \(KE = 3\) và \(BD = 5\). Tính khoảng cách từ \(B\)đến trực tâm của tam giác BEK.
A. 4. B. 5.
C. \(\dfrac{9}{2}\). D. \(2\sqrt 3 \).
6.0 : Trong mặt phẳng Oxy, cho các điểm \(A\left( {1;2} \right),\,B\left( {4;5} \right),\,C\left( { – 1;4} \right)\). Phép vị tự tâm \(I\left( {3;2} \right)\), tỉ số \(k = 3\) biến tam giác ABC thành tam giác A’B’C’. Tính diện tích tam giác A’B’C’.
A. 27. B. 108.
C. \(36\sqrt 2 \). D. 54.

|
Phần chung |
|||
|
1. B |
11. D |
21. C |
31. C |
|
2. C |
12. D |
22. D |
32. D |
|
3. C |
13. C |
23. A |
33. C |
|
4. B |
14. B |
24. A |
34. C |
|
5. D |
15. C |
25. D |
35. C |
|
6. B |
16. A |
26. A |
36. B |
|
7. C |
17. B |
27. C |
37. C |
|
8. D |
18. C |
28. A |
38. B |
|
9. A |
19. B |
29. B |
39. C |
|
10. B |
20. A |
30. C |
40. D |
|
Phần riêng |
|
|
Không chuyên |
Chuyên |
|
41. A |
51. C |
|
42. A |
52. C |
|
43. A |
53. B |
|
44. B |
54. B |
|
45. C |
55. D |
|
46. A |
56. B |
|
47. C |
57. C |
|
48. A |
58. C |
|
49. A |
59. A |
|
50. C |
60. D |


![Kiểm tra học kì 2 [Toán lớp 11]: Trong các giới hạn sau đây, giới hạn nào là 0?](https://dethikiemtra.com/wp-content/uploads/2019/04/toan-lop-11-1-100x75.jpg)



