
Phần I: Trắc nghiệm (2,0đ)
1. : Tập xác định của hàm số \(y = \dfrac{{3x – 1}}{{x – 2}} + 4\sqrt {2 – x} \) là:
A. \(\left( { – \infty ;2} \right)\)
B. \(\left( { – \infty ;2} \right]\)
C. \(\left[ {2; + \infty } \right)\)
D. \(\left( {2; + \infty } \right)\)
2. : Cho hàm số \(y = – 2{x^2} + 4x + 1\). Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên \(\left( {1; + \infty } \right)\)
B. Hàm số đồng biến trên \(\left( { – \infty ;1} \right)\)
C. Hàm số nghịch biến trên \(\left( {3; + \infty } \right)\)
D. Hàm số đồng biến trên \(\left( { – \infty ;3} \right)\)
3. : Để hai đồ thị hàm số \(y = – {x^2} – 4x\) và \(y = {x^2} – m\) có hai điểm chung thì:
A. \(m \ge – 2\) B. \(m > – 2\)
C. \(m \le – 2\) D. \(m < – 2\)
4. : Phương trình \(\left( {m – 2} \right){x^2} – 2x – 1 = 0\) có nghiệm khi:
A. \(m \ge – 1\) B. \(m \le – 1\)
C. \(m \ge 1\) D. \(m \le 1\)
5. : Phương trình \(\left( {{x^2} – 3x + 2} \right)\sqrt {x – 3} = 0\) có bao nhiêu nghiệm?
A. 0 B. 1
C. 2 D. 3
6. : Cho tam giác ABC đều cạnh bằng a, nội tiếp đường tròn tâm O. Khi đó \(\overrightarrow {AO} .\overrightarrow {OB} \) bằng:
A. \(\dfrac{{{a^2}}}{6}\)
B. \( – \dfrac{{{a^2}}}{6}\)
C. \(\dfrac{{{a^2}}}{{2\sqrt 3 }}\)
D. \( – \dfrac{{{a^2}}}{{2\sqrt 3 }}\)
7. : Trong mặt phẳng hệ tọa độ Oxy, cho hình bình hành ABCD biết \(A\left( {1; – 5} \right);\,\,B\left( {2;3} \right);\,\,C\left( { – 3;3} \right)\). Tọa độ tâm I của hình bình hành là:
A. \(\left( {1;1} \right)\)
Advertisements (Quảng cáo)
B. \(\left( { – 1;1} \right)\)
C. \(\left( {1; – 1} \right)\)
D. \(\left( { – 1; – 1} \right)\)
8. : Cho \(\sin x = \dfrac{3}{5},\,\,{90^0} < x < {180^0}\). Giá trị của biểu thức \(P = \tan x.{\cos ^2}x\) bằng:
A. \(\dfrac{{12}}{{25}}\) B. \(\dfrac{{25}}{{12}}\)
C. \( – \dfrac{{25}}{{12}}\) D. \( – \dfrac{{12}}{{25}}\)
Phần II. Tự luận (8đ)
1. (1,5đ) Tìm tất cả các giá trị của m để phương trình \({x^2} – \left( {2m + 1} \right)x + {m^2} + 2 = 0\) có hai nghiệm \({x_1};{x_2}\) phân biệt sao cho \({x_1}\left( {{x_2} – 2{x_1}} \right) + {x_2}\left( {{x_1} – 2{x_2}} \right) + 14 = 0\).
2. (2,5đ) Giải các phương trình sau:
a) \(\left( {3x – 8} \right)\left| {11 – 3x} \right| = 3{x^2} – 17x + 24\) b) \(\sqrt {2x – 1} + \sqrt {x – 1} + 22 = 3x + 2\sqrt {2{x^2} – 3x + 1} \)
3. (1,5đ) Cho hình thang cân ABCD, biết \(CD = 3AB = 3a\) và \(\widehat {ADC} = {45^0}\). AH vuông góc với CD tại H. Tính các vô hướng \(\overrightarrow {AH} .\left( {2\overrightarrow {AD} – 3\overrightarrow {CD} } \right);\,\,\overrightarrow {AC} .\overrightarrow {BH} \).
4. (1,5đ) Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC biết \(A\left( {1;1} \right);\,\,B\left( {0;4} \right);\,\,C\left( { – 4;2} \right)\).
a) Trên đường thẳng BC lấy điểm M sao cho \(\overrightarrow {BM} = k\overrightarrow {BC} \). Tìm k để tam giác ACM cân tại M.
b) Tìm điểm D thuộc trục Oy sao cho góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \) bằng 450
5. (1,0đ) Tìm tất cả các giá trị của m để phương trình \(\left( {{x^2} + 4x + 3} \right)\left( {{x^2} + 8x + 14} \right) – m + 2017 = 0\) có nghiệm thỏa mãn \({x^2} + 6x + 6 \le 0\).

Phần I: Trắc nghiệm (2,0đ)
Advertisements (Quảng cáo)
|
1. A |
2. B |
3. B |
4. C |
5. B |
|
6. A |
7. D |
8. D |
|
|
Phần II. Tự luận (8đ)
1. Để phương trình có 2 nghiệm phân biệt \({x_1};{x_2}\)\( \Leftrightarrow \Delta > 0\)
\( \Leftrightarrow {\left( {2m + 1} \right)^2} – 4\left( {{m^2} + 2} \right) > 0\)
\(\Leftrightarrow 4{m^2} + 4m + 1 – 4{m^2} – 8 > 0 \)
\(\Leftrightarrow 4m – 7 > 0 \Leftrightarrow m > \dfrac{7}{4}\).
Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m + 1\\{x_1}{x_2} = {m^2} + 2\end{array} \right.\)
\(\begin{array}{l}\,\,\,\,\,{x_1}\left( {{x_2} – 2{x_1}} \right) + {x_2}\left( {{x_1} – 2{x_2}} \right) + 14 = 0\\ \Leftrightarrow {x_1}{x_2} – 2x_1^2 + {x_1}{x_2} – 2x_2^2 + 14 = 0\\ \Leftrightarrow 2{x_1}{x_2} – 2\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} – 2{x_1}{x_2}} \right] + 14 = 0\\ \Leftrightarrow – 2{\left( {{x_1} + {x_2}} \right)^2} + 6{x_1}{x_2} + 14 = 0\\ \Leftrightarrow – 2{\left( {2m + 1} \right)^2} + 6\left( {{m^2} + 2} \right) + 14 = 0\\ \Leftrightarrow – 8{m^2} – 8m – 2 + 6{m^2} + 12 + 14 = 0\\ \Leftrightarrow – 2{m^2} – 8m + 24 = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 2\,\,\,\,\,\,\left( {tm} \right)\\m = – 6\,\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy \(m = 2.\)
2. a) \(\eqalign{
& a)\,\,\left( {3x – 8} \right)\left| {11 – 3x} \right| = 3{x^2} – 17x + 24 \cr
& \Leftrightarrow \left( {3x – 8} \right)\left| {11 – 3x} \right| = \left( {x – 3} \right)\left( {3x – 8} \right) \cr
& \Leftrightarrow \left( {3x – 8} \right)\left[ {\left| {11 – 3x} \right| – x + 3} \right] = 0 \cr
& \Leftrightarrow \left[ \matrix{
3x – 8 = 0 \hfill \cr
\left| {11 – 3x} \right| – x + 3 = 0 \hfill \cr} \right. \cr
& \Leftrightarrow \left[ \matrix{
x = {8 \over 3} \hfill \cr
\left| {11 – 3x} \right| = x – 3 \hfill \cr} \right. \cr
& \Leftrightarrow \left[ \matrix{
x = {8 \over 3} \hfill \cr
\left\{ \matrix{
x \ge 3 \hfill \cr
9{x^2} – 66x + 121 = {x^2} – 6x + 9 \hfill \cr} \right. \hfill \cr} \right. \cr
& \Leftrightarrow \left[ \matrix{
x = {8 \over 3} \hfill \cr
\left\{ \matrix{
x \ge 3 \hfill \cr
8{x^2} – 60x + 112 = 0 \hfill \cr} \right. \hfill \cr} \right. \cr
& \Leftrightarrow \left[ \matrix{
x = {8 \over 3} \hfill \cr
\left\{ \matrix{
x \ge 3 \hfill \cr
\left[ \matrix{
x = 4 \hfill \cr
x = {7 \over 2} \hfill \cr} \right. \hfill \cr} \right. \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
x = {8 \over 3} \hfill \cr
x = 4 \hfill \cr
x = {7 \over 2} \hfill \cr} \right. \cr} \)
Vậy tập nghiệm của phương trình là \(S = \left\{ {\dfrac{8 }{ 3};4;\dfrac{7}{ 2}} \right\}\)
b) \(\sqrt {2x – 1} + \sqrt {x – 1} + 22 = 3x + 2\sqrt {2{x^2} – 3x + 1} \)
ĐKXĐ: \(\left\{ \begin{array}{l}2x – 1 \ge 0\\x – 1 \ge 0\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}x \ge \dfrac{1}{2}\\x \ge 1\end{array} \right. \Leftrightarrow x \ge 1\).
Đặt \(t = \sqrt {2x – 1} + \sqrt {x – 1} \,\,\left( {t \ge 0} \right)\) ta có: \({t^2} = 2x – 1 + x – 1 + 2\sqrt {\left( {2x – 1} \right)\left( {x – 1} \right)} = 3x – 2 + 2\sqrt {2{x^2} – 3x + 1} \)
\( \Rightarrow 3x + 2\sqrt {2{x^2} – 3x + 1} = {t^2} + 2\)
Khi đó phương trình trở thành \(t + 22 = {t^2} + 2\)
\(\Leftrightarrow {t^2} – t – 20 = 0\)
\(\Leftrightarrow \left[ \begin{array}{l}t = 5\,\,\,\,\,\,\,\left( {tm} \right)\\t = – 4\,\,\,\left( {ktm} \right)\end{array} \right.\)
\(\begin{array}{l}t = 5 \Rightarrow 3x + 2\sqrt {2{x^2} – 3x + 1} = 27 \\\Leftrightarrow 2\sqrt {2{x^2} – 3x + 1} = 27 – 3x\\ \Leftrightarrow \left\{ \begin{array}{l}27 – 3x \ge 0\\4\left( {2{x^2} – 3x + 1} \right) = 9{x^2} – 162x + 729\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \le 9\\{x^2} – 150x + 725 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \le 9\\\left[ \begin{array}{l}x = 5\\x = 145\end{array} \right.\end{array} \right.\\ \Leftrightarrow x = 5\,\,\left( {tm\,\,ĐKXĐ} \right)\end{array}\)
Vậy phương trình có nghiệm \(x = 5.\)
3.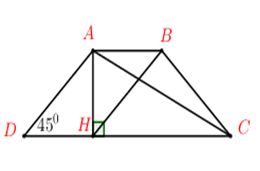
\( + )\,\,\overrightarrow {AH} .\left( {2\overrightarrow {AD} – 3\overrightarrow {CD} } \right) = 2\overrightarrow {AH} .\overrightarrow {AD} – 3\overrightarrow {AH} .\overrightarrow {CD} = 2AH.AD.\cos \widehat {HAD}\).
Ta có: \(\Delta AHD\) có \(\widehat {ADH} = {45^0} \Rightarrow \Delta AHD\) vuông cân tại H.
Ta có: và \(\widehat {HAD} = {45^0}\)
\( \Rightarrow \overrightarrow {AH} \left( {2\overrightarrow {AD} – 3\overrightarrow {CD} } \right) = 2.a.a\sqrt 2 .\cos {45^0} = 2{a^2}\sqrt 2 .\dfrac{{\sqrt 2 }}{2} = 2{a^2}\)
\(\begin{array}{l} + )\,\,\overrightarrow {AC} .\overrightarrow {BH} = \left( {\overrightarrow {AH} + \overrightarrow {HC} } \right)\left( {\overrightarrow {AH} – \overrightarrow {AB} } \right) = A{H^2} – \underbrace {\overrightarrow {AB} .\overrightarrow {AH} }_0 + \underbrace {\overrightarrow {AH} .\overrightarrow {HC} }_0 – \overrightarrow {AB} .\overrightarrow {HC} \\ = A{H^2} – \overrightarrow {AB} .\overrightarrow {HC} = A{B^2} – AB.HC.\cos 0 = A{B^2} – AB.HC\\ = {a^2} – a.2a = – {a^2}\end{array}\)
4. a) Gọi \(M\left( {a;b} \right)\) ta có: \(\overrightarrow {BM} = \left( {a;b – 4} \right);\,\,\overrightarrow {BC} = \left( { – 4; – 2} \right)\)
\(\overrightarrow {BM} = k\overrightarrow {BC} \Rightarrow \left\{ \begin{array}{l}a = – 4k\\b – 4 = – 2k\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = – 4k\\b = – 2k + 4\end{array} \right. \Rightarrow M\left( { – 4k; – 2k + 4} \right)\)
Để tam giác ACM cân tại M thì \(MA = MC \Leftrightarrow M{A^2} = M{C^2}\)
\(\begin{array}{l} \Leftrightarrow {\left( { – 4k – 1} \right)^2} + {\left( { – 2k + 3} \right)^2} = {\left( { – 4k + 4} \right)^2} + {\left( { – 2k + 2} \right)^2}\\ \Leftrightarrow 8k + 1 – 12k + 9 = – 32k + 16 – 8k + 4\\ \Leftrightarrow 36k = 10 \Leftrightarrow k = \dfrac{5}{{18}}\\ \Rightarrow M\left( { – \dfrac{{10}}{9};\dfrac{{31}}{9}} \right)\end{array}\)
Vậy \(M\left( { – \dfrac{{10}}{9};\dfrac{{31}}{9}} \right)\).
b) Gọi \(D\left( {0;d} \right) \in Oy\). Ta có: \(\overrightarrow {AB} = \left( { – 1;3} \right);\,\,\overrightarrow {AD} = \left( { – 1;d – 1} \right)\)
\(\begin{array}{l} \Rightarrow \cos \left( {\overrightarrow {AB} ;\overrightarrow {AD} } \right) = \dfrac{{\overrightarrow {AB} .\overrightarrow {AD} }}{{AB.AD}} = \dfrac{{1 + 3d – 3}}{{\sqrt {10} \sqrt {1 + {{\left( {d – 1} \right)}^2}} }} = \dfrac{{3d – 2}}{{\sqrt {10} \sqrt {{d^2} – 2d + 2} }}\\ \Rightarrow \dfrac{1}{{\sqrt 2 }} = \dfrac{{3d – 2}}{{\sqrt {10} \sqrt {{d^2} – 2d + 2} }}\\ \Leftrightarrow \sqrt 5 \sqrt {{d^2} – 2d + 2} = 3d – 2\\ \Leftrightarrow \left\{ \begin{array}{l}3d – 2 \ge 0\\5{d^2} – 10d + 10 = 9{d^2} – 12d + 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}d \ge \dfrac{2}{3}\\\left[ \begin{array}{l}d = \dfrac{3}{2}\,\\d = – 1\end{array} \right.\end{array} \right.\\ \Rightarrow d = \dfrac{3}{2} \Rightarrow D\left( {0;\dfrac{3}{2}} \right)\end{array}\)
Vậy \(D\left( {0;\dfrac{3}{2}} \right)\).
5. \(\begin{array}{l}\left( {{x^2} + 4x + 3} \right)\left( {{x^2} + 8x + 14} \right) – m + 2017 = 0\\ \Leftrightarrow \left( {{x^2} + 6x + 9 – 2x – 6} \right)\left( {{x^2} + 6x + 9 + 2x + 6} \right) – m + 2017 = 0\\ \Leftrightarrow {\left( {{x^2} + 6x + 9} \right)^2} – {\left( {2x + 6} \right)^2} – m + 2017 = 0\\ \Leftrightarrow {\left( {x + 3} \right)^4} – 4{\left( {x + 3} \right)^2} – m + 2017 = 0\end{array}\)
Đặt \(t = {\left( {x + 3} \right)^2} \ge 0\), khi đó phương trình trở thành \({t^2} – 4t – m + 2017 = 0 \)\(\,\Leftrightarrow {t^2} – 4t + 2017 = m\).
Ta có: \({x^2} + 6x + 6 \le 0 \)
\(\Leftrightarrow {x^2} + 6x + 9 \le 3 \)
\(\Leftrightarrow {\left( {x + 3} \right)^2} \le 3 \Leftrightarrow t \le 3\)
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(f\left( t \right) = {t^2} – 4t + 2017\,\,\left( {0 \le t \le 3} \right)\) và đường thẳng \(y = m\) song song với trục hoành.
Xét hàm số \(f\left( t \right) = {t^2} – 4t + 2017\,\,\left( {t \le 3} \right)\) ta có BBT :

Dựa vào BBT ta có : để phương trình có nghiệm \(t \in \left[ {0;3} \right]\) thì \(2013 \le m \le 2017\).
Vậy \(m \in \left[ {2013;2017} \right]\).





