Xác định khoảng đồng biến, khoảng nghịch biến và lập bảng biến thiên của hàm số?; Cho hai tập hợp \(\left( {1;3} \right)\) và \(\left[ {2;4} \right]\). Giao của hai tập hợp đã cho là gì? … trong Đề thi học kì 1 lớp 10 môn Toán. Xem Đề và đáp án đầy đủ phía dưới đây

PHẦN 1. TRẮC NGHIỆM (3đ)
1. : Cho hai tập hợp \(\left( {1;3} \right)\) và \(\left[ {2;4} \right]\). Giao của hai tập hợp đã cho là:
A. \(\left( {2;3} \right]\). B. \(\left( {2;3} \right)\).
C. \(\left[ {2;3} \right)\). D. \(\left[ {2;3} \right]\).
2. : Cho hàm số \(y = \left( {m – 1} \right)x + m – 2\). Điều kiện để hàm số đồng biến trên R là:
A. \(m < 2\). B. \(m > 1\).
C. \(m < 1\). D. \(m > 2\).
3. : Cho parabol\(y = 2{x^2} + 4x – 3\). Tọa độ đỉnh của parabol là:
A. \(\left( { – 1; – 5} \right)\). B. \(\left( {1;3} \right)\).
C. \(\left( {2;5} \right)\). D. \(\left( { – 2;5} \right)\).
4. : Điều kiện để đồ thị hàm số \(y = {x^2} – 4x + m\) cắt Ox tại hai điểm phân biệt là:
A. \(m < – 4\). B. \(m > 4\).
C. \(m > – 4\). D. \(m < 4\).
5. : Cho hàm số \(y = \sqrt {2 – x} + \dfrac{x}{{x – 1}}\). Tập xác định của hàm số là:
A. \(\left( { – \infty ;2} \right]\). B. \(\left[ {1;2} \right]\).
C. \(\left( { – \infty ;2} \right]{\rm{\backslash }}\left\{ 1 \right\}\). D. \(\left[ {2; + \infty } \right)\).
6. : Tập nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x – 3 \le 1 + 2x\\\dfrac{{x – 1}}{2} < 1\end{array} \right.\) là:
A. \(\left[ { – 4;3} \right)\). B. \(\left[ { – 4;3} \right]\).
C. \(\left( { – 4;3} \right)\). D. \(\left( { – 4;3} \right]\).
7. : Trên mặt phẳng tọa độ cho tam giác \(MNP\) có \(M\left( { – 2;1} \right),\,N\left( {1;3} \right),\,P\left( {0;2} \right)\). Tọa độ trọng tâm \(G\) của tam giác \(MNP\) là:
A. \(\left( {2;1} \right)\).
B. \(\left( {2; – \dfrac{1}{3}} \right)\).
C. \(\left( {1;2} \right)\).
D. \(\left( { – \dfrac{1}{3};2} \right)\).
8. : Trên mặt phẳng tọa độ cho \(\overrightarrow a = \left( {1; – 3} \right)\) và \(\overrightarrow b = \left( {2; – 1} \right)\). Giá trị của \(\overrightarrow a .\overrightarrow b \) bằng:
A. 6. B. 0.
C. 5. D. -1.
9. : Cho tam giác \(ABC\) có \(BC = a,\,CA = b,\,AB = c\). Biểu thức \({a^2} + {b^2} – {c^2}\) bằng:
A. \( – 2ab\cos C\).
B. \( – 2bc\cos A\).
C. \(2bc\cos A\).
D. \(2ab\cos C\).
1.0 : Cho góc \(\alpha \) thỏa mãn \(\cos \alpha = \dfrac{3}{5}\). Giá trị của \(\cos \left( {{{180}^0} – \alpha } \right)\) là:
A. \(\dfrac{3}{5}\). B. \( – \dfrac{3}{5}\).
Advertisements (Quảng cáo)
C. \(\dfrac{4}{5}\). D. \( – \dfrac{4}{5}\).
1.1 : Cho ba điểm \(A,\,B,\,C\) phân biệt và thẳng hàng, trong đó \(C\) nằm giữa \(A\) và \(B\). Xét các khẳng định sau
i) \(\overrightarrow {AB} ,\,\,\overrightarrow {AC} \) là hai vectơ cùng hướng.
ii) \(\overrightarrow {AB} ,\,\,\overrightarrow {AC} \) là hai vectơ ngược hướng.
iii) \(\overrightarrow {CB} ,\,\,\overrightarrow {AC} \) là hai vectơ cùng hướng.
iv) \(\overrightarrow {CB} ,\,\,\overrightarrow {AC} \) là hai vectơ ngược hướng.
Số khẳng định đúng là:
A. 3. B. 2.
C. 1. D. 0.
1.2 : Cho hình bình hành \(ABCD\). Xét các khẳng định sau
\(i)\,\overrightarrow {AB} = \,\overrightarrow {CD} \).
\(ii)\,\overrightarrow {AC} = \,\overrightarrow {BD} \).
\(iii)\,\overrightarrow {AD} = \,\overrightarrow {CB} \).
\(iv)\,\overrightarrow {AC} = \,\overrightarrow {AD} – \,\overrightarrow {BA} \).
Số khẳng định đúng là:
A. 0. B. 1.
C. 2. D. 3.
PHẦN 2. TỰ LUẬN (7đ)
Bài 1 . (1,5đ) Cho parabol \(\left( P \right):\,\,y = {x^2} + 2x – 3\)
a) Xác định trục đối xứng và tọa độ đỉnh của parabol \(\left( P \right)\). Vẽ parabol \(\left( P \right)\).
b) Xác định khoảng đồng biến, khoảng nghịch biến và lập bảng biến thiên của hàm số \(y = {x^2} + 2x – 3\).
Bài 2 . (2đ) a) Giải phương trình \(\sqrt {2x + 9} = x – 3\)
Advertisements (Quảng cáo)
b) Trong các đợt ủng hộ các bạn học sinh ở vùng bị bão lụt, các bạn học sinh lớp 10A đã quyên góp được \(1\,200\,000\). Mỗi em chỉ quyên góp bằng các tờ tiền \(2000,\,\,5000,\,\,10\,000\). Tổng số tiền loại \(2000\)và số tiền loại \(5000\) bằng số tiền loại \(10\,000\). Số tiền loại \(2000\) nhiều hơn số tiền loại \(5000\) là \(200\,000\). Hỏi có bao nhiêu số tiền mỗi loại?
Bài 3 . (3đ) a) Cho tam giác nhọn \(ABC\), \(AB = 2a,\,AC = 3a,\,\,\widehat {BAC} = {60^0}\). Về phía ngoài tam giác, dựng tam giác \(ACD\) vuông cân tại đỉnh \(A\). Tính độ dài các đoạn thẳng \(BC,\,BD\) và các tích vô hướng \(\overrightarrow {AB} .\,\overrightarrow {AC} ,\,\,\overrightarrow {BD} .\,\overrightarrow {AC} \) theo \(a\).
b) Trong mặt phẳng với hệ tọa độ \(Oxy\), cho tam giác \(ABC\) có ba đỉnh \(A\left( {1;2} \right),\,B\left( { – 1; – 1} \right),\,C\left( {2; – 1} \right)\). Tìm tọa độ trực tâm \(H\) của tam giác \(ABC\).
Bài 4 . (0,5đ) Giải phương trình \(\sqrt {x – \sqrt {2x – 1} } + \sqrt {x + 4 – 3\sqrt {2x – 1} } = \sqrt 2 \).

PHẦN 1. TRẮC NGHIỆM (3đ)
|
1.. C |
2.. B |
3.. A |
4.. D |
5.. C |
|
6.. A |
7.. D |
8.. C |
9.. D |
1.0. B |
|
1.1. B |
1.2. B |
|
|
|
PHẦN 2. TỰ LUẬN (7đ)
Bài 1 . (1,5đ)
a) Parabol \(\left( P \right):\,\,y = {x^2} + 2x – 3\) nhận \(x = – 1\) làm trục đối xứng và có đỉnh \(I\left( { – 1; – 4} \right)\)
Một số điểm trên (P):
|
\(x\) |
-3 |
-2 |
-1 |
0 |
1 |
|
\(y\) |
0 |
-3 |
-4 |
-3 |
0 |
Đồ thị hàm số (hình bên):
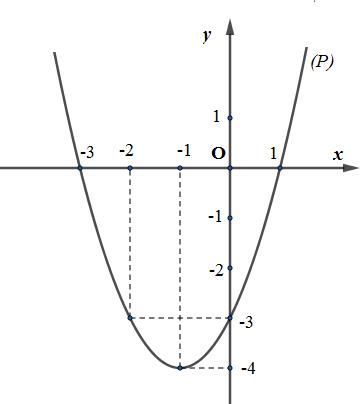
b) Hàm số\(y = {x^2} + 2x – 3\) có \(1 > 0\), đồng biến trên khoảng \(\left( { – 1; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { – \infty ; – 1} \right)\).
Bảng biến thiên của hàm số \(y = {x^2} + 2x – 3\)
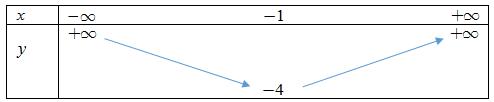
Bài 2 . (2đ)
a) \(\begin{array}{l}\sqrt {2x + 9} = x – 3\\ \Leftrightarrow \left\{ \begin{array}{l}x – 3 \ge 0\\2x + 9 = {\left( {x – 3} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\2x + 9 = {x^2} – 6x + 9\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\{x^2} – 8x = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\\left[ \begin{array}{l}x = 0\\x = 8\end{array} \right.\end{array} \right.\,\,\,\, \Leftrightarrow x = 8\end{array}\)
Vậy, phương trình đã cho có nghiệm \(x = 8\).
b) Gọi số tiền loại \(2000,\,\,5000,\,\,10\,000\) lần lượt là \(x,\,\,y,\,\,z\)
Theo đề bài ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}x + y + z = 1\,200\,000\\x + y = z\\x – y = 200\,000\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}(x + y) + z = 1\,200\,000\\(x + y) – z = 0\\x – y = 200\,000\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x + y = 600\,000\\z = 600\,000\\x – y = 200\,000\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{600\,000 + 200\,000}}{2}\\y = x – 200\,000\\z = 600\,000\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 400\,000\\y = 200\,000\\z = 600\,000\end{array} \right.\end{array}\)
Vậy, số tiền loại \(2000,\,\,5000,\,\,10\,000\) lần lượt là \(400\,000,\,\,200\,000,\,\,600\,000\).
Bài 3 . (3đ)
a) *) Tính \(BC,\,BD\):
Ta có: \(B{C^2} = A{B^2} + A{C^2} – 2.AB.AC.\cos \widehat {BAC}\)
\(\begin{array}{l} = {\left( {2a} \right)^2} + {\left( {3a} \right)^2} – 2.2a.3a.\cos {60^0} \\= {\left( {2a} \right)^2} + {\left( {3a} \right)^2} – 2.2a.3a.\dfrac{1}{2}\\ = 4{a^2} + 9{a^2} – 6{a^2} = 7{a^2}\,\, \Rightarrow BC = a\sqrt 7 \end{array}\)
Do tam giác \(ACD\)dựng vêc phía ngoài tam giác\(ABC\)nên:
\(\widehat {BAD} = \widehat {BAC} + \widehat {CAD} = {60^0} + {90^0} = {150^0}\)
Khi đó:
\(\begin{array}{l}B{D^2} = A{B^2} + A{D^2} – 2.AB.AD.\cos \widehat {BAD}\\ = {\left( {2a} \right)^2} + {\left( {3a} \right)^2} – 2.2a.3a.\cos {150^0}\\ = {\left( {2a} \right)^2} + {\left( {3a} \right)^2} – 2.2a.3a.\dfrac{{ – \sqrt 3 }}{2}\end{array}\)
\(\begin{array}{l} = 4{a^2} + 9{a^2} + 6\sqrt 3 {a^2}\\ = \left( {13 + 6\sqrt 3 } \right){a^2}\,\\\,\, \Rightarrow BD = a\sqrt {13 + 6\sqrt 3 } \end{array}\)
*) Tính \(\overrightarrow {AB} .\,\overrightarrow {AC} ,\,\,\overrightarrow {BD} .\,\overrightarrow {AC} \):
\(\begin{array}{l}\overrightarrow {AB} .\,\overrightarrow {AC} = AB.AC.\cos \left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2a.3a.\cos {60^0} = 3{a^2}\end{array}\)
\(\begin{array}{l}\overrightarrow {BD} .\,\overrightarrow {AC} = \left( {\overrightarrow {BA} + \overrightarrow {AD} } \right).\,\overrightarrow {AC} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \overrightarrow {BA} \,.\overrightarrow {AC} + \,\overrightarrow {AD} .\,\overrightarrow {AC} = \overrightarrow {BA} \,.\overrightarrow {AC} + 0\end{array}\)(do \(AD \bot AC\))
\( = \overrightarrow {BA} \,.\overrightarrow {AC} = – \overrightarrow {AB} \,.\overrightarrow {AC} = – 3{a^2}\)
Vậy, \(BC = a\sqrt 7 \), \(BD = a\sqrt {13 + 6\sqrt 3 } \), \(\overrightarrow {AB} .\,\overrightarrow {AC} = 3{a^2}\), \(\overrightarrow {BD} .\,\overrightarrow {AC} = – 3{a^2}\).
b) Do \(H\) là trực tâm của tam giác \(ABC\) nên \(\left\{ \begin{array}{l}\overrightarrow {AH} .\overrightarrow {BC} = 0\\\overrightarrow {BH} .\overrightarrow {AC} = 0\end{array} \right.\) (*)
Giả sử \(H\left( {a;b} \right)\), khi đó: \(\overrightarrow {AH} = \left( {a – 1;b – 2} \right),\,\,\overrightarrow {BH} = \left( {a + 1;b + 1} \right)\)
Ta có: \(\overrightarrow {BC} = \left( {3;0} \right),\,\,\overrightarrow {AC} = \left( {1; – 3} \right)\)
\(\begin{array}{l}\left( * \right) \Leftrightarrow \left\{ \begin{array}{l}\left( {a – 1} \right).3 + \left( {b – 2} \right).0 = 0\\\left( {a + 1} \right).1 + \left( {b + 1} \right).\left( { – 3} \right) = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a – 1 = 0\\a + 1 – 3b – 3 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = 1\\ – 3b – 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = – \dfrac{1}{3}\end{array} \right.\end{array}\)
Vậy, \(H\left( {1; – \dfrac{1}{3}} \right)\).
Bài 4 . (0,5đ)
ĐKXĐ: \(x \ge \dfrac{1}{2}\)
Phương trình
\(\begin{array}{l}\sqrt {x – \sqrt {2x – 1} } + \sqrt {x + 4 – 3\sqrt {2x – 1} } = \sqrt 2 \\ \Leftrightarrow \sqrt {2x – 2\sqrt {2x – 1} } + \sqrt {2x + 8 – 6\sqrt {2x – 1} } = 2\end{array}\)
\(\begin{array}{l} \Leftrightarrow \sqrt {2x – 1 – 2\sqrt {2x – 1} + 1} + \sqrt {2x – 1 – 6\sqrt {2x – 1} + 9} = 2\\ \Leftrightarrow \sqrt {{{\left( {\sqrt {2x – 1} – 1} \right)}^2}} + \sqrt {{{\left( {\sqrt {2x – 1} – 3} \right)}^2}} = 2\end{array}\)
\( \Leftrightarrow \left| {\sqrt {2x – 1} – 1} \right| + \left| {\sqrt {2x – 1} – 3} \right| = 2\) (*)
Giải phương trình:
\(\begin{array}{l}\sqrt {2x – 1} – 1 = 0\\ \Leftrightarrow \sqrt {2x – 1} = 1\\ \Leftrightarrow 2x – 1 = 1 \Leftrightarrow x = 1\end{array}\)
\(\begin{array}{l}\sqrt {2x – 1} – 3 = 0\\ \Leftrightarrow \sqrt {2x – 1} = 3\\ \Leftrightarrow 2x – 1 = 9 \Leftrightarrow x = 5\end{array}\)
TH1: Nếu \(\dfrac{1}{2} \le x \le 1\) thì
\(\begin{array}{l}\left( * \right) \Leftrightarrow 1 – \sqrt {2x – 1} + 3 – \sqrt {2x – 1} = 2\\ \Leftrightarrow 4 – 2\sqrt {2x – 1} = 2\\ \Leftrightarrow \sqrt {2x – 1} = 1 \Leftrightarrow x = 1\,\,(TM)\end{array}\)
TH2: Nếu \(1 < x < 5\) thì
\(\begin{array}{l}\left( * \right) \Leftrightarrow \sqrt {2x – 1} – 1 + 3 – \sqrt {2x – 1} = 2\\\,\,\,\,\,\,\,\,\, \Leftrightarrow 2 = 2\end{array}\) (luôn đúng)
TH3: Nếu \(x \ge 5\) thì
\(\begin{array}{l}\left( * \right) \Leftrightarrow \sqrt {2x – 1} – 1 + \sqrt {2x – 1} – 3 = 2\\ \Leftrightarrow 2\sqrt {2x – 1} – 4 = 2 \Leftrightarrow \sqrt {2x – 1} = 3\\ \Leftrightarrow x = 5\,\,(TM)\end{array}\)
Vậy, phương trình đã cho có tập nghiệm \(S = \left[ {1;5} \right]\).






