
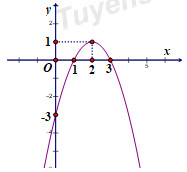
1. : Hàm số nào sau đây có đồ thị như hình bên?
A. \(y = – {x^2} + 2x – 3\).
B. \(y = – {x^2} + 4x – 3\).
C. \(y = {x^2} – 4x + 3\).
D. \(y = {x^2} – 2x – 3\).
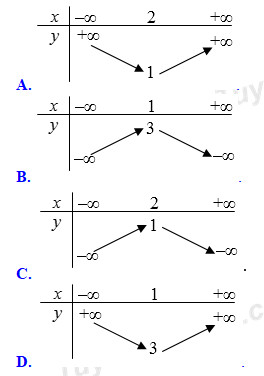
2. : Bảng biến thiên của hàm số \(y = – 2{x^2} + 4x + 1\) là bảng nào sau đây?
3. : Độ dài các cạnh của một đám vườn hình chữ nhật là \(x = 7,8m \pm 2cm\) và \(y = 25,6m \pm 4cm\). Cách viết chuẩn của diện tích (sau khi quy tròn) là:
A. \(200{m^2} \pm 0,9{m^2}\) .
B. \(199{m^2} \pm 0,8{m^2}\).
C. \(199{m^2} \pm 1{m^2}\).
D. \(200{m^2} \pm 1c{m^2}\) .
4. Cho \(\overrightarrow {AB} \) khác \(\overrightarrow 0 \) và cho điểm \(C\). Có bao nhiêu điểm \(D\) thỏa \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\)?
A. Vô số.
B. \(1\) điểm.
C. \(2\) điểm.
D. Không có điểm nào.
5. : Cho giá trị gần đúng của \(\dfrac{8}{{17}}\) là \(0,47\). Sai số tuyệt đối của số \(0,47\) là:
A. \(0,001\). B. \(0,003\).
C. \(0,002\). D. \(0,004\).
6. : Trong mặt phẳng tọa độ `, cho hai điểm ` và `. Điểm \(P\left( {\dfrac{a}{b};0} \right)\) (với \(\dfrac{a}{b}\) là phân số tối giản) trên trục hoành thỏa mãn tổng khoảng cách từ P tới hai điểm A và B là nhỏ nhất. Tính \(S = a + b\).
A. . \(S = – 2\) B. \(S = 8\).
C. \(S = 7\). D. \(S = 4\).
7. : Cho hai tập hợp \(A = \left\{ {x \in R| – 3 < x \le 2} \right\}\), \(B = \left( { – 1;{\rm{ 3}}} \right)\). Chọn khẳng định đúng trong các khẳng định sau :
A. \(A \cap B = \left( { – 1;{\rm{ 2}}} \right]\).
B. \(A\backslash B = \left( { – 3; – 1} \right)\) .
C. \({C_\mathbb{R}}B = \left( { – \infty ; – 1} \right) \cup \left[ {3; + \infty } \right)\).
D. \(A \cup B = \left\{ { – 2; – 1;0;1;2} \right\}\).
8. : Cho \(A = \left\{ {x \in N|x \le 3} \right\}\), \(B = \left\{ {0;1;2;3} \right\}\). Tập \(A \cap B\) bằng:
A. \(\left\{ {1;2;3} \right\}\).
B. \(\left\{ { – 3; – 2; – 1;0;1;2;3} \right\}\).
C. \(\left\{ {0;1;2} \right\}\).
D. \(\left\{ {0;1;2;3} \right\}\).
9. : Cho parabol \(\left( P \right)\)\(y = 3{x^2} – 2x + 1\). Điểm nào sau đây là đỉnh của \(\left( P \right)\)?
A. \(I\left( {0;1} \right)\).
B. \(I\left( {\dfrac{1}{3};\dfrac{2}{3}} \right)\).
C. \(I\left( {\dfrac{{ – 1}}{3};\dfrac{2}{3}} \right)\).
D. \(I\left( {\dfrac{1}{3};\dfrac{{ – 2}}{3}} \right)\).
1.0 : Nghiệm của hệ phương trình \(\left\{ \begin{array}{l}\dfrac{4}{{x – 2}} + \dfrac{1}{y} = 5\\\dfrac{5}{{x – 2}} – \dfrac{2}{y} = 3\end{array} \right.\)là:
A. \(\left( {x;y} \right) = \left( {3;11} \right)\).
B. \(\left( {x;y} \right) = \left( { – 3;1} \right)\).
C. \(\left( {x;y} \right) = \left( {13;1} \right)\).
D. \(\left( {x;y} \right) = \left( {3;1} \right)\).
1.1 : Hai vectơ có cùng độ dài và ngược hướng gọi là:
A. Hai vectơ cùng hướng.
B. Hai vectơ cùng phương.
C. Hai vectơ đối nhau.
D. Hai vectơ bằng nhau.
1.2 : Cho phương trình: \(\dfrac{{{x^2} – 3x – 2}}{{x – 3}} = – x\) có nghiệm \(a\). Khi đó \(a\) thuộc tập:
A. \(\left( {\dfrac{1}{3};3} \right).\)
B. \(\left( { – \dfrac{1}{2};\dfrac{1}{2}} \right).\)
C. \(\left( {\dfrac{1}{3};1} \right).\)
D. \(\emptyset .\)
1.3 : Cho \(A = \left\{ {1;2;3} \right\}\), số tập con của \(A\) là:
A. \(3\). B. \(5\).
C. \(8\). D. 6
1.4 : Trong mặt phẳng tọa độ \(Oxy\), cho tam giác \(ABC\) có trọng tâm là gốc tọa độ \(O,\) hai đỉnh \(A\left( {–2;2} \right)\) và \(B\left( {3;5} \right).\) Tọa độ đỉnh \(C\) là:
A. \(\left( { – 1; – 7} \right)\).
B. \(\left( {2; – 2} \right)\).
C. \(\left( { – 3; – 5} \right)\).
D. \(\left( {1;{\rm{ }}7} \right)\).
1.5 : Cho hai tập hợp \(A = \left[ {1;3} \right]\) và \(B = \left[ {m;m + 1} \right]\). Tìm tất cả giá trị của tham số \(m\) để \(B \subset A\).
A. \(m = 1\).
B. \(1 < m < 2\).
C. \(1 \le m \le 2\)
D. \(m = 2\).
16 : Tập xác định của hàm số \(y = \sqrt {8 – 2x} – x\) là
A. \(\left( { – \infty ;4} \right]\).
B. \(\left[ {4; + \infty } \right)\).
Advertisements (Quảng cáo)
C. \(\left[ {0;4} \right]\).
D. \(\left[ {0; + \infty } \right)\).
17 : Đường thẳng \(d:y = \left( {m – 3} \right)x – 2m + 1\)cắt hai trục tọa độ tại hai điểm \(A\)và \(B\)sao cho tam giác \(OAB\) cân. Khi đó, số giá trị của m thỏa mãn là:
A. 1. B. 0.
C. 3. D. 2.
18 : Cho hàm số \(f(x) = \left\{ \begin{array}{l}\dfrac{{2x + 3}}{{x + 1}}\,\,\,\,khi\,x\, \ge \,0\\\dfrac{{\sqrt[3]{{2 + 3x}}}}{{x – 2}}\,\,khi\, – 2\, \le \,x\, < \,0\end{array} \right.\). Ta có kết quả nào sau đây đúng?
A. \(f\left( { – 1} \right) = \dfrac{1}{3};f\left( 2 \right) = \dfrac{7}{3}\) .
B. \(f\left( 0 \right) = 2;f\left( { – 3} \right) = \sqrt 7 \) .
C. \(f\left( { – 1} \right)\) : không xác định; \(f\left( { – 3} \right) = – \dfrac{{11}}{{24}}\) .
D. \(f\left( { – 1} \right) = \sqrt 8 ;f\left( 3 \right) = 0\) .
19 : Trong các tập hợp sau, tập nào là tập rỗng?
A. \(\left\{ {x \in R\left| {{x^2} + 5x – 6 = 0} \right.} \right\}\).
B. \(\left\{ {x \in Q\left| {3{x^2} – 5x + 2 = 0} \right.} \right\}\).
C. \(\left\{ {x \in Z\left| {{x^2} + x – 1 = 0} \right.} \right\}\).
D. \(\left\{ {x \in R\left| {{x^2} + 5x – 1 = 0} \right.} \right\}\).
2.0 : Trong các phương trình sau, phương trình nào tương đương với phương trình \({\kern 1pt} x – 1 = 0\)?
A. \({\kern 1pt} x + 2 = 0\).
B. \({\kern 1pt} x + 1 = 0\) .
C. \({\kern 1pt} 2x – 2 = 0\) .
D. \({\kern 1pt} (x – 1)(x + 2) = 0\) .
2.1 : Cho hai lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ;\overrightarrow {{F_2}} = \overrightarrow {MB} \) cùng tác động vào một vật tại điểm \(M\) cường độ hai lực \(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} \) lần lượt là \(300N\) và \(400N\). \(\widehat {AMB} = {90^0}\). Tìm cường độ của lực tổng hợp tác động vào vật.
A. \(0N\). B. \(700N\).
C. \(100N\). D. \(500N\).
2.2 : Cho phương trình \(f\left( x \right) = 0\) có tập nghiệm \({S_1} = \left\{ {m;2m – 1} \right\}\) và phương trình \(g\left( x \right) = 0\)có tập nghiệm \({S_2} = \left[ {1;2} \right]\) . Tìm tất cả các giá trị \(m\) để phương trình \(g\left( x \right) = 0\) là phương trình hệ quả của phương trình \(f\left( x \right) = 0\).
A. \(1 < m < \dfrac{3}{2}\)
B. \(1 \le m \le 2\)
C. \(m \in \emptyset .\)
D. \(1 \le m \le \dfrac{3}{2}\)
2.3 : Cho hình bình hành \(ABCD\). Đẳng thức nào sau đây sai.
A. \(\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {BD} } \right|\).
B. \(\left| {\overrightarrow {BC} } \right| = \left| {\overrightarrow {DA} } \right|\).
C. \(\left| {\overrightarrow {AD} } \right| = \left| {\overrightarrow {BC} } \right|\).
D. \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\).
2.4 : Phủ định của mệnh đề ”\(\exists x \in Q:2{x^2} – 5x + 2 = 0\)” là:
A. “\(\exists x \in Q:2{x^2} – 5x + 2 > 0\)”.
B. “\(\exists x \in Q:2{x^2} – 5x + 2 \ne 0\)”.
C. “\(\forall x \in Q:2{x^2} – 5x + 2 \ne 0\)”.
D. “\(\forall x \in Q:2{x^2} – 5x + 2 = 0\)”.
2.5 : Hãy chỉ ra phương trình bậc nhất trong các phương trình sau:
A. \(\dfrac{1}{x} + x = 2\).
B. \( – {x^2} + 4 = 0\).
C. \(\sqrt 2 x – 7 = 0\).
D. \(x.(x + 5) = 0\).
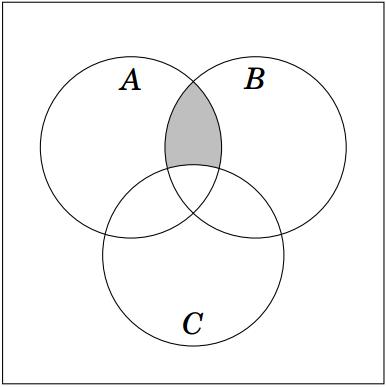
2.6 : Cho các tập hợp \(A,\,B,\,C\) được minh họa bằng biểu đồ Ven như hình bên. Phần tô màu xám trong hình là biểu diễn của tập hợp nào sau đây?
A. \(A \cap B \cap C\).
B. \(\left( {A\backslash C} \right) \cup \left( {A\backslash B} \right)\).
Advertisements (Quảng cáo)
C. \(\left( {A \cup B} \right)\backslash C\).
D. \(\left( {A \cap B} \right)\backslash C\).
2.7 : Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{ – {x^3} – 6}&{;x \le – 2}\\{\left| x \right|}&{; – 2 < x < 2}\\{{x^3} – 6}&{;x \ge 2}\end{array}} \right.\). Khẳng định nào sau đây đúng?
A. Đồ thị của hàm số \(f\left( x \right)\) đối xứng qua gốc tọa độ.
C. \(f\left( x \right)\) là hàm số lẻ.
B. Đồ thị của hàm số \(f\left( x \right)\) đối xứng qua trục hoành.
D. \(f\left( x \right)\) là hàm số chẵn.
2.8 : Số các nghiệm nguyên của phương trình \(x(x + 5) = 2\sqrt[3]{{{x^2} + 5x – 2}} – 2\) là:
A. 0 B. 1
C. 2 D. 3
2.9 : Cho số a= 367 653 964 \( \pm \)213. Số quy tròn của số gần đúng 367 653 964 là:
A. 367 653 960.
B. 367 653 000.
C. 367 654 000.
D. 367 653 970.
3.0 : Câu nào trong các câu sau không phải là mệnh đề?
A. \(\pi \) có phải là một số vô tỷ không?.
B. 2 + 2 = 5.
C. \(\sqrt 2 \) là một số hữu tỷ.
D. \(\dfrac{4}{2}\)= 2.
3.1 : Một xe hơi khởi hành từ Krông Năng đi đến Nha Trang cách nhau \({\rm{175}}\)km. Khi về xe tăng vận tốc trung bình hơn vận tốc trung bình lúc đi là \(20\)km/giờ. Biết rằng thời gian dùng để đi và về là \(6\)giờ; vận tốc trung bình lúc đi là:
A. \(60\) km/giờ.
B. \(45\) km/giờ.
C. \(55\) km/giờ.
D. \(50\) km/giờ.
32 : Hàm số nào trong bốn phương án liệt kê ở A, B, C, D có đồ thị như hình bên:
A. \(y = – x + 2\).
B. \(y = 2x + 1\).
C. \(y = x + 1\).
D. \(y = – x + 1\).
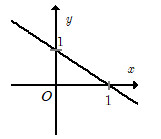
33 : Cho ba điểm \(M,N,P\)thẳng hàng, trong đó điểm \(N\) nằm giữa hai điểm \(M\) và \(P\). Khi đó các cặp vectơ nào sau đây cùng hướng?
A. \(\overrightarrow {MP} \) và \(\overrightarrow {PN} \).
B. \(\overrightarrow {MN} \) và \(\overrightarrow {PN} \).
C. \(\overrightarrow {NM} \) và \(\overrightarrow {NP} \).
D. \(\overrightarrow {MN} \) và \(\overrightarrow {MP} \).
3.4 : Cho tam giác \(ABC\). Điểm \(M\) thỏa mãn \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \). Chọn khẳng định đúng.
A. \(M\) là trọng tâm tam giác .
B. \(M\) là trung điểm của \(BC\).
C. \(M\) trùng với \(B\) hoặc \(C\).
D. \(M\) trùng với \(A\).
3.5 : Cho \(P \Leftrightarrow Q\) là mệnh đề đúng. Khẳng định nào sau đây là sai?
A. \(\bar P \Leftrightarrow Q\) sai.
B. \(\bar P \Leftrightarrow \bar Q\) đúng.
C. \(\bar Q \Leftrightarrow P\) sai.
D. \(\bar P \Leftrightarrow \bar Q\) sai.
3.6 : Tổng \(\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RN} + \overrightarrow {NP} + \overrightarrow {QR} \) bằng:
A. \(\overrightarrow {MR} \).
B. \(\overrightarrow {MN} \).
C. \(\overrightarrow {MP} \).
D. \(\overrightarrow {MQ} \).
37 : Trong mặt phẳng tọa độ \(Oxy,\) cho tam giác \(ABC\) có \(A\left( { – 3;0} \right),{\rm{ }}B\left( {3;0} \right)\) và \(C\left( {2;6} \right).\) Gọi \(H\left( {a;b} \right)\) là tọa độ trực tâm của tam giác đã cho. Tính \(a + 6b.\)
A. \(a + 6b = 5.\)
B. \(a + 6b = 6.\)
C. \(a + 6b = 7.\)
D. \(a + 6b = 8.\)
38 : Cho 4 điểm bất kì \(A,B,C,O\). Đẳng thức nào sau đây đúng?
A. \(\overrightarrow {OA} = \overrightarrow {OB} – \overrightarrow {BA} \).
B. \(\overrightarrow {OA} = \overrightarrow {CA} – \overrightarrow {CO} \).
C. \(\overrightarrow {AB} = \overrightarrow {AC} + \overrightarrow {BC} \).
D. \(\overrightarrow {AB} = \overrightarrow {OB} + \overrightarrow {OA} \).
39 : Cho tam giác \(ABC,{\rm{ }}M\) và \(N\) là hai điểm thỏa mãn: \(\overrightarrow {BM} = \overrightarrow {BC} – 2\overrightarrow {AB} ;\)\(\,\,\,\overrightarrow {CN} = x\overrightarrow {AC} – \overrightarrow {BC} .\) Xác định \(x\) để \(A,{\rm{ }}M,{\rm{ }}N\) thẳng hàng.
A. \(3.\) B. \( – \dfrac{1}{3}.\)
C. \(2.\) D. \( – \dfrac{1}{2}.\)
4.0 : Cho tam giác \(ABC\) có \(I,{\rm{ }}D\) lần lượt là trung điểm\(AB,{\rm{ }}CI\). Đẳng thức nào sau đây đúng?
A. \(\overrightarrow {BD} = \dfrac{1}{2}\overrightarrow {AB} – \dfrac{3}{4}\overrightarrow {AC} \).
B. \(\overrightarrow {BD} = – \dfrac{3}{4}\overrightarrow {AB} + \dfrac{1}{2}\overrightarrow {AC} \).
C. \(\overrightarrow {BD} = – \dfrac{1}{4}\overrightarrow {AB} + \dfrac{3}{2}\overrightarrow {AC} \).
D. \(\overrightarrow {BD} = – \dfrac{3}{4}\overrightarrow {AB} – \dfrac{1}{2}\overrightarrow {AC} \).
4.1 : Kết quả của phép toán \(\left( { – \infty ;\,1} \right) \cap \left[ { – 1;\,2} \right)\) là:
A. \(\left( {1;\,2} \right)\). B. \(\left( { – \infty ;\,2} \right)\).
C. \(\left[ { – 1;\,1} \right)\). D. \(\left( { – 1;\,1} \right)\).
4.2 : Trong mặt phẳng tọa độ \(Oxy\), cho hai điểm \(A\left( {1;0} \right)\) và \(B\left( {0; – 2} \right)\). Tọa độ trung điểm của đoạn thẳng \(AB\) là:
A. \(\left( {\dfrac{1}{2}; – 1} \right)\)
B. \(\left( { – 1;\dfrac{1}{2}} \right)\).
C. \(\left( {\dfrac{1}{2}; – 2} \right)\).
D. \(\left( {1; – 1} \right)\).
4.3 : Tìm \(m\) để phương trình \(m{x^2}–2\left( {m + 1} \right)x + m + 1 = 0\) vô nghiệm.
A. \(m < – 1\).
B. \(m \le 1\) hoặc \(m \ge 0\).
C. \(m = 0\)và \(m < – 1\).
D. \(m = 0\)và \(m > – 1\).
4.4 : Cho hai vectơ \(\vec a\) và \(\overrightarrow b \). Đẳng thức nào sau đây sai?
A. \(\vec a.\overrightarrow b = \dfrac{1}{4}\left( {{{\left| {\vec a + \overrightarrow b } \right|}^2} – {{\left| {\vec a – \overrightarrow b } \right|}^2}} \right).\)
B. \(\vec a.\overrightarrow b = \dfrac{1}{2}\left( {{{\left| {\vec a + \overrightarrow b } \right|}^2} – {{\left| {\vec a – \overrightarrow b } \right|}^2}} \right).\)
C. \(\vec a.\overrightarrow b = \dfrac{1}{2}\left( {{{\left| {\vec a + \overrightarrow b } \right|}^2} – {{\left| {\vec a} \right|}^2} – {{\left| {\overrightarrow b } \right|}^2}} \right).\)
D. \(\vec a.\overrightarrow b = \dfrac{1}{2}\left( {{{\left| {\vec a} \right|}^2} + {{\left| {\overrightarrow b } \right|}^2} – {{\left| {\vec a – \overrightarrow b } \right|}^2}} \right).\)
4.5 : Tính giá trị biểu thức \(P = \sin {30^0}\cos {60^0} + \sin {60^0}\cos {30^0}.\)
A. \(P = 1.\) B. \(P = 0.\)
C. \(P = \sqrt 3 .\) D. \(P = – \sqrt 3 .\)
4.6 : Cho tam giác \(ABC\) với \(\widehat A = {60^0}\). Tính tổng \(\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) + \left( {\overrightarrow {BC} ,\overrightarrow {CA} } \right).\)
A. \({120^0}.\) B. \({360^0}.\)
C. \({270^0}.\) D. \({240^0}.\)
4.7 : Cho hình vuông \(ABCD\) cạnh \(a\) . Khi đó \(\overrightarrow {AB} .\overrightarrow {AC} \) bằng:
A. \({a^2}\).
B. \({a^2}\sqrt 2 \).
C. \(\dfrac{{\sqrt 2 }}{2}{a^2}\).
D. \(\dfrac{1}{2}{a^2}\).
4.8 : Một hàm số bậc nhất \(y = f\left( x \right)\) có \(f\left( {–1} \right) = 2\) và \(f\left( 2 \right) = –3\). Hàm số đó là:
A. \(y = –2x + 3\) .
B. \(f\left( x \right) = \dfrac{{ – 5x + 1}}{3}\).
C. \(y = 2x–3\) .
D. \(f\left( x \right) = \dfrac{{ – 5x – 1}}{3}\) .
4.9 : Cho \(m\) là một tham số thực và hai tập hợp \(A = \left[ {1 – 2m;\,m + 3} \right]\), \(B = \left\{ {x \in R|\,x \ge 8 – 5m} \right\}\). Tất cả các giá trị \(m\) để \(A \cap B = \phi \) là:
A. \(m \ge \dfrac{5}{6}\).
B. \(m < – \dfrac{2}{3}\).
C. \(m \le \dfrac{5}{6}\).
D. \( – \dfrac{2}{3} \le m < \dfrac{5}{6}\).
5.0 : Bộ \(\left( {x;y;z} \right) = \left( {2; – 1;1} \right)\) là nghiệm của hệ phương trình nào sau đây?
A. \(\left\{ \begin{array}{l}x + 3y – 2z = – 3\\2x – y + z = 6\\5x – 2y – 3z = 9\end{array} \right..\)
B. \(\left\{ \begin{array}{l}2x – y – z = 1\\2x + 6y – 4z = – 6\\x + 2y = 5\end{array} \right..\)
C. \(\left\{ \begin{array}{l}3x – y – z = 1\\x + y + z = 2\\x – y – z = 0\end{array} \right..\)
D. \(\left\{ \begin{array}{l}x + y + z = – 2\\2x – y + z = 6\\10x – 4y – z = 2\end{array} \right..\)

|
1. B |
2. C |
3. B |
4. A |
5. A |
|
6. B |
7. A |
8. D |
9. B |
10. D |
|
11. C |
12. B |
13. C |
14. A |
15. C |
|
16. A |
17. C |
18. A |
19. C |
20. C |
|
21. D |
22. D |
23. A |
24. C |
25. C |
|
26. D |
27. D |
28. C |
29. C |
30. A |
|
31. D |
32. D |
33. D |
34. B |
35. D |
|
36. B |
37. C |
38. B |
39. D |
40. B |
|
41. C |
42. A |
43. A |
44. A |
45. A |
|
46. D |
47. A |
48. B |
49. D |
50. A |






