PHẦN TRẮC NGHIỆM (5,0 điểm – Thời gian làm bài 45 phút)
1. : Tập hợp nào sau đây có đúng hai tập hợp con?
A. \(\left\{ {x;\emptyset } \right\}\)
B. \(\left\{ x \right\}\)
C. \(\left\{ {x;y;\emptyset } \right\}\)
D. \(\left\{ {x;y} \right\}\)
2. : Cho \(A = \left( { – 1;3} \right);\,\,B = \left[ {0;5} \right]\). Khi đó \(\left( {A \cap B} \right) \cup \left( {A\backslash B} \right)\) là:
A. \(\left( { – 1;3} \right)\)
B. \(\left[ { – 1;3} \right]\)
C. \(\left( { – 1;3} \right)\backslash \left\{ 0 \right\}\)
D. \(\left( { – 1;3} \right]\)
3. : Parabol \(\left( P \right):\,\,y = – 2{x^2} – 6x + 3\) có hoành độ đỉnh là :
A. \(x = – 3\) B. \(x = \dfrac{3}{2}\)
C. \(x = \dfrac{{ – 3}}{2}\) D. \(x = 3\)
4. : Số nghiệm của phương trình \(\dfrac{x}{{2\sqrt {x – 3} }} = \dfrac{1}{{\sqrt {x – 3} }}\) là :
A. 2 B. 0
C. 1 D. 3
5. : Phương trình \(\left| {3x – 1} \right| = 2x – 5\) có bao nhiêu nghiệm ?
A. Vô số B. 1
C. 0 D. 2
6. : Chiều cao của một ngọn đồi là \(\overline h = 347,13m\,\, \pm \,\,0,2m\). Độ chính xác d của phép đo trên là:
A. \(d = 347,33m\)
B. \(d = 0,2m\)
C. \(d = 347,13m\)
D. \(d = 346,93m\)
7. : Trong mặt phẳng tọa độ Oxy cho hai điểm \(A\left( {3; – 5} \right)\), \(B\left( {1;7} \right)\). Trung điểm I của đoạn thẳng AB có tọa độ là:
A. \(I\left( {2; – 1} \right)\) B. \(I\left( { – 2;12} \right)\)
C. \(I\left( {4;2} \right)\) D. \(I\left( {2;1} \right)\)
8. : Theo thống kê, dân số Việt Nam năm 2016 được ghi lại như sau \(\overline s = 94\,444\,200 \pm 3000\) (người). Số quy tròn của số gần đúng là 94 444 200 là:
A. 94 440 000
B. 94 450 000
C. 94 444 000
D. 94 400 000
9. : Hỏi có bao nhiêu giá trị m nguyên trong nửa khoảng \(\left[ { – 10; – 4} \right)\) để đường thẳng \(d:\,\,y = – \left( {m + 1} \right)x + m + 2\) cắt Parabol \(\left( P \right):\,y = {x^2} + x – 2\) tại hai điểm phân biệt nằm về cùng một phía đối với trục tung?
A. 6 B. 5
C. 7 D. 8
1.0 : Cho \(\overrightarrow u = \overrightarrow {DC} + \overrightarrow {AB} + \overrightarrow {BD} \) với 4 điểm A, B, C, D bất kì. Chọn khẳng định đúng?
A. \(\overrightarrow u = 0\)
B. \(\overrightarrow u = 2\overrightarrow {DC} \)
C. \(\overrightarrow u = \overrightarrow {AC} \)
D. \(\overrightarrow u = \overrightarrow {BC} \)
1.1 : Cho các câu sau đây:
(I): “Phan-xi-păng là ngọn núi cao nhất Việt Nam”.
(II): “\({\pi ^2} < 9,86\)”
(III): “Mệt quá!”
(IV): “Chị ơi, mấy giờ rồi?”
Hỏi có bao nhiêu câu là mệnh đề?
A. 1 B. 3
C. 4 D. 2
Advertisements (Quảng cáo)
1.2 : Hàm số nào sau đây là hàm số lẻ?
A. \(g\left( x \right) = \left| x \right|\)
B. \(k\left( x \right) = {x^2} + x\)
C. \(h\left( x \right) = x + \dfrac{1}{x}\)
D. \(f\left( x \right) = \sqrt {{x^2} + 1} – 2\)
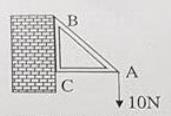
1.3 : Một giá đỡ được gắn vào bức tường như hình vẽ. Tam giác ABC vuông cân ở đỉnh C. Người ta treo vào điểm A một vật có trọng lượng 10N. Khi đó lực tác động vào bức tường tại hai điểm B và C có cường độ lần lượt là :
A. \(10\sqrt 2 N\) và \(10N\)
B. \(10N\) và \(10N\)
C. \(10N\) và \(10\sqrt 2 N\)
D. \(10\sqrt 2 N\)và \(10\sqrt 2 N\)
1.4 : Trong mặt phẳng tọa độ Oxy cho hình bình hành ABCD có \(A\left( { – 2;3} \right);\,\,B\left( {0;4} \right);\,C\left( {5; – 4} \right)\). Tọa độ đỉnh D là :
A. \(\left( {3; – 5} \right)\) B. \(\left( {3;7} \right)\)
C. \(\left( {3;\sqrt 2 } \right)\) D. \(\left( {\sqrt 7 ;2} \right)\)
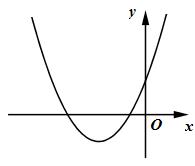
1.5 : Cho hàm số \(y = a{x^2} + bx + c\) có đồ thị như hình vẽ dưới dây. Mệnh đề nào sau đây đúng ?
A. \(a > 0;\,\,b = 0;\,\,c > 0\)
B. \(a > 0;\,\,b > 0;\,\,c > 0\)
C. \(a > 0;\,\,b < 0;\,\,c > 0\)
D. \(a < 0;\,\,b > 0;\,\,c > 0\)
1.6 : Gọi n là số các giá trị của tham số m để phương trình \(\dfrac{{\left( {x + 1} \right)\left( {mx + 2} \right)}}{{x – 2}} = 0\) có nghiệm duy nhất. Khi đó n là :
A. 2 B. 1
C. 0 D. 3
1.7 : Cho hình vuông ABCD cạnh a. Tính \(\left| {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right|\) ?
A. 3a
B. \(\left( {2 + \sqrt 2 } \right)a\)
C. \(a\sqrt 2 \)
D. \(2\sqrt 2 a\)
1.8 : Cho mệnh đề : “Có một học sinh lớp 10A không thích học môn Toán”. Mệnh đề phủ định của mệnh đề này là :
A. “Mọi học sinh lớp 10A đều thích học môn Toán”.
B. “Mọi học sinh lớp 10A đều không thích học môn Toán”.
C. “Mọi học sinh lớp 10A đều thích học môn Văn”.
D. “Có một học sinh lớp 10A thích học môn Toán”.
Advertisements (Quảng cáo)
1.9 : Cho \({0^0} > \alpha < {90^0}\). Khẳng định nào dưới đây đúng ?
A. \(\cot \left( {{{90}^0} + \alpha } \right) = \tan \alpha \)
B. \(\cos \left( {{{90}^0} + \alpha } \right) = – \sin \alpha \)
C. \(\sin \left( {{{90}^0} + \alpha } \right) = – \cos \alpha \)
D. \(\tan \left( {{{90}^0} + \alpha } \right) = \cot \alpha \)
2.0 : Phương trình \(\left( {m + 1} \right){x^2} + \left( {2m – 3} \right)x + m + 2 = 0\) có hai nghiệm phân biệt khi :
A. \(\left\{ \begin{array}{l}m < \dfrac{1}{{24}}\\m \ne – 1\end{array} \right.\)
B. \(\left\{ \begin{array}{l}m \le \dfrac{1}{{24}}\\m \ne – 1\end{array} \right.\)
C. \(m > \dfrac{1}{{24}}\)
D. \(m \le \dfrac{1}{{24}}\)
2.1 : Biết \(\sin \alpha = \dfrac{1}{4}\,\,\left( {{{90}^0} < \alpha < {{180}^0}} \right)\). Hỏi giá trị của \(\cot \alpha \) là bao nhiêu?
A. \( – \dfrac{{\sqrt {15} }}{{15}}\)
B. \( – \sqrt {15} \)
C. \(\sqrt {15} \)
D. \(\dfrac{{\sqrt {15} }}{{15}}\)
2.2 : Trong mặt phẳng tọa độ Oxy, cho \(B\left( {2;3} \right);\,\,C\left( { – 1; – 2} \right)\). Điểm M thỏa mãn \(2\overrightarrow {MB} + 3\overrightarrow {MC} = \overrightarrow 0 \). Tọa độ điểm M là:
A. \(M\left( {\dfrac{1}{5};0} \right)\)
B. \(M\left( { – \dfrac{1}{5};0} \right)\)
C. \(M\left( {0;\dfrac{1}{5}} \right)\)
D. \(\left( {0;\dfrac{{ – 1}}{5}} \right)\)
2.3 : Đường thẳng đi qua điểm \(M\left( {2; – 1} \right)\) và vuông góc với đường thẳng \(y = \dfrac{{ – 1}}{3}x + 5\) có phương trình là:
A. \(y = 3x – 7\)
B. \(y = 3x + 5\)
C. \(y = – 3x – 7\)
D. \(y = – 3x + 5\)
2.4 : Gọi S là tập hợp tất cả các giá trị thực của tham số m để phương trình \(mx + m – \left( {m + 2} \right)x = {m^2} – 2x\) có tập nghiệm là R. Tính tổng tất cả các phần tử của S.
A. 1 B. -1
C. 2 D. 0
2.5 : Hàm số nào sau đây có tập xác định R?
A. \(y = \dfrac{{3x}}{{{x^2} – 4}}\)
B. \(y = {x^2} – 2\sqrt {x – 1} – 3\)
C. \(y = {x^2} – \sqrt {{x^2} + 1} – 3\)
D. \(y = \dfrac{{2\sqrt x }}{{{x^2} + 4}}\)
PHẦN TỰ LUẬN (5,0 điểm – Thời gian làm bài: 45 phút)
1. (2đ) : Cho hàm số \(y = {x^2} – 4x + 3\,\,\,\left( 1 \right)\)
a) (1đ) Lập bảng biến thiên và vẽ đồ thị \(\left( P \right)\) của hàm số (1).
b) (1đ) Viết phương trình đường thẳng đi qua giao điểm của \(\left( P \right)\) với trục Oy và song song với đường thẳng \(y = 12x + 2017\)
2. : Tìm m để phương trình \({x^2} – \left( {2m + 1} \right)x + {m^2} + 1 = 0\) có 2 nghiệm \({x_1};{x_2}\) thỏa mãn \({x_2} = 2{x_1}\).
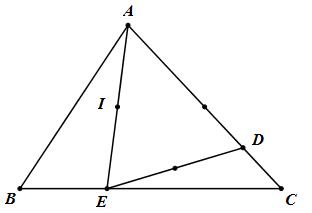
3. (2đ) : Cho tam giác ABC. Trên cạnh AC lấy điểm D, trên cạnh BC lấy điểm E sao cho \(AD = 3DC,\,\,EC = 2BE\).
a) (1đ) Biểu diễn mỗi vectơ \(\overrightarrow {AB} ;\,\,\overrightarrow {ED} \) theo hai vectơ \(\overrightarrow {CA} = \overrightarrow a ;\,\,\overrightarrow {CB} = \overrightarrow b \).
b) (0,5đ) Tìm tập hợp điểm M sao cho \(\left| {\overrightarrow {MA} + \overrightarrow {ME} } \right| = \left| {\overrightarrow {MB} – \overrightarrow {MD} } \right|\).
c) (0,5đ) Với k là số thực tùy ý, lấy các điểm P, Q sao cho \(\overrightarrow {AP} = k\overrightarrow {AD} ;\,\,\overrightarrow {BQ} = k\overrightarrow {BE} .\) Chứng minh rằng trung điểm của đoạn thẳng PQ luôn thuộc một đường thẳng cố định khi k thay đổi.
A. PHẦN TRẮC NGHIỆM
|
1. B |
2. A |
3. C |
4. C |
5. C |
|
6. B |
7. D |
8. A |
9. A |
10. C |
|
11. D |
12. C |
13. A |
14. A |
15. B |
|
16. D |
17. D |
18. A |
19. B |
20. A |
|
21. B |
22. A |
23. A |
24. A |
25. C |
B. PHẦN TỰ LUẬN
1. a) Lập bảng biến thiên và vẽ đồ thị \(\left( P \right)\) của hàm số (1).
TXĐ: \(D = R\)
Tọa độ đỉnh \(I\left( { – \dfrac{b}{{2a}};\dfrac{\Delta }{{4a}}} \right) = \left( {2; – 1} \right)\), trục đối xứng \(x = 2\)
Hàm số đồng biến trên \(\left( { – \infty ;2} \right)\) và nghịch biến trên \(\left( {2; + \infty } \right)\).
Bảng biến thiên:
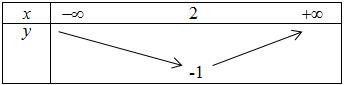*) Đồ thị hàm số:
Giao với trục Ox: Cho \(y = 0 \Rightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right. \Rightarrow \left( {1;0} \right);\,\,\left( {3;0} \right)\)
Giao với trục Oy: Cho \(x = 0 \Rightarrow y = 3\, \Rightarrow \left( {0;3} \right)\).
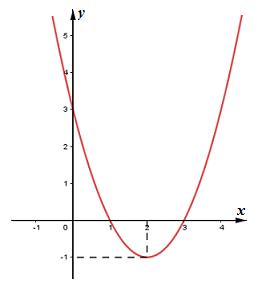
b) \(\left( P \right) \cap Oy = A\left( {0;3} \right)\)
Gọi d là đường thẳng đi qua A và song song với đường thẳng \(y = 12x + 2017\), khi đó phương trình \(\left( d \right)\) có dạng \(y = 12x + c\).
\(A\left( {0;3} \right) \in d \Rightarrow 3 = 0.x + c \Leftrightarrow c = 3\)
\( \Rightarrow \left( d \right):\,\,y = 12x + 3\).
2. Ta có:
\(\begin{array}{l}\Delta = {\left( {2m + 1} \right)^2} – 4\left( {{m^2} + 1} \right)\\\Delta = 4{m^2} + 4m + 1 – 4{m^2} – 4 = 4m – 3\end{array}\)
Để phương trình có 2 nghiệm \({x_1};{x_2} \Leftrightarrow \Delta \ge 0 \) \(\Leftrightarrow 4m – 3 \ge 0 \Leftrightarrow m \ge \dfrac{3}{4}\).
Theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m + 1\\{x_1}{x_2} = {m^2} + 1\end{array} \right.\)
Để 2 nghiệm \({x_1};{x_2}\) thỏa mãn \({x_2} = 2{x_1}\) ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}{x_1} + {x_2} = 2m + 1\\{x_1}{x_2} = {m^2} + 1\\{x_2} = 2{x_1}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}3{x_1} = 2m + 1\\2x_1^2 = {m^2} + 1\\{x_2} = 2{x_1}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_1} = \dfrac{{2m + 1}}{3}\\{x_2} = \dfrac{{2\left( {2m + 1} \right)}}{3}\\2.\dfrac{{{{\left( {2m + 1} \right)}^2}}}{9} = {m^2} + 1\,\,\left( * \right)\end{array} \right.\end{array}\)
Giải (*): \(\begin{array}{l}\dfrac{{2{{\left( {2m + 1} \right)}^2}}}{9} = {m^2} + 1\\ \Leftrightarrow 2\left( {4{m^2} + 4m + 1} \right) = 9\left( {{m^2} + 1} \right)\\ \Leftrightarrow {m^2} – 8m + 7 = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = 7\end{array} \right.\,\,\left( {tm} \right)\end{array}\).
Vậy \(m = 1;\,\,m = 7\).
3.
a) Ta có:
\(\begin{array}{l}\overrightarrow {AB} = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow a + \overrightarrow b \\\overrightarrow {ED} = \overrightarrow {EC} + \overrightarrow {CD} = – \dfrac{2}{3}\overrightarrow {CB} – \dfrac{1}{4}\overrightarrow {AC} = – \dfrac{2}{3}\overrightarrow b – \dfrac{1}{4}\overrightarrow a \end{array}\)
b) Gọi I là trung điểm của AE ta có: \(\overrightarrow {MA} + \overrightarrow {ME} = 2\overrightarrow {MI} \)
\( \Rightarrow \left| {2\overrightarrow {MI} } \right| = \left| {\overrightarrow {DB} } \right|\)
\(\Rightarrow 2MI = BD \Rightarrow MI = \dfrac{{BD}}{2}\)
Do B, D cố định \( \Rightarrow BD\) không đổi \( \Rightarrow \dfrac{{BD}}{2}\) không đổi.
A, E cố định \( \Rightarrow \)I cố định.
Do đó tập hợp điểm M là đường tròn tâm I bán kính \(\dfrac{{BD}}{2}\).
c) Khi \(k = 1 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AP} = \overrightarrow {AD} \Rightarrow P \equiv D\\\overrightarrow {BQ} = \overrightarrow {BE} \Rightarrow Q \equiv E\end{array} \right.\)
\( \Rightarrow PQ \equiv DE \Rightarrow \) Trung điểm của PQ trùng với trung điểm của DE.
Khi \(k = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AP} = \overrightarrow 0 \Rightarrow P \equiv A\\\overrightarrow {BQ} = \overrightarrow 0 \Rightarrow Q \equiv B\end{array} \right.\)
\( \Rightarrow PQ \equiv AB \Rightarrow \) Trung điểm của PQ trùng với trung điểm của AB.
Do AB, DE cố định \( \Rightarrow \) Trung điểm của AB và DE cố định \( \Rightarrow \) Đường thẳng đi qua trung điểm của AB và DE cố định.
Vậy khi k thay đổi thì trung điểm của PQ luôn thuộc đường thẳng cố định đi qua trung điểm của AB và DE.
![[Vật Lý 10 kì 2] Hệ cô lập là gì ? Phát biểu định luật bảo toàn động lượng](https://dethikiemtra.com/wp-content/uploads/2019/04/mon-vat-ly-lop-10-1-100x75.jpg)
