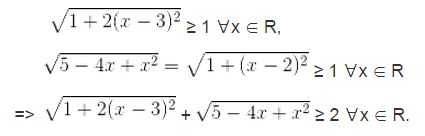Giải bài 1,2,3,4, 5 trang 87,88 SGK Đại số 10: Bất phương trình và hệ bất phương trình một ẩn

Đáp án và Giải bài 1 trang 87; bài 2,3,4,5 trang 88 SGK Đại số 10: Bất phương trình và hệ bất phương trình một ẩn.

Bài 1. Tìm các giá trị x thỏa mãn điều kiện của mỗi BPT sau:

Giải: a) ĐKXĐ: D = {x ∈ R/x ≠ 0 và x + 1 ≠ 0} = R\{0;- 1}.

b) ĐKXĐ: D = {x ∈ R/x² – 4 ≠ 0 và x² – 4x + 3 ≠ 0} = R\{±2; 1; 3}.

c) ĐKXĐ: D = R\{- 1}.

d) ĐKXĐ: D = {x ∈ R/x + 4 ≠ 0 và 1 – x ≥ 0} = (-∞; – 4) ∪ (- 4; 1].

---

Bài 2. Chứng minh các BPT sau vô nghiệm.

a) Gọi D là điều kiện xác định của biểu thức vế trái D = [- 8; +∞]. Vế trái dương với mọi x ∈ D trong khi vế phải là số âm. Mệnh đề sai với mọi x ∈ D. Vậy BPT vô nghiệm.

b)  Vế trái có

Mệnh đề sai ∀x ∈ R. BPT vô nghiệm.

c) ĐKXĐ: D = [- 1; 1]. Vế trái âm với mọi x ∈ D trong khi vế phải dương.

---

Bài 3 trang 88 . Giải thích vì sao các cặp bất phươngtrình sau tương đương?

a) – 4x + 1 > 0 và 4x – 1 <0;

b) 2x² +5 ≤ 2x – 1và 2x² – 2x + 6 ≤ 0;

Giải: a) Tương đương. vì nhân hai vế BPT thứ nhất với -1 và đổi chiều BPT thì được bPT2.

b) Chuyển vế các hạng tử vế phải và đổi dấu ở BPT thứ nhất thì được BPT thứ tương đương.

c) Tương đương. Vì cộng hai vế BPT thứ nhất với  với mọi x ta được BPT3.

d) Điều kiện xác định BPT thứ nhất: D ={x ≥ 1}.

2x + 1 > 0  ∀x ∈ D. Nhân hai vế BPT2. Vậy BPTtương đương.

---

Bài 4. Giải các phương trình sau

a) b) (2x – 1)(x + 3) – 3x + 1 ≤ (x – 1)(x + 3) + x² – 5.
Giải:

a) <=> 

<=> 6(3x + 1) – 4(x – 2) – 3(1 – 2x) < 0

<=> 20x + 11 < 0

<=> 20x < – 11

b) (2x – 1)(x + 3) – 3x + 1 ≤ (x – 1)(x + 3) + x² – 5.

<=> 2x² + 5x – 3 – 3x + 1 ≤ x² + 2x – 3 + x² – 5

<=> 0x ≤ -6.

Vô nghiệm.

---

Bài 5 trang 88 Đại 10. Giải các hệ bất phương trình

Giải: a) 6x + 5/7 < 4x + 7    <=>    6x – 4x < 7 – 5/7
<=>    x < 22/7
8x+3 / 2 < 2x +5  <=>    4x – 2x < 5 – 3/2
<=>    x < 7/4

Tập nghiệm của HBPT:

b) 5x – 2 > 2x + 1/3
<=>      x > 7/39