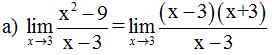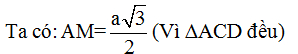Đáp án và Đề thi học kì 1 môn Toán lớp 11 của Sở GD & ĐT Quảng Nam: Chứng minh rằng phương trình x5 + (m – 3)x4 – 2mx3 – 5mx2 + 6mx + 1= 0 luôn có 3 nghiệm phân biệt với mọi giá trị của tham số m.
SỞ GIÁO DỤC VÀ ĐÀO TẠO QUẢNG NAM
Đề Thi Học Kì 1 Môn: Toán – Lớp 11
Thời gian làm bài 90 phút
1. (1,5 điểm). Tính các giới hạn sau:
2 (1,5 điểm). Tìm các giới hạn sau:
3 (1,5 điểm). Tính đạo hàm của các hàm số sau:
a) y = x3 – 5x2 + 1
4. (1,0 điểm).
Xét tính liên tục của hàm số :
tại điểm x = 4.
5. (1,0 điểm). Cho hàm số
Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến này song song với đường thẳng y = –3x –1.
6. (3,0 điểm).
Cho hình chóp S.ABCD, ABCD là hình thoi có cạnh bằng a và góc ABC bằng 60o; SA vuông góc với mặt phẳng (ABCD), SC = 2a.
a. Chứng minh rằng BD vuông góc với mặt phẳng (SAC).
b. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
c. Tính góc giữa hai mặt phẳng (SCD) và (ABCD).
7 (0,5 điểm).
Chứng minh rằng phương trình x5 + (m – 3)x4 – 2mx3 – 5mx2 + 6mx + 1= 0 luôn có 3 nghiệm phân biệt với mọi giá trị của tham số m.
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM ĐỀ THI HK1 TOÁN 11
1. a)
+ Tính đúng giới hạn bằng 1 (0,25 điểm)
b)
= 1 (0,25 đ)
2.
Advertisements (Quảng cáo)
= 6 (0,25 đ)
b)
= -12 ( 0.25 điểm)
3.
a) y’ = (x3)’– (5x2)’+ (1)’
= 3x2 – 10x. (0,5đ)
b)
4.
TXĐ: D = R
f(4) = 3 (0,25 điểm)
Suy ra:
Vậy hàm số f(x) liên tục tại điểm x =4 . (0,25đ)
Advertisements (Quảng cáo)
5.
TXĐ: D = R \ {1}
Gọi (d) là tiếp tuyến của (C) cần tìm.
(d) song song với đường thẳng y =-3x-1
nên (d) có hệ số góc bằng – 3.
+Gọi M(xo;yo) là tiếp điểm của tiếp tuyến (d) với đồ thị (C). Ta có: y’(xo) = -3 (0,25 đ)
Với xo=2, viết được pt (d)
y = -3x + 11 (thỏa) (0,25đ)
Với xo=0, viết được pt (d):
y = -3x – 1 (loại) (0,25đ)
Vậy tiếp tuyến cần tìm là đt y = -3x + 11
6.
a)
CM được BD ⊥ AC (0,25 điểm)
+CM được BD ⊥ SA (0,25 điểm)
+Suy ra : BD ⊥ (SAC) (đpcm) (0,25 điểm)
b)
SA (ABCD) và SC(ABCD) = C
=>AC là hình chiếu vuông góc của SC lên mp(ABCD) (0,25 điểm)
Tính góc :
Trong ∆SAC vuông tại A, ta có:
AC = a (Vì ∆ACD đều), SC =2a =2AC => ∆SAC là nửa tam giác đều cạnh 2a, đường cao SA => =60o. (0,25 điểm)
+ Vậy góc giữa SC và mp(ABCD) bằng 60o. (0,25 điểm)
c)
+(SCD) ∩ (ABCD) = CD
+Kẻ AM ⊥ CD (M là trung điểm của CD vì ∆ACD đều)
+Ta có: SA ⊥ (ABCD) => CD ⊥ SA
Suy ra: CD ⊥ SM (0,25 đ)
=> Góc SMA = β là góc giữa 2 mp (SCD) và (ABCD)
+ Tính góc β : Xét ∆SAM vuông tại A
SA2= SC2 – AC2 = 3a2 (vì ∆SAC vuông tại A) => SA = a√3 (0,25đ)
Suy ra: tan β = = 2 (*) (0,25đ)
(β ≈ 63043’)
7.
TXĐ: D = R
+ Xét hàm số:
f(x) = x5 + (m – 3)x4 – 2mx3 – 5mx2 + 6mx + 1
+ Vì f(x) là hàm đa thức nên liên tục trên R.
+ f(-2) = – 79, f(0) = 1 (0,25đ)
=> f(-2).f(0) < 0 => pt f(x) = 0 có nghiệm x1 (-2 ; 0)
+ f(1) = – 1 => f(0).f(1) < 0
=> pt f(x) = 0 có nghiệm x2 (0 ; 1)
+ f(3) = 1 => f(1).f(3) <0 (0,25đ)
=> pt f(x) = 0 có nghiệm x3 (1 ; 3)
Vậy pt đã cho có 3 nghiệm phân biệt x1, x2, x3 nêu trên với mọi giá trị của tham số m, (đpcm)