Ôn tập chương 2 Toán 9 tập 1: giải bài 32, 33, 34, 35, 36, 37 trang 61; Giải bài 38 SGK trang 62: Ôn tập chương 2 Đại số Toán lớp 9 tập 1: Hàm số bậc nhất.
Bài 32. a) Với những giá trị nào của m thì hàm số bậc nhất y = (m-1)x + 3 đồng biến?
b) Với những giá trị nào của k thì hàm số bậc nhất y = (5 -k)x +1 nghịch biến?
Gợi ý bài 32:
a) Hàm số bậc nhất y = (m – 1)x +3 đồng biến
⇔ m -1 > 0
⇔ m > 1
Vậy: Với m > 1 thì hàm số đồng biến
b)
Hàm số bậc nhất y = (5 – k)x+1 nghịch biến
⇔ 5 – k < 0
⇔ k > 5
Vậy: Với k > 5 thì hàm số nghịch biến
Bài 33. Với những giá trị nào của m thì đồ thị các hàm số y = 2x + (3 +m) và y = 3x + (5-m) cắt nhau tạo một điểm trên trục tung?
Giải: Các hàm số y = 2x + (3 +m) và y = 3x + (5-m) đều là hàm số bật nhất đối với x và hệ số x đều khác 0. Đồ thị của chúng là các đường thẳng cắt trục tung tại một điểm có tung độ là b. Do đó hai đường thẳng cắt nhau tại cùng một điểm trên trục tung, khi và chỉ khi tung độ gốc của chúng bằng nhau, nghĩa là:
3 + m = 5 – m ⇔ m = 1
Vậy khi m =1 thì hai đường thẳng đã cho cắt nhau tại một điểm trên trục tung.
Bài 34. Tìm giá trị của a để hai đường thẳng y = (a-1)x + 2 (a ≠ 1) và y = (3-a)x + 1 (a ≠ 3) song song với nhau.
Giải: Hai đường thẳng y = (a -1)x +2 (a ≠1) và
y =(3 – a)x+1 (a ≠3) song song với nhau
⇔ a – 1 = 3 – a ; a ≠ 1; a ≠ 3( đã có 2 ≠ 1)
⇔ a = 2 (nhận )
Vậy: Với a = 2 thì hai đường thẳng đã cho song song.
Bài 35 trang 61. Xác định k và m để hai đường thẳng sau đây trùng nhau:
y = kx + (m -2) (k ≠ 0); y = (5-k)x + (4-m) (k≠5)
Giải: Hai đường thẳngy = kx + (m -2) (k ≠ 0); y = (5-k)x + (4-m) (k≠5) trùng nhau khi và chỉ khi
k = 5 – k (1)
m – 2 = 4 – m (2)
Từ (1), ta có 2k = 5 ⇔ k =2,5
Từ (2), ta có 2m = 6 ⇔ m = 3
Vậy:điều kiện để hai đường thẳng trùng nhau là: k =2,5 và m=3
Bài 36. Cho hàm số bậc nhất y = (k+1)x +3 và y = (3-2k)x + 1.
a) Với giá trị nào của k thì đồ thị của hai hàm số là hai đường thẳng song song với nhau
b) Với giá trị nào của k thì đồ thị của hàm số là hai đường thẳng cắt nhau?
c) Hai đường thẳng nói trên có thể trùng nhau không? Tại sao?
Advertisements (Quảng cáo)
Lời giải: y = (k+1)x +3 (d)
và y = (3-2k)x + 1 (d’)
Các hàm số đã cho là hàm số bậc nhất khi:

a) Vì đã có 3 ≠ 1 nên (d) // (d’) khi và chỉ khi
k+1 = 3 – 2k
k = 2/3 (TMĐK (*))
Vậy với k = 2/3 thì đồ thị của hai hàm số là hai đường thẳng (d) và (d’) song song với nhau.
b) Hai đường thẳng (d) cắt (d’) khi và chỉ khi k+1 ≠ 3 – 2k
k ≠ 2/3
Vậy với k ≠ -1, k ≠3/2 và k ≠ 2/3 thì đồ thị của hai hàm số là hai đường thẳng (d) và (d’) cắt nhau.
c) Hai đường thẳng (d) và (d’) không thể trùng nhau vì có tung độ gốc khác nhau (do 3 ≠ 1).
Bài 37 (Ôn tập chương 2 Toán Đại số 9) a) Vẽ đồ thị hai hàm số sau trên cùng một mặt phẳng tọa độ: y = 0,5x + 2 (d) và y = 5 – 2x (d’)
b) Gọi giao điểm của các đường thẳng (d) và (d’) với trục hoành Ox theo thứ tự là A, B và giao điểm của hai đường thẳng là C. Tìm tọa độ các điểm A, B, C?
c) Tính độ dài các đoạn thẳng AB, AC và BC biết đơn vị đo trên trục tọa độ là centimet (làm tròn đến chữ số thập phân thứ hai)
d) Tính các góc tạo bởi các đường thẳng (d) và (d’) với trục hoành Ox (làm tròn đến phút).
Gợi ý bài 37: a) Vẽ đồ thị
a) Vẽ đồ thị
- Vẽ đồ thị: y = 0,5x + 2
Cho x = 0 => y =2 vậy: (0;2);
Advertisements (Quảng cáo)
Cho y = 0 => x= -4 vậy: (-4; 0)
- vẽ đồ thị y = 5 – 2x
Cho x = 0 => y = 5 vậy: (0;5)
Cho y = 0 => x = 2,5 vậy: (2,5; 0)
b) Tọa độ của hai điểm A (- 4; 0) và B (2,5 ; 0)
Vì C là giao điểm của hai đường thẳng nên ta có pt hoành độ giao điểm:
0,5x + 2 = 5 – 2x ⇔ x = 1,2
Thay x = 1,2 vào y = 0,5x + 2 ta được:
y = 0,5. 1,2 + 2 = 2,6
Vậy C (1,2 ; 2,6)
c) AB = OA + OB = 4 + 2,5 = 6,5 cm
Gọi F là hình chiếu của C trên Ox, ta có:
OF = 1,2 cm ; FB = 1,3 cm và AF = 5,2 cm
Áp dụng định lý Pitago vào các tam giác vuông ACF và BCF ta có:
AC = √(AF2 + CF2) = 5,22 + 2,62 ≈ 5,81 cm
BC = √(CF2 + BF2) = 2,62 + 1,32 ≈ 2,91 cm
d) Gọi α là góc tạo bởi đường thẳng y = 0,5x + 2 và trục Ox, ta có:
tgα = OD/OA = 2/4 = 0,5 ⇔ α ≈ 26o34’
Gọi β là góc tạo bởi đường thẳng y = 5 – 2x và trục Ox và β’ là góc kề bù với β, ta có:
tgβ’ = OE /OB = 5/2,5 = 2 ⇔ β’ ≈ 63o26’ ⇔ β = 180o – 63o26’ = 116o34’.
Bài 38. a) Vẽ đồ thị các hàm số sau trên cùng một mặt phẳng tọa độ:
y = 2x (1); y = 0,5x (2); y = -x + 6 (3)
b) Gọi các giao điểm của đường thẳng có phương trình (3) với hai đường thẳng có phương trình (1) và (2) theo thứ tự là A và B.
Tìm tọa độ của hai điểm A và B.
c) Tính các góc của tam giác OAB.
a) Đồ thị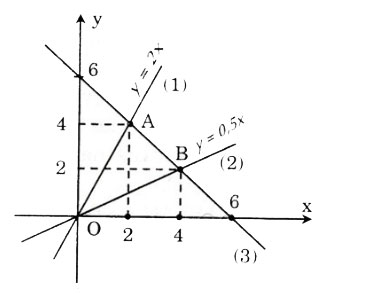
b) Hoành độ điểm A là nghiệm của phương trình: 2x = -x + 6. Từ đó ta tính được: A(2;4).
Hoành độ điểm B là nghiệm của phương trình: 0,5x = -x + 6.
Từ đó ta tính được : B(4;2).
c) Ta có
OA2 = 42 + 22 = 20 ⇒ OA = √20
OB2 = 22 + 42 = 20 ⇒ OB = √20
OA = OB ⇒ ΔAOB cân, đỉnh O.
Ta lại có: tgBOx = 2 ⇒ ∠BOx ≈ 26033′
∠AOx ≈ 63026′
∠AOB = 63026′ – 26033′ = 36053′
∠OAB = ∠OBA = 1/2(1800 – 36053′) =71033′
Bài tập làm thêm:
Bài 1: Tìm giá trị của k sao cho đồ thị hai hàm số bậc nhất :
y = (5k+1)x- 3 và y = (3k-2)x+2 là hai đường thẳng cắt nhau tại điểm có hoành độ bằng -3.
Bài 2: Cho biết đường thẳng y =ax+5 cắt trục hoành tại điểm B có hoành độ bằng -3, đường thẳng y = a’x+ 2,4 cắt trục hoành tại điểm C có hoành độ bằng 4 và hai đường thẳng này cắt nhau tại A.
a/ Tìm a, a’
b/ Vẽ đồ thị hai hàm số với a, a’ tìm được ở câu a/ trên cùng hệ trục tọa độ Oxy
c/ Tìm tọa độ giao điểm A
d/ Tính các góc của tam giác ABC (tính đến đơn vị phút)
e/ Tính chu vi và diện tích của tam giác ABC

![[THCS Bình Giang] kiểm tra môn Sử lớp 9: Em hãy trình bày ngắn gọn diễn biến, kết quả của chiến dịch lịch sử Điện Biên Phủ năm 1954?](https://dethikiemtra.com/wp-content/uploads/2019/03/dongphongnha-100x75.jpg)




