Kiểm tra 45 phút Chương 1 Hình học 12 – Khối đa diện: Trong các mệnh đề sau đây, mệnh đề nào đúng?

1. Cho khối chóp có thể tích \(V\), diện tích đáy là \(S\) và chiều cao \(h\). Chọn công thức đúng:

A. \(V = Sh\)               B. \(V = \dfrac{1}{2}Sh\)

C. \(V = \dfrac{1}{3}Sh\)           D. \(V = \dfrac{1}{6}Sh\)

2. Một khối chóp có đáy là đa giác \(n\)cạnh. Trong các mệnh đề sau đây, mệnh đề nào đúng?

A. Số mặt và số đỉnh bằng nhau

B. Số đỉnh của khối chóp bằng \(n\)

C. Số cạnh của khối chóp bằng \(n + 1\)

D. Số mặt của khối chóp bằng \(2n\)

3. Cho khối chóp tam giác \(S.ABC\), trên các cạnh \(SA,SB,SC\) lần lượt lấy các điểm \(A’,B’,C’\). Khi đó:

 \(A.\,\,\dfrac{{{V_{S.A’B’C’}}}}{{{V_{S.ABC}}}} = \dfrac{{SA’}}{{SA}} + \dfrac{{SB’}}{{SB}} + \dfrac{{SC’}}{{SC}}\)

\(B.\,\,\dfrac{{{V_{S.ABC}}}}{{{V_{S.A’B’C’}}}} = \dfrac{{SA’}}{{SA}}.\dfrac{{SB’}}{{SB}}.\dfrac{{SC’}}{{SC}}\)

\(C.\,\,\,\dfrac{{{V_{S.A’B’C’}}}}{{{V_{S.ABC}}}} = \dfrac{{SA’}}{{SA}} = \dfrac{{SB’}}{{SB}} = \dfrac{{SC’}}{{SC}}\)

\(D.\dfrac{{{V_{S.A’B’C’}}}}{{{V_{S.ABC}}}} = \dfrac{{SA’}}{{SA}}.\dfrac{{SB’}}{{SB}}.\dfrac{{SC’}}{{SC}}\)

4. Đáy của hình chóp \(S.ABCD\) là một hình vuông cạnh \(a\). Cạnh bên \(SA\) vuông góc với mặt đáy và có độ dài là \(a\). Thể tích khối tứ diện \(S.BCD\) bằng:

 \(A.\,\,\dfrac{{{a^3}}}{6}\)             \(B.\,\,\dfrac{{{a^3}}}{3}\)

\(C.\,\,\dfrac{{{a^3}}}{4}\)              \(D.\,\,\dfrac{{{a^3}}}{8}\)

5. Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất:

A. Năm mặt                B. Hai mặt

C. Ba mặt                    D. Bốn mặt

6. Hình tứ diện đều có mấy mặt phẳng đối xứng?

A. \(6\)                         B. \(5\)

C. \(4\)                         D. \(3\)

7. Trong các mệnh đề sau, mệnh đề nào sai?

A. Hình tạo bởi hai tứ diện đều ghép với nhau là một đa diện lồi.

B. Tứ diện đều là đa diện lồi.

C. Hình lập phương là đa diện lồi

D. Hình bát diện đều là đa diện lồi.

8. Khối mười hai mặt đều là khối đa diện đều loại:

A.\(\left\{ {3;5} \right\}\)                    B.\(\left\{ {3;6} \right\}\)

C.\(\left\{ {5;3} \right\}\)                    C. \(\left\{ {4;4} \right\}\)

9. Một hình trụ có bán kính đáy a, có thiết diện qua trục là một hình vuông. Tính diện tích xung quanh của hình trụ.

\(A.\,\,3\pi {a^2}\)                       \(B.\,\,4\pi {a^2}\)

\(C.\,\,2\pi {a^2}\)                       \(D.\,\,\pi {a^2}\)

10: Phép vị tự tỉ số \(k > 0\) biến khối chóp có thể tích \(V\) thành khối chóp có thể tích \(V’\). Khi đó:

\(A.\,\,\dfrac{V}{{V’}} = k\)             \(B.\,\,\dfrac{{V’}}{V} = {k^2}\)

\(C.\,\,\dfrac{V}{{V’}} = {k^3}\)           \(D.\,\,\dfrac{{V’}}{V} = {k^3}\)

11: Hãy chọn cụm từ (hoặc từ) cho dưới đây để sau khi điền nó vào chỗ trống mệnh đề sau trở thành mệnh đề đúng:

“Số cạnh của một hình đa diện luôn……………….số đỉnh của hình đa diện ấy”

A. nhỏ hơn         B. nhỏ hơn hoặc bằng

C. lớn hơn          D. bằng

12: Hình nào sau đây có mặt phẳng đối xứng?

A. hình tứ diện

B. hình chóp có đáy là hình vuông

C. hình chóp tam giác đều

D. hình chóp có đáy là hình chữ nhật

13: Một hình hộp đứng có đáy là hình thoi (không phải là hình vuông) có bao nhiêu mặt phẳng đối xứng:

A. 3 mặt phẳng

B. 2 mặt phẳng

C. 1 mặt phẳng

D. 4 mặt phẳng

14: Trung điểm các cạnh của một tứ diện đều là:

A. Các đỉnh của một hình tứ diện đều

B. Các đỉnh của một hình bát diện đều

C. Các đỉnh của một hình mười hai mặt đều

D. Các đỉnh của một hình hai mươi mặt đều

15. Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình vuông tại \(A\) và \(D\) thỏa mãn \(SA \bot \left( {ABCD} \right)\) và \(AB = 2AD = 2CD = 2a = \sqrt 2 SA\). Thể tích khối chóp \(S.BCD\) là:

\(A.\,\,\,\dfrac{{2{a^3}\sqrt 2 }}{3}\)        \(B.\,\,\dfrac{{{a^3}\sqrt 2 }}{6}\)

\(C.\,\,\dfrac{{2{a^3}}}{3}\)              \(D.\,\,\,\dfrac{{{a^3}\sqrt 2 }}{{12}}\)

16: Cho lăng trụ tam giác ABC. A’B’C’ có thể tích là V, khi đó thể tích của khối chóp A’. ABC là:

\(A.\,\,\dfrac{V}{3}\)                  \(B.\,\,\dfrac{V}{4}\)

\(C.\,\,\dfrac{V}{6}\)                   \(D.\,\,\dfrac{V}{2}\)

17: Số mặt phẳng đối xứng của mặt cầu là:

A. \(6\)             B. \(3\)

C. \(0\)             D. Vô số

18: Có tất cả bao nhiêu khối đa diện đều?

A.\(5\)                     B.\(4\)

C. Vô số             D. \(3\)

19: Chọn khẳng định đúng trong các khẳng định sau:

A. Hình bát diện đều có 8 đỉnh

B. Hình bát diện đều có các mặt là bát giác đều

C. Hình bát diện dều có các mặt là hình vuông

D. Hình bát diện đều là đa diện đều loại {3;4}

20: Cho khối hộp ABCD. A’B’C’D’. Gọi O là giaocủa AC và BD. Tính tỷ số thể tích của khối chóp O. A’B’C’D’ và khối chóp đã cho.

\(A.\,\,\dfrac{1}{3}\)                   \(B.\,\,\dfrac{1}{6}\)

\(C.\,\,\dfrac{1}{2}\)                  \(D.\,\,\dfrac{1}{4}\)

1. Chọn C.

2. Khối chóp có đáy là đa giác \(n\)cạnh thì có \(n + 1\)đỉnh (gồm đỉnh \(S\)và \(n\)đỉnh của đa giác đáy),

\(n + 1\)mặt (\(1\)mặt đáy và \(n\)mặt bên) và \(2n\) cạnh (\(n\)cạnh bên và \(n\)cạnh đáy)

Do đó chỉ có ý A đúng.

Chọn A

3. Nếu \(A’,B’,C’\) là ba điểm lần lượt nằm trên các cạnh \(SA,SB,SC\) của hình chóp tam giác \(S.ABC\). Khi đó:

\(\dfrac{{{V_{S.A’B’C’}}}}{{{V_{S.ABC}}}} = \dfrac{{SA’}}{{SA}}.\dfrac{{SB’}}{{SB}}.\dfrac{{SC’}}{{SC}}\)

Chọn D.

4.

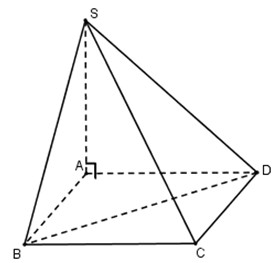
Ta có: \({S_{\Delta BCD}} = \dfrac{1}{2}{S_{ABCD}} = \dfrac{1}{2}{a^2}\)

\({V_{S.BCD}} = \dfrac{1}{3}SA.{S_{BCD}} = \dfrac{1}{3}a.\dfrac{1}{2}{a^2} = \dfrac{{{a^3}}}{6}\)

Chọn A.

5. Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất 3 mặt (ví dụ các đỉnh của hình tứ diện)

Không tồn tại 1 đỉnh nào đó của đa diện nào đó là đỉnh chung của ít hơn 3 mặt

Chọn C.

6. Tứ diện đều có mặt phẳng đối xứng là mặt phẳng đi qua 1 cạnh và trung điểm cạnh đối diện. Vì tứ diện đều có 6 cạnh nên có 6 mặt phẳng đối xứng.

Chọn A.

7. Các hình tứ diện đều, lập phương, bát diện đều là các khối đa diện đều nên chúng là đa diện lồi.

Hình tạo bởi hai tứ diện đều ghép với nhau có thể là đa diện lồi hoặc không phải là đa diện lồi

⇒ Mệnh đề “Hình tạo bởi hai tứ diện đều ghép với nhau là đa diện lồi” là mệnh đề sai

Chọn A.

8. Khối mười hai mặt đều thuộc loại \(\left\{ {5;3} \right\}\).

Chọn C.

9. Chọn B

10: Phép vị tự tỉ số \(k > 0\) biến khối chóp có thể tích \(V\) thành khối chóp có thể tích \(V’\). Khi đó \(\dfrac{{V’}}{V} = {k^3}\).

Chọn D.

11: Hình tứ diện có 6 cạnh và 4 mặt nên số cạnh của tứ diện lớn hơn số mặt của nó.

Chọn C.

12: Tứ diện đều có mặt phẳng đối xứng là mặt phẳng đi qua 1 cạnh và trung điểm cạnh đối diện. Vì tứ diện đều có 6 cạnh nên có 6 mặt phẳng đối xứng.

Chọn A.

13: Chọn A

14: Chọn B

15:

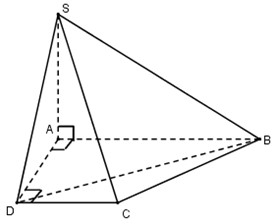
Ta có: \({S_{ABCD}} = \dfrac{1}{2}\left( {AB + CD} \right).AD = \dfrac{1}{2}\left( {2a + a} \right)a = \dfrac{{3{a^2}}}{2}\)

\({S_{\Delta ABD}} = \dfrac{1}{2}AD.AB = \dfrac{1}{2}a.2a = {a^2}\)

\( \Rightarrow {S_{BCD}} = {S_{ABCD}} – {S_{ABD}} = \dfrac{{3{a^2}}}{2} – {a^2} = \dfrac{{{a^2}}}{2}\)

\(SA = \dfrac{{2a}}{{\sqrt 2 }} = a\sqrt 2 \)

\( \Rightarrow {V_{S.BCD}} = \dfrac{1}{3}SA.{S_{BCD}} = \dfrac{1}{3}a\sqrt 2 .\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}\sqrt 2 }}{6}\)

Chọn B.

16: Chọn A

17: Mọi mặt phẳng đi qua tâm của mặt cầu đều là mặt phẳng đối xứng của mặt cầu.

Vậy có vô số mặt phẳng đối xứng.

Chọn D.

18: Có 5 và chỉ 5 khối đa diện đều.

Chọn A.

19: Vì mỗi mặt cảu hình bát diện đều là một tam giác đều và mỗi đỉnh của hình bát diện đều là đỉnh chung của 4 cạnh.

Vậy hình bát diện đều là đa diện đều loại {3;4}

Chọn D.

20:

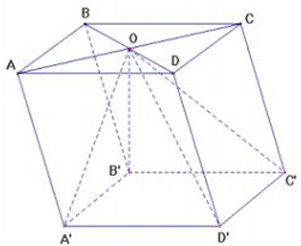
Khối chóp O. A’B’C’ D’ và khối hộp đã cho có cùng đáy là tứ giác A’B’C’D’ và cùng chiều cao là khoảng cách từ O đến mp(A’B’C’ D’) nên:

\(\begin{array}{l}{V_{O.A’B’C’D’}} = \dfrac{1}{3}{V_{ABCD.A’B’C’D’}}\\ \Rightarrow \dfrac{{{V_{O.A’B’C’D’}}}}{{{V_{ABCD.A’B’C’D’}}}} = \dfrac{1}{3}\end{array}\)

Chọn A