
Cho góc nhọn AMB nội tiếp trong đường tròn (O). Trên nửa mặt phẳng bờ AB không chứa M, vẽ tia Ax sao cho \(\widehat {xAB} = \widehat {AMB}\). Chứng tỏ Ax là tiếp tuyến của (O).

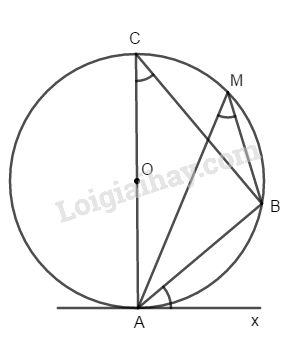
Vẽ đường kính AC của (O), ta phải chứng minh Ax vuông góc AC.
Thật vậy, ta có :
\(\widehat {ACB} = \widehat {AMB}\) (1)
Advertisements (Quảng cáo)
( góc nội tiếp cùng chắn cung AB)
\(\widehat {AMB} = \widehat {xAB}\) (gt) (2)
mà \(\widehat {CBA} = 90^\circ \) ( AC là đường kính)
Advertisements (Quảng cáo)
\(\Rightarrow \widehat {ACB} + \widehat {CAB} = 90^\circ \) (3)
Từ (1), (2) và (3) suy ra \(\widehat {CAB} + \widehat {xAB} = 90^\circ \)
Chứng tỏ Ax là tiếp tuyến của (O.
Xin các bạn lưu ý : Bài toán này là phần đảo của định lí về góc của tiếp tuyến và một dây, dùng để chứng minh.


![[THCS Tô Vĩnh Diện] thi học kì 2 môn Ngữ Văn lớp 9 năm 2020: Trình bày ngắn gọn cảm nhận của em về nhân vật “tôi” trong đoạn trích ở phần: Đọc hiểu văn bản](https://dethikiemtra.com/wp-content/uploads/2020/06/canh-dong-100x75.jpg)
![[THCS & THPT Long Bình] kiểm tra cuối năm học lớp 9 môn Văn: Truyện được trần thuật từ nhân vật nào? Việc chọn vai kể như vậy có tác dụng gì?](https://dethikiemtra.com/wp-content/uploads/2020/09/images-100x75.jpg)

