Bài 1. Cho điểm M nằm bên trong đường tròn (O; R). Dựng qua M hai dây AB và CD sao cho \(AB > CD\). Gọi H, K theo thứ tự là trung điểm của AB và CD. Chứng minh rằng : \(MH > MK.\)
Bài 2. Cho đường tròn (O) đường kính AB. Chứng minh rằng nếu hai dây cung AC và BD song song thì bằng nhau.
Bài 1.
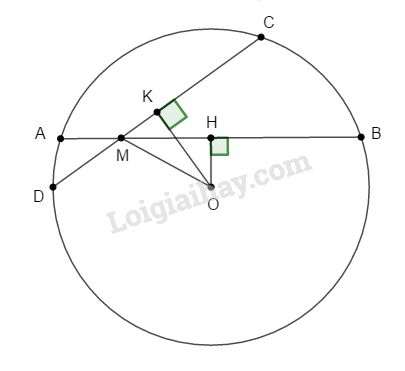
Nối M với O. Xét tam giác vuông OHM, ta có:
\(HM = \sqrt {O{M^2} – O{H^2}}\)\(\; = \sqrt {O{M^2} – O{H^2}} \) (định lí Pi-ta-go)
Advertisements (Quảng cáo)
Tương tự với tam giác vuông OKM, có:
\(KM = \sqrt {O{M^2} – O{K^2}} \)
Mà \(AB > CD ⇒ OH < OK\)
Do đó \(MH > MK\)
Bài 2.
Advertisements (Quảng cáo)
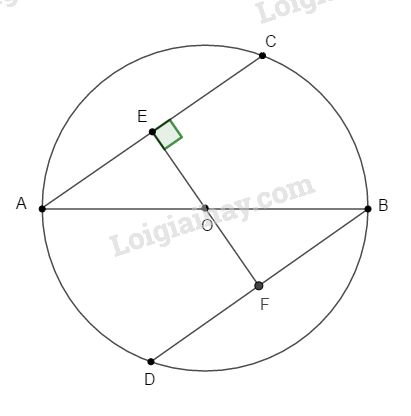
Kẻ \(OE ⊥ AC\) thì đường thẳng \(OE ⊥ BD\) và cắt BD tại F (vì AC // BD)
Xét hai tam giác vuông AEO và BOF có:
+) \(OA = OB (=R)\)
+) \({\widehat O_1} = {\widehat O_2}\) (đối đỉnh)
Do đó \(∆AEO = ∆BOF\) (cạnh huyền – góc nhọn)
\(⇒ OE = OF\)
\(⇒ AC = BD\) (định lí dây cung và khoảng cách đến tâm).
