
Cho \(∆ABC\) cân tại A có \(AB = AC = 50cm, BC = 60cm\). Các đường cao AD và CE cắt nhau tại H. Tính CH.

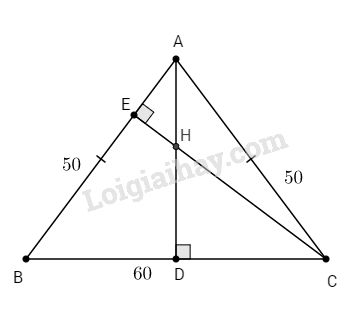
Ta có: \(∆ABC\) cân tại A nên đường cao AD đồng thời là đường trung tuyến:
\(DB = DC = {{BC} \over 2} = {{60} \over 2} = 30\,\left( {cm} \right)\)
Xét \(∆ADB\) có:
Advertisements (Quảng cáo)
\(A{D^2} = A{B^2} – D{B^2}\) (định lí Pi-ta-go)
\( \Rightarrow AD = \sqrt {A{B^2} – D{B^2}} \)\(\;= \sqrt {{{50}^2} – {{30}^2}} = 40\,(cm)\)
Lại có: \( {S_{ABC}} = {1 \over 2}BC.AD = {1 \over 2}AB.CE \)
\(\Rightarrow CE = {{BC.AD} \over {AB}} = {{60.40} \over {50}} = 48\,\left( {cm} \right) \)
Advertisements (Quảng cáo)
Ta có: \(∆CDH\) đồng dạng \(∆CEB\) (g.g)
\( \Rightarrow {{CH} \over {CB}} = {{DC} \over {CE}}\)
\(\Rightarrow CH = {{CB.DC} \over {CE}} = {{60.30} \over {48}} = 37,5\,\left( {cm} \right)\)



![[Phòng GD Bảo Lộc] kiểm tra cuối học kì 2 môn Toán lớp 9: Cạnh huyền của một tam giác vuông bằng 10cm. Tính độ dài các cạnh góc vuông biết chu vi tam giác vuông là 24cm](https://dethikiemtra.com/wp-content/uploads/2020/09/anh-chup-dep-ve-gia-dinh_035107328-1-100x75.jpg)


