
Cho ∆ABC vuông tại A, đường cao AH, biết \(AB = 15cm, BH = 9cm.\)
a. Tính AC, BC và đường cao AH
b. Gọi M là trung điểm của BC. Tính diện tích tam giác AHM

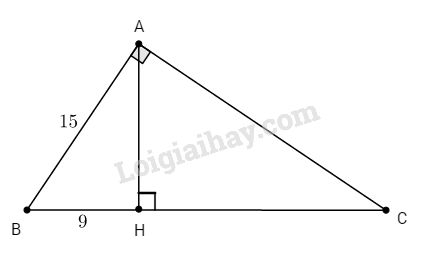
a. Ta có: ∆ABC vuông tại A, đường cao AH (gt)
\(A{B^2} = BC.BH\) (định lí 1)
Advertisements (Quảng cáo)
\( \Rightarrow BC = {{A{B^2}} \over {BH}}= {{{{15}^2}} \over 9} = 25\,\left( {cm} \right)\)
Theo định lí Pi-ta-go \(A{C^2} = B{C^2} – A{B^2}\)
\( \Rightarrow AC = \sqrt {B{C^2} – A{B^2}} \)\(\;= \sqrt {{{25}^2} – {{15}^2}} = 20\,\left( {cm} \right)\)
Lại có: AB.AC = BC.AH (định lí 3)
Advertisements (Quảng cáo)
\( \Rightarrow AH = {{AB.AC} \over {BC}} = {{15.20} \over {25}} = 12\,\left( {cm} \right)\)
b. M là trung điểm của BC (giả thiết)
\( \Rightarrow MB = MC = {{BC} \over 2} = {{25} \over 2} \)\(\:= 12,5\,\left( {cm} \right) \)
\(\Rightarrow MH = MB – BH = 12,5 – 9\)\(\; = 3,5\,\left( {cm} \right) \)
Vậy \({S_{AHM}} = {1 \over 2}MH.AH = {1 \over 2}.3,5.12 \)\(\;= 21\,\left( {c{m^2}} \right)\)






