Đề thi và đáp án đề kiểm tra, khảo sát chất lượng đầu năm lớp 9 Toán năm 2015 – Trường THCS Xuân Lai – Gia Bình – Bắc Ninh.
Câu 1 ( 3 điểm ) :
1/ Tính giá trị của biểu thức x2 – 1 tại x = 10
2/ Phân tích các đa thức sau thành nhân tử :
a) x2 – 2x b) 2(x – y ) – y(x – y )
Câu 2 ( 2 điểm ) : Giải các phương trình sau :
a) x – 2 = 11 b) (x – 2)(x + 3) = 0
Advertisements (Quảng cáo)
Câu 3 (1,5 điểm ) : Giải bài toán sau bằng cách lập phương trình :
Một người đi xe đạp từ A đến B với vận tốc trung bình 15 km/h. Lúc về người đó đi với vận tốc 12 km/h nên thời gian về nhiều hơn thời gian đi là 45 phút. Tính quãng đường AB.
Câu 4 ( 3 điểm ) :
Advertisements (Quảng cáo)
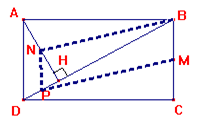
Cho hình chữ nhật ABCD có AB = 12 cm, BC = 9 cm. Gọi H là chân đường vuông góc kẻ từ A xuống BD.
a) Chứng minh : ∆HAD ∼∆CDB.
b) Tính độ dài đoạn thẳng AH.
c) Gọi M, N, P lần lượt là trung điểm của BC, AH, DH. Tứ giác BMPN là hình gì? vì sao?.
Câu 5 ( 0,5 điểm ): Cho x ≥ 0. Tìm giá trị nhỏ nhất của biểu thức :
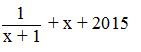
ĐÁP ÁN ĐỀ THI KHẢO SÁT ĐẦU NĂM
NĂM HỌC 2015-2016
Môn: Toán 9
| Câu | Nội dung | Điểm |
| 1(3đ) | 1/ Tính giá trị biểu thức:
Thay x = 10 vào biểu thức x2 – 1 ta được: 102 – 1 = 100 – 1 = 99 Vậy giá trị của biểu thức x2 – 1 bằng 99 tại x = 10. |
0,25đ
0,5đ 0,25đ |
| 2/ Phân tích đa thức thành nhân tử :
a) x2 – 2x = x(x – 1 ) b) 2(x – y ) – y(x – y ) = (x – y )(2 – y ) |
1đ
1đ |
|
| 2 (2đ) | a) x – 2 = 11 ⇔ x = 2 + 11⇔ x = 13 Vậy phương trình có tập nghiệm : S = . b) (x – 2)(x + 3) = 0 Vây phương trình có tập nghiệm : S = |
0,5đ
0,25đ 0,25đ 0,5đ 0,25đ 0,25đ |
| 3(1,5đ) | Đổi 45 phút = 3/4 ( giờ )
Gọi độ dài quãng đường AB là x ( x>0, km ) Thời gian người xe đạp đi từ A đến B là: x/15 ( giờ ) Thời gian người xe đạp đi từ B về A là: x/12 ( giờ ) Vì thời gian về nhiều hơn thời gian đi là 3/4 ( giờ ), nên ta có phương trình:
⇔5x-4x=45 ⇔x=45 x = 45 thỏa mãn điều kiện của ẩn. Vậy quãng đường AB dài 45 km. |
0,25đ
0.25đ 0,25đ 0,25đ 0,25đ 0,25đ
|
| 4(3đ) | – Hình vẽ đúng và ghi GT-KL
a) Xét ∆HAD và ∆CDB có: Góc AHD= Góc DCB=90 và Góc ADH=DBC (So le trong).Vậy ∆HAD ∼ ∆CDB (g-g). b) – Tính BD = 15cm – Tính AH = 7,2cm c) Chứng minh được tứ giác BMPN là hình bình hành |
0,5đ
1đ 0,5đ 0,5đ 0,5đ |
| 5(0,5đ) |
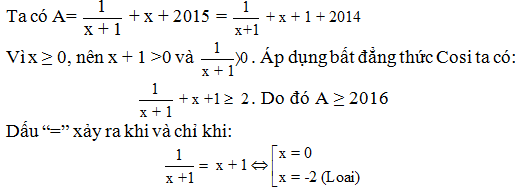 Vậy giá trị nhỏ nhất của A = 2016 khi x = 0 |
0,25đ 0,25đ |
