Đề và đáp án khảo sát chất lượng đầu năm Toán lớp 9 năm 2015 Thanh Oai – Hà Nội. Đề thi gồm 4 câu, thang điểm 10. Thời gian làm bài 90 phút.
| PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HUYỆN THANH OAI ĐỀ CHÍNH THỨC |
ĐỀ KHẢO SÁT CHẤT LƯỢNG LỚP 9
ĐẦU NĂM HỌC 2015- 2016 Môn : TOÁN Thời gian: 90 phút (Không kề thời gian phát đề) |
1 (3,0 điểm): Giải các phương trình sau:
a) 3x + 2 =2x – 5
b) (2x+1)(x-1) = 0.

2 (2,0 điểm): Giải các bất phương trình sau:
a. 2(3x-1) < 2x + 4.
Advertisements (Quảng cáo)
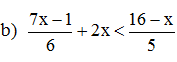
3 (2,0 điểm):
Một người đi xe đạp từ A đến B với vận tốc 15km/h. Lúc về, người đó chỉ đi với vận tốc là 12km/h, nên thời gian về nhiều hơn thời gian đi là 45 phút. Tính độ dài quãng đường AB.
Advertisements (Quảng cáo)
4 (3,0 điểm)
Cho tam giác ABC vuông ở A, có AB = 6cm; AC = 8cm. Vẽ đường cao AH và phân giác AD của góc A (D BC) .
a. Tính BC.
b. Chứng minh AB2 = BH.BC.
c. Tính BH, BD.
HƯỚNG DẪN CHẤM KIỂM TRA CHẤT LƯỢNG LỚP 9
ĐẦU NĂM HỌC 2015 – 2016:
MÔN TOÁN
| 1 | Hướng dẫn giải | Điểm |
|
(3 điểm)
|
a.Ta có: 3x + 2 =2x – 5 ⇔ 3x – 2x = –2 – 5 ⇔ x= -7 | 0,75 |
| Vậy phương trình đã cho có nghiệm duy nhất x = -7. | 0,25 | |
| b.Ta có: (2x+1)(x-1) = 0 ⇔ 2x+1=0 hoặc x-1=0 | 0,25 | |
| ⇔x =-1/2 hoặc x = 1 | 0,5 | |
| Vậy tập nghiệm của phương trình đã cho là S= {-1/2; 1} | 0,25 | |
| c. ĐKXĐ: x≠3 và x≠1 | 0,25 | |

⇔ 2(x-1)+(x-5)(x-3) = (x-1)(x-3) |
0,25 | |
| ⇔2x -2 + x2 -8x +15 = x2– 4x+3
⇔-2x = -10 ⇔x = – 5 (TMĐK) |
0,25
|
|
| KL: …… | 0,25 | |
| 2
(2 điểm) |
a) 2(3x-1) < 2x + 4 ⇔ 6x – 2 < 2x + 4 | 0,25 |
| 4x < 6 ⇔ x < 3/2 | 0,5 | |
| KL: …. | 0,25 | |
| b) |
0,25 | |
| ⇔ 35x – 5 + 60x < 96 – 6x ⇔ 101x < 101 ⇔x < 1 | 0,5 | |
| KL ….. | 0,25 | |
| 3 (2 điểm) | Đổi: 45 phút = 3/4 giờ.
Gọi độ dài quãng đường AB là (km), ĐK: x > 0 Thời gian người đi xe đạp đi từ A đến B là: x/15 (giờ) Thời gian người đi xe đạp đi từ A đến B là: x/12 (giờ) |
0,5
0,5 |
| Theo bài ta có pt: x/12 – x/15 = 3/4
Giải phương trình (*) tìm được x = 45 (thoả mãn điều kiện x > 0) |
0,25 0,5 |
|
| Vậy độ dài quãng đường AB là 45 km. | 0,25 | |
| 4
(3 điểm)
|
Hình vẽ:
|
|
| a) Áp dụng định lý Pitago trong tam giác vuông ABC, ta có:
BC2 =AB2 +AC2 =62 + 82 =100 ⇒BC= 10 (cm) |
0,75 | |
| Vậy BC = 10 cm | 0,25 | |
| b) Xét ΔBAC và ΔBHA Có
∠BAC = ∠BHA = 900 Góc ∠ABC chung ⇒ ΔBAC ∼ ΔBHA |
0,5 | |
| nên BA/BH = BC/BA ⇒ AB.AB = BH.BC AB2 = BH.BC | 0,25 | |
| Vậy AB2 = BH.BC. | 0,25 | |
| c) Theo câu b, AB2 = BH.BC ⇒ BH = AB2/BC =62/10 = 3,6 (cm)
* Vì AD là tia phân giác của góc nên, ta có: BD/AB =CD/AC (t/chất) + Áp dụng TC của dãy tỉ số bằng nhau ta có:
|
0,25 0,25 0,25 |
|
| Vậy BH = 3,6 (cm), BD = 30/7 (cm). | 0,25 |
Tải về máy tính:De thi khao sat dau nam toan 9 2015- 2016 -dethikiemtra.com


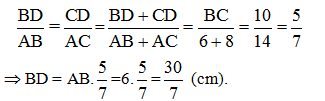

![[Trường THCS Nguyễn Du] Thi cuối kì 2 môn Anh lớp 9: Kangaroos, which come…Australia, have long tails](https://dethikiemtra.com/wp-content/uploads/2015/08/mon-tieng-anh-lop-9-100x75.jpg)



