Cho đường tròn đường kính BC cố định và \(BC = 2R.\) Lấy điểm A di động trên đường tròn (A khác B và C).
a. Chứng minh rằng ∆ABC là tam giác vuông
b. Chứng minh rằng : \({S_{ABC}} \le {R^2}.\)
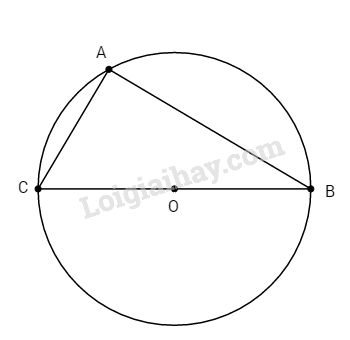
a. Ta có: \(OA = OB = OC (= R)\) \( \Rightarrow OA = {{BC} \over 2}\)
Advertisements (Quảng cáo)
Trong ∆ABC, AO là đường trung tuyến và \(AO = {{BC} \over 2}\) nên ∆ABC vuông tại A.
b. Kẻ đường cao AH của tam giác ABC.
Ta có: \({S_{ABC}} = {1 \over 2}BC.AH \)\(\;= {1 \over 2}.2R.AH = R.AH\)
Advertisements (Quảng cáo)
Trong tam giác vuông AHO, ta có:
\(AH ≤ AO\) (cạnh góc vuông < cạnh huyền)
hay \(AH ≤ R\) \( \Rightarrow AH.R \le {R^{2.}}\) Vậy \({S_{ABC}} \le {R^2}\)
Dấu “=” xảy ra khi A trùng với các đầu mút của đường kính vuông góc với BC.
Chú ý : Từ kết quả trên bạn có thể xét bài toán : “Tìm vị trí của điểm A để diện tích ∆ABC lớn nhất”.
