
Cạnh huyền của một tam giác vuông là 10cm, các cạnh góc vuông tỉ lệ với 4 và 3. Tính độ dài hình chiếu của mỗi cạnh góc vuông lên cạnh huyền.

Theo bài ra, ta có: \({b \over c} = {4 \over 3} \Rightarrow {b \over 4} = {c \over 3}\)
\(\eqalign{ & \Rightarrow {{{b^2}} \over {16}} = {{{c^2}} \over 9} = {{{b^2} + {c^2}} \over {16 + 9}} = {{{a^2}} \over {25}} \cr&\;\;\;\;\;\;\;\;\;\;\;= {{{{10}^2}} \over {25}} = 4 \cr & \Rightarrow {b^2} = 4.16 \Rightarrow b = 8\,\left( {cm} \right) \cr} \)
Advertisements (Quảng cáo)
Tương tự : \(c = 6cm\)
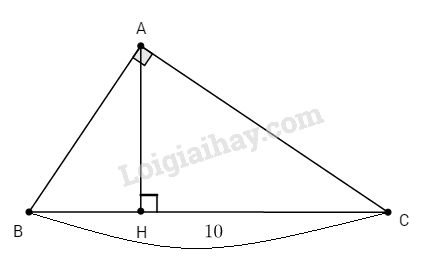
\(∆ABC\) vuông tại A, đường cao AH.
Ta có: \({b^2} = a.b’\) (định lí 1) \( \Rightarrow b’ = {{{b^2}} \over a} = {{{8^2}} \over {10}} = 6,4\,\left( {cm} \right)\)
Do đó: \(c’ = a – b’ = 10 – 6,4 = 3,6\,\left( {cm} \right)\)
Advertisements (Quảng cáo)
Cách khác: Đặt \(b = 4k, c = 3k\) (vì \({b \over 4} = {c \over 3} = k\)), ta có:
\(\eqalign{ & {\left( {4k} \right)^2} + {\left( {3k} \right)^2} = {10^2} \cr&\Leftrightarrow 16{k^2} + 9{k^2} = 100 \cr & \Leftrightarrow 25{k^2} = 100\cr& \Leftrightarrow {k^2} = 4 \Leftrightarrow k = 2 \cr} \)
Do đó: \(b = 4.2 = 8\; (cm)\) và \(c = 3.2 = 6\; (cm)\).






