Đề kiểm tra 15 phút lớp 9 môn Toán Chương 3 Hình học: Chứng minh tứ giác EHKF nội tiếp

Trên các cạnh BC và CD của hình vuông ABCD lấy các điểm E và F sao cho \(\widehat {EAF} = 45^\circ \) . Các đoạn thẳng AE, AF cắt BD theo thứ tự ở H và K. Chứng minh tứ giác EHKF nội tiếp.

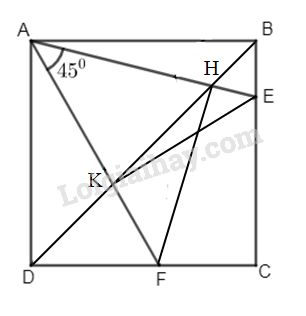
Ta có \(\widehat {EAF} = \widehat {BDC} = 45^\circ \)

Hai điểm A và D ở cùng phía với HF nên AD thuộc cung chứa góc 45º vẽ trên đoạn HF.

Hay bốn điểm A, D, F, H cùng thuộc một đường tròn nên tứ giác ADFH nội tiếp

\( \Rightarrow \widehat {ADF} + \widehat {AHF} = 180^\circ \) mà \(\widehat {ADF} = 90^\circ  \)

\(\Rightarrow \widehat {AHF} = 90^\circ  \Rightarrow \widehat {FHE} = 90^\circ .\)

Chứng minh tương tự ta có \(\widehat {FKE} = 90^\circ \). Do đó EHKF là tứ giác nội tiếp.