
Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A và B. Gọi M là điểm tùy ý trên đường thẳng AB, nằm ngoài đoạn AB. Vẽ qua M hai cát tuyến MCD và MC’D’ với (O) và (O’). Chứng minh tứ giác CDD’C’ nội tiếp.

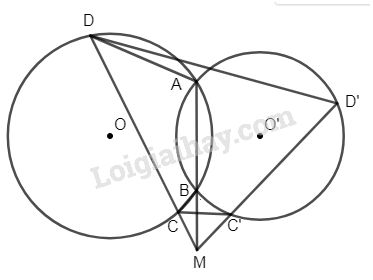
Ta có tứ giác ABCD nội tiếp trong đường tròn (O) nên \(\widehat {CDA} = \widehat {CBM}\) ( cùng bù với \(\widehat {ABC}\)).
Do đó \(∆MBC\) đồng dạng \(∆MDA \) (g.g)
Advertisements (Quảng cáo)
\( \Rightarrow \dfrac{{MA}}{{MC}} =\dfrac {{MD} }{ {MB}}\)
\( \Rightarrow MA.MB = MC.MD\)
Chứng minh tương tự :
\(MA.MB = MC’.MD’\)
Advertisements (Quảng cáo)
\( \Rightarrow MC.MD = MC’.MD’\)
Do đó \(∆MCC’\) đồng dạng \(∆MD’D\) (g.g)
\( \Rightarrow \widehat {MCC’} = \widehat {MD’D}\)
Vậy tứ giác CDD’C’ nội tiếp.






