
Bài 1. Cho \(∆ABC\) vuông tại A và \(\widehat B = \alpha .\) Chứng minh rằng:
a. \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
b. \(\tan \alpha = {{\sin \alpha } \over {\cos \alpha }}\)
Bài 2. Hãy sắp xếp các tỉ số lượng giác sau đây theo thứ tự tăng dần (không dùng bảng số và máy tính) :
a. \(\sin 40^\circ ,\,\cos 28^\circ ,\,\sin 65^\circ ,\,\cos 88^\circ \)
b. \(\tan 65^\circ ,\cot 42^\circ ,\tan 76^\circ ,\cot 27^\circ .\)

Bài 1.
Advertisements (Quảng cáo)
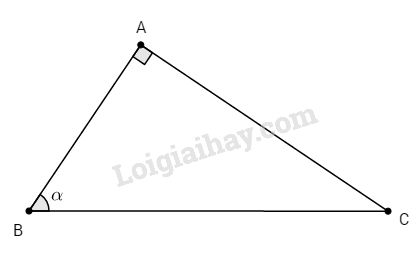
a. Theo định nghĩa ta có: \(\sin \alpha = {b \over a} \Rightarrow {\sin ^2}\alpha = {{{b^2}} \over {{a^2}}}\)
\(\cos \alpha = {c \over a} \Rightarrow {\cos ^2}\alpha = {{{c^2}} \over {{a^2}}}\)
Do đó: \({\sin ^2}\alpha + {\cos ^2}\alpha = {{{b^2} + {c^2}} \over {{a^2}}} = {{{a^2}} \over {{a^2}}} = 1\)
b. \(\tan \alpha = {b \over c} = {b \over c}:{c \over a} = {{\sin \alpha } \over {\cos \alpha }}\)
Advertisements (Quảng cáo)
Bài 2. a. Ta có:
\(\eqalign{ & \cos 28^\circ = \sin \left( {90^\circ – 28^\circ } \right) = \sin 62^\circ \cr & \cos 88^\circ = \sin \left( {90^\circ – 88^\circ } \right) = \sin 2^\circ \cr} \)
Mà \(\sin 2^\circ < \sin 40^\circ < \sin 62^\circ < \sin 65^\circ \) (góc tăng thì sin tăng)
\( \Rightarrow \cos 88^\circ < \sin 40^\circ < \cos 28^\circ \)\(\, < \sin 65^\circ .\)
b. Ta có:
\(\eqalign{ & \cot 42^\circ = \tan \left( {90^\circ – 42^\circ } \right) = \tan 48^\circ \cr & \cot 27^\circ = \tan \left( {90^\circ – 27^\circ } \right) = \tan 63^\circ \cr} \)
Mà \( \tan 48^\circ < \tan 63^\circ < \tan 65^\circ < \tan 76^\circ \)
\(\Rightarrow \cot 42^\circ < \cot 27^\circ < \tan 65^\circ\)\(\, < \tan 76^\circ \)

![[TX An Nhơn] thi học kì 2 lớp 9 môn Văn năm 2020: Tác phẩm “Những ngôi sao xa xôi” được Lê Minh Khuê viết vào năm nào?](https://dethikiemtra.com/wp-content/uploads/2020/06/canh-dong-100x75.jpg)



