Tóm tắt kiến thức và hướng dẫn giải bài 67,68,69 sgk trang 36 toán đại số 9 tập 1: Căn bậc ba (căn bậc 3).
Tóm tắt kiến thức:
1. Căn bậc ba của một số a là số x sao cho x3 = a
Căn bậc ba của số a được kí hiệu là 3√a
Như vậy (3√a)3 = a
Mọi số thực đều có căn thức bậc ba.
2. Các tính chất:
a) a < 3√a < 3√b
b) 3√ab = 3√a. 3√b;
c) Với b#0, ta có 3√(a/b) = 3√a / 3√b
3. Từ các tính chất trên, ta cũng có các quy tắc đưa thừa số vào trong, ra ngoài dấu căn bậc ba, quy tắc khử mẫu của biểu thức lấy căn bậc ba và quy tắc trục căn bậc ba ở mẫu:
Advertisements (Quảng cáo)
a) a3√b = 3√a3b
b)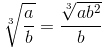 
c) Áp dụng hằng đẳng thức 
ta có
Do đó
Hướng dẫn giải bài tập Toán 9 đại số tập 1 trang 36
Bài 67. Hãy tìm: 3√512; 3√-729; 3√-0,216; 3√-0,008
Phân tích số dưới dấu căn ra thừa số nguyên tố hoặc đổi thành phân số.
3√512 = 3√29 = 3√(23)3= 23 = 8
3√-729 = – 3√729 = – 3√36=- 3√(32)3 = – (32)= -9
Advertisements (Quảng cáo)
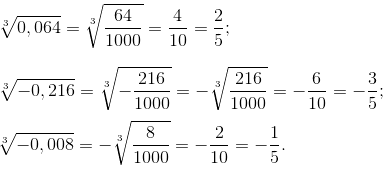
Bài 68 trang 36. Tính
a) 3√27 – 3√-8 – 3√125
b)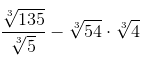 
ĐS: a) 3√27 – 3√-8 – 3√125 = 3√33 – 3√(-2)3 – 3√53 = 3 – (-2) – 5 = 0
b) =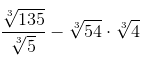
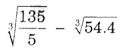
= √27 – 3√216 = 3√33 – 3√(6)3 = 3 – 6 = -3
Bài 69. So sánh:
a) 5 và 3√123; b) 53√6 và 63√5
Giải: a) 5 và 3√123:
Ta có 5 = 3√125; vì 125 > 123 ⇒ 3√125 > 3√123.Vậy 5 > 3√123
b) Ta có:
53√6 = 3√53.6 = 3√125.6 = 3√750
63√5 = 3√63.5 = 3√216.5 = 3√1080
Vì 750 < 1080 ⇒3√750 < 3√1080 . Vậy 53√6 < 63√5.
