Tóm tắt lý thuyết và Giải bài 4,5,6 trang 11; bài 7,8,9,10,11 trang 12 SGK Toán 9 tập 2: Hệ hai phương trình bậc nhất hai ẩn.
1. Khái niệm về hệ phương trình bậc nhất hai ẩn:
Hệ hai phương trình bậc nhất hai ẩn có dạng: (I) ![]() trong đó ax + by = c và a’x + b’y = c’ là những phương trình bậc nhất hai ẩn. Nếu hai phương trình của hệ có nghiệm chung thì nghiệm chung ấy gọi là nghiệm của hệ phương trình (I). Trái lại, nếu hai phương trình không có nghiệm chung thì ta nói hệ (I) là vô nghiệm.
trong đó ax + by = c và a’x + b’y = c’ là những phương trình bậc nhất hai ẩn. Nếu hai phương trình của hệ có nghiệm chung thì nghiệm chung ấy gọi là nghiệm của hệ phương trình (I). Trái lại, nếu hai phương trình không có nghiệm chung thì ta nói hệ (I) là vô nghiệm.
Giải hệ phương trình là tìm tất cả các nghiệm của nó.
2. Minh họa hình học tập nghiệm của hệ phương trình bậc nhất hai ẩn.
Đối với hệ phương trình (I), ta có:
Nếu (d) cắt (d’) thì hệ (I) có một nghiệm duy nhất.
Nếu (d) song song với (d’) thì hệ (I) vô nghiệm.
Nếu (d) trùng với (d’) thì hệ (I) có vô số nghiệm.
3. Hệ phương trình tương đương:
Hai hệ phương trình được gọi là tương đương với nhau nếu chúng có cùng tập nghiệm.
Hướng dẫn giải bài Hệ hai phương trình bậc nhất hai ẩn – Toán 9 tập 2 SGK trang 11, 12
Bài 4. Không cần vẽ hình, hãy cho biết số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao:
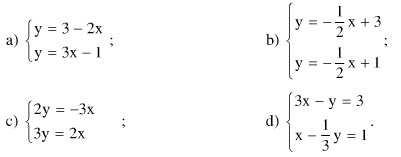

a)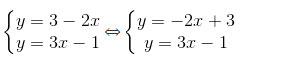
Ta có a = -2, a’ = 3 nên a ≠ a’ => Hai đường thẳng cắt nhau.
Vậy hệ phương trình có một nghiệm (vì hai đường thẳng có phương trình đã cho trong hệ là hai đường thẳng có hệ số góc khác nhau nên chúng cắt nhau tại một điểm duy nhất).
b) 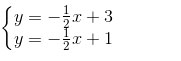 Có a =-1/2, a’ =-1/2, b = 3, b’ = 1 nên a = a’, b ≠ b’.
Có a =-1/2, a’ =-1/2, b = 3, b’ = 1 nên a = a’, b ≠ b’.
⇒ Hai đường thẳng song song.
Vậy hệ phương trình vô nghiệm (vì hai đường thẳng có phương trình đã cho trong hệ là hai đường khác nhau và cso cùng hệ số góc nên chúng song song với nhau).
c)
Có a =-3/2, a’ =2/3 nên a ≠ a’ => Hai đường thẳng cắt nhau.
Vậy hệ phương trình có một nghiêm.
d)
Có a = 3, a’ = 3, b = -3, b’ = -3 nên a = a’, b = b’.
⇒ Hai đường thẳng trùng nhau.
Vậy hệ phương trình có vô số nghiệm (vì hai đường thẳng có phương trình đã cho trong hệ trùng nhau).
Bài 5 trang 11 Toán 9 tập 2
Đoán nhận số nghiệm của hệ phương trình sau bằng hình học:

Đáp án 5:
a) 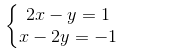 Vẽ (d1): 2x – y = 1
Vẽ (d1): 2x – y = 1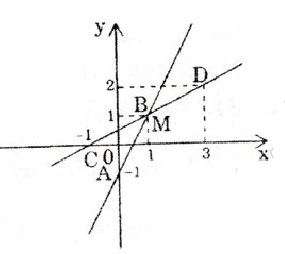
Cho x = 0 => y = -1, ta được A(0; -1).
Cho y = 1 => x = 1, được B(1;1).
Vẽ (d2): x – 2y = -1
Advertisements (Quảng cáo)
Cho x = -1 => y = 0 , được C (-1;0).
Cho y = 2 => x = 3, được D = (3; 2).
Hai đường thẳng cắt nhau tại điểm M có tọa độ (x = 1, y = 1).
Thay x = 1, y = 1 vào các phương trình của hệ ta được:
2 . 1 – 1 = 1 (thỏa mãn)
1 – 2 . 1 = -1 (thỏa mãn)
Vậy hệ phương trình có một nghiệm (x; y) = (1; 1).
b) 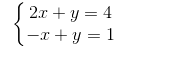 Vẽ (d1): 2x + y = 4
Vẽ (d1): 2x + y = 4
Cho x = 0 => y = 4, được A(0; 4).
Cho y = 0 => x = 2, được B(2; 0).
Vẽ (d2): -x + y = 1
Cho x = 0 => y = 1, được C(0; 1).
Cho y = 0 => x = -1, được D(-1; 0).
Hai đường thẳng cắt nhau tại điểm N có tọa độ (x = 1; y = 2).
Thay x = 1, y = 2 vào các phương trình của hệ ta được:
2 . 1 + 2 = 4 và -1 + 2 = 1 (thỏa mãn)
Vậy hệ phương trình có một nghiệm (x; y) = (1; 2).
Bài 6. Đố: Bạn Nga nhận xét: Hai hệ phương trình bậc nhất hai ẩn vô nghiệm thì luôn tương đương với nhau. Bạn Phương khẳng định: Hai hệ phương trình bậc nhất hai ẩn cùng có vô số nghiệm thì cũng luôn tương đương với nhau.
Theo em, các ý kiến đó đúng hay sai ? Vì sao ? (có thể cho một ví dụ hoặc minh họa bằng đồ thị).
Lời giải: Bạn Nga đã nhận xét đúng vì hai hệ phương trình cùng vô nghiệm có nghĩa là chũng cùng có tập nghiệm bằng Φ.
Bạn Phương nhân xét sai. Chẳng hạn, hai hệ phương trình:
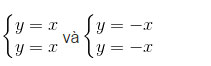
Advertisements (Quảng cáo)
đều có vô số nghiệm nhưng tập nghiệm của hệ thứ nhất được biểu diễn bởi đường thẳng y = x, còn tập nghiệm của phương trình thứ hai được biểu diện bởi đường thẳng y = -x. Hai đường thẳng này là khác nhau nên hai hệ đang xét không tương đương (vì không có cùng tập nghiệm).
Giải bài 7,8,9,10,11 trang 12 Luyện tập Hệ hai phương trình bậc nhất hai ẩn
Bài 7. Cho hai phương trình 2x + y = 4 và 3x + 2y = 5.
a) Tìm nghiệm tổng quát của mỗi phương trình trên.
b) Vẽ các đường thẳng biểu diễn tập nghiệm của hai phương trình trong mỗi một hệ trục tọa độ, rồi xác định nghiệm chung của chúng.
Lời giải: a) 2x + y = 4 ⇔ y = -2x + 4 ⇔ x = -1/2y + 2. Do đó phương trình có nghiệm dạng tổng quát như sau:
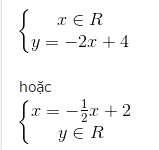
b) Vẽ (d1): 2x + y = 4
– Cho x = 0 => y = 4 được A(0; 4).
– Cho y = 0 => x = 2 được B(2; 0).
Vẽ (d2): 3x + 2y = 5
– Cho x = 0 => y = 5/2 được C(0;5/2).
– Cho y = 0 => x =5/3 được D(5/3; 0).
Hai đường thẳng cắt nhau tại M(3; -2).
Thay x = 3, y = -2 vào từng phương trình ta được:
2 . 3 + (-2) = 4 và 3 . 3 + 2 . (-2) = 5 (thỏa mãn)
Vậy (x = 3; y = -2) là nghiệm chung của các phương trình đã cho.
Bài 8. Cho các hệ phương trình sau:
Giải: Trước hết, hãy đoán nhận số nghiệm của mỗi hệ phương trình trên (giải thích rõ lí do). Sau đó, tìm tập nghiệm của các hệ đã cho bằng cách vẽ hình.
a)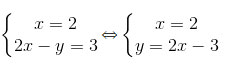
Hệ có nghiệm duy nhất vì một đồ thị là đường thẳng x = 2 song song với trục tung, còn một đồ thị là đường thẳng y = 2x – 3 cắt hai trục tọa độ.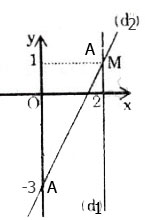
Vẽ (d1): x = 2
Vẽ (d2 ): 2x – y = 3
– Cho x = 0 => y = -3 được A(0; -3).
– Cho y = 1 => x = 2 được B(2;1)
Ta thấy hai đường thẳng cắt nhau tại M(2; 1).
Vậy hệ phương trình có nghiệm (2; 1).
b)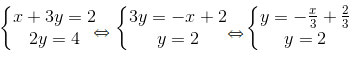
Hệ có nghiệm duy nhất vì một đồ thị là đường thẳng y =-x/3 +2/3 cắt hai trục tọa độ, còn một đồ thị là đường thẳng y = 2 song song vơi trục hoành.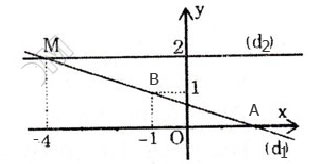
Vẽ (d1): x + 3y = 2
– Cho x = 2 => y = 0 được A(2;0)
– Cho y = 1 => x = -1 được B(-1; 1).
Vẽ (d2): y = 2
Ta thấy hai đường thẳng cắt nhau tại M(-4; 2).
Thay x = -4, y = 2 vào phương trình x + 3y = 2 ta được -4 + 3 . 2 = 2 (thỏa mãn).
Vậy hệ phương trình có nghiệm (-4; 2).
Bài 9 trang 12. Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:

Giải: a)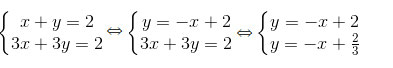
Ta có: a = -1, a’ = -1, b = 2, b’ = 2/3 nên a = a’, b ≠ b’ => Hai đường thẳng song song nhau.
Vậy hệ phương trình vô nghiệm vì hai đường thẳng biểu diễn các tập nghiệm của hai phương trình trong hệ song song với nhau.
b)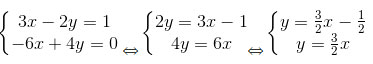
Ta có: a = 3/2, a’ =3/2, b = -1/2, b’ = 0 nên a = a’, b ≠b’.
=> Hai đường thẳng song song với nhau.
Vậy hệ phương trình vô nghiệm vì hai đường thẳng biểu diễn các tập nghiệm của hai phương trình trong hệ song song với nhau.
Bài 10. Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:

Đáp án: a)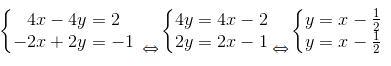
Ta có:
a = a’ = 1, b = b’ = -1/2=> Hai đường thẳng trùng nhau.
Vậy hệ phương trình có vô số nghiệm vì hai đường thẳng biểu diễn các tập nghiệm của hai phương trình trong hệ là trùng nhau.
b)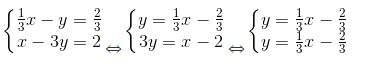
Ta có a = a’ =1/3, b = b’ = -2/3 nên hai đường thẳng trùng nhau.
Vậy hệ phương trình có vô số nghiệm.
Bài 11. Nếu tìm thấy hai nghiệm phân biệt của một hệ hai phương trình bậc nhất hai ẩn (nghĩa là hai nghiệm được biểu diễn bởi hai điểm phân biệt) thì ta có thể nói gì về số nghiệm của hệ phương trình đó ? Vì sao ?
Nếu tìm thấy hai nghiệm phân biệt của một hệ phương trình bậc nhất hai ẩn thì ta có thể kết luận hệ phương trình có vô số nghiệm, vì hệ có hai nghiệm phân biệt nghĩa là hai đường thẳng biểu diễn tập nghiệm của chúng có hai điểm chung phân biệt, suy ra chúng trùng nhau.



![[Phòng GD Cam Ranh] kiểm tra cuối năm lớp 9 môn Hóa: Tính thể tích và khối lượng rượu nguyên chất đã tham gia phản ứng?](https://dethikiemtra.com/wp-content/uploads/2020/09/hinh-anh-thay-co-y-nghia_015649704-100x75.jpg)


