Tóm tắt lý thuyết và Giải bài 1,2,3 trang 7 SGK Toán 9 tập 2: Phương trình bậc nhất hai ẩn – Chương 3 Đại số 9: Hệ hai phương trình bậc nhất hai ẩn.
A. Tóm tắt lý thuyết bài phương trình bậc nhất hai ẩn
1. Khái niệm:
Phương trình bậc nhất hai ẩn x, y là hệ thức dạng:
ax + by = c (1)
Trong đó a, b và cc là các số đã biết (a ≠ b hoặc b ≠ 0).
2. Tập hợp nghiệm của phương trình:
a) Một nghiệm của phương trình (1) là một cặp số
(x0, y0) sao cho ax0 + by0 = c.
b) Phương trình bậc nhất hai ẩn ax + by = c luôn có vô số nghiệm. Tập nghiệm của nó được biểu diễn bởi đường thẳng ax + by = c,
kí hiệu là (d).
– Nếu a ≠ 0 và b ≠ 0 thì công thức nghiệm là:
hoặc 
Khi đó đường thẳng (d) cắt cả hai trục tọa độ.
– Nếu a = 0, b ≠ 0 thì công thức nghiệm là:
và (d) // Ox
– Nếu a ≠ 0, b = 0 thì công thức nghiệm là:
và (d) // Oy.
B. Hướng dẫn giải bài Phương trình bậc nhất hai ẩn Toán 9 tập 2 SGK trang 7
Bài 1. Trong các cặp số (-2; 1), (-1; 0), (1,5; 3) và (4; -3), cặp số nào là nghiệm của phương trình:
a) 5x + 4y = 8 ? b) 3x + 5y = -3 ?
Giải: a) Thay từng cặp số đã cho vào phương trình 5x + 4y = 8, ta được:
– 5(-2) + 4 . 1 = -10 + 4 = -6 ≠ 8 nên cặp số (-2; 1) không là nghiệm của phương trình.
– 5 . 0 + 4 . 2 = 8 nên cặp số (0; 2) là nghiệm của phương trình.
Advertisements (Quảng cáo)
– 5 . (-1) + 4 . 0 = -5 ≠ 8 nên (-1; 0) không là nghiệm của phương trình.
– 5 . 1,5 + 4 . 3 = 7,5 + 12 = 19,5 ≠ 8 nên (1,5; 3) không là nghiệm của phương trình.
– 5 . 4 + 4 . (-3) = 20 -12 = 8 nên (4; -3) là nghiệm của phương trình.
Vậy có hai cặp số (0; 2) và (4; 3) là nghiệm của phương trình 5x + 4y = 8.
b) Với phương trình 3x + 5y = -3:
– 3 . (-2) + 5 . 1 = -6 + 5 = -1 ≠ -3 nên (-2; 1) không là nghiệm của phương trình.
– 3 . 0 + 5 . 2 = 10 ≠ -3 nên (0; 2) không là nghiệm.
– 3 . (-1) + 5 . 0 = -3 nên (-1; 0) là nghiệm.
– 3 . 1,5 + 5 . 3 = 4,5 + 15 = 19,5 ≠ -3 nên (1,5; 3) không là nghiệm.
– 3 . 4 + 5 . (-3) = 12 – 15 = -3 nên (4; -3) là nghiệm.
Vậy có hai cặp số (-1; 0) và (4; -3) là nghiệm của phương trình 3x + 5y = -3.
Bài 2. Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó:
a) 3x – y = 2; b) x + 5y = 3;
c) 4x – 3y = -1; d) x +5y = 0;
e) 4x + 0y = -2; f) 0x + 2y = 5.
Advertisements (Quảng cáo)
Giải: a) 3x – y = 2
Nghiệm tổng quát: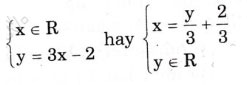
Vẽ đường thẳng biểu diễn tập nghiệm của phương trình: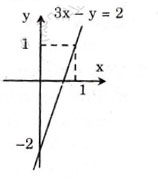
Với y = 3x – 2
Cho x = 0 => y = -2 được A(0; -2).
Cho x= 1 => y = 1 được B(1;1)
Biều diễn cặp số A(0; -2) và B(1;1) trên hệ trục tọa độ và đường thẳng AB chính là tập nghiệm của phương trình 3x – y = 2.
Tương tự các em làm các câu sau như câu a)
b) x + 5y = 3
Nghiệm tổng quát: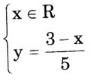
hay
Vẽ đường thẳng biểu diễn tập nghiệm của phương trình:
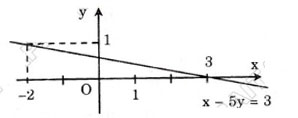
c) 4x – 3y = -1
Nghiệm tổng quát: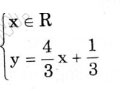
hay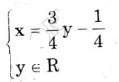
Vẽ đường thẳng biểu diễn tập nghiệm của phương trình: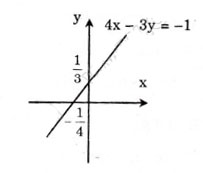
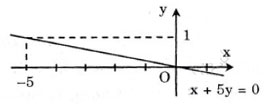
d) x + 5y = 0
Nghiệm tổng quát:
hay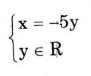
Vẽ đường thẳng biểu diễn tập nghiệm của phương trình:
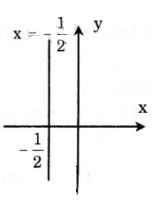
e) 4x + 0y = -2
Nghiệm tổng quát:
Vẽ đường thẳng biểu diễn tập nghiệm của phương trình:
f) 0x + 2y = 5.
Nghiệm tổng quát: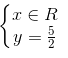
Vẽ đường thẳng biểu diễn tập nghiệm của phương trình:
Bài 3 trang 7. Cho hai phương trình x + 2y = 4 và x – y = 1. Vẽ hai đường thẳng biểu diễn tập nghiệm của hai phương trình đó trên cùng một hệ trục tọa độ. Xác định tọa độ giao điểm của hai đường thẳng và cho biết tọa độ của nó là nghiệm của các phương trình nào.
Hướng dẫn giải bài 3: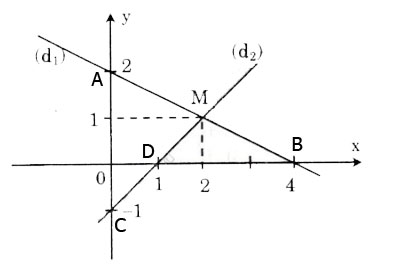
Vẽ đường thẳng x + 2y = 4.
– Cho x = 0 => y = 2 được A(0; 2).
– Cho y = 0 => x = 4 được B(4; 0).
Đường thẳng cần vẽ là đường thẳng (d1) đi qua A, B.
Vẽ đường thẳng x – y = 1.
– Cho x = 0 => y = -1 được C(0; -1).
– Cho y = 0 => x = 1 được D(1; 0).
Đường thẳng cần vẽ là đường thẳng (d2) đi qua C, D.
Giao điểm của hai đường thẳng có tọa độ là M (2; 1).
Ta có (2; 1) cùng thuộc hai đường thẳng nên nó là nghiệm của cả hai phương trình đã cho.
