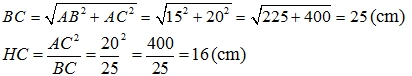[Đề toán 8 có đáp án] Thi học kỳ 2 môn Toán 8 – Tân Châu năm 2015 – 2016.
I. LÝ THUYẾT:
1: Phát biểu định nghĩa phương trình bậc nhất một ẩn? Cho 2 ví dụ.
2: Nêu định lý về trường hợp đồng dạng thứ ba (góc – góc) của hai tam giác? Vẽ hình, ghi giả thuyết, kết luận của định lí đó.
II. BÀI TẬP
1 GPT:a) 10 – 4x = 2x – 3;
![]()
c) | 2x -1| = 3
2: Giải BPT và biểu diễn tập nghiệm trên trục số:
3x + 4 >2x – 3
3 :Một người đi xe đạp từ A đến B với vận tốc 12km/h. Lúc về người đó đi với vận tốc 10km/h nên thờigian về nhiều hơn thờigian đi là 45 phút. Tính chiều dài quãng đường AB.
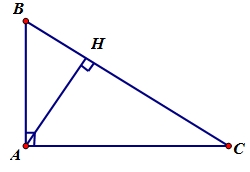
4 Cho tam giác ABC vuông tại A, có AB = 15cm, AC = 20cm. Vẽ đường cao AH (H∈BC).
a/ Chứng minh rằng ΔHBA ~ ΔABC.
b/ Chứng minh rằng AC² = BC.HC
c/ Tính độ dài các đoạn thẳng BC, HC.
ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI
BÀI TẬP
1.
| a) 10 – 4x = 2x – 3 |
| <=> – 4x – 2x = – 3 – 10 |
| <=> – 6x = -13 |
| <=> x = 13/6 |
| Vậy tập nghiệm S = { 13/6 } ( 1 điểm) |
![]()
Điều kiện: x ≠ 3/2 ; x ≠ 0
=> x – 3 = 5(2x – 3)
Advertisements (Quảng cáo)
<=> x – 3 = 10x – 15
<=> x – 10x = – 15 + 3
<=> x – 10x = – 15 + 3
<=> x = 4/3 ( TMĐK)
Vậy tập nghiệm của PT là: S = { 4/3 }
c) | 2x – 1| = 3 (1)
Ta có | 2x – 1| = 2x – 1 khi 2x – 1 ≥ 0 hay x ≥ 1/2
| 2x – 1| = – (2x – 1) khi 2x – 1 < 0 hay x <1/2
Vậy để GPT (1), ta quy về giải hai pt sau:
* PT 2x – 1 = 3 với điều kiện x ≥ 1/2
Ta có 2x – 1 = 3
<=> 2x = 3 + 1
<=> x = 2 (TMĐK)
Advertisements (Quảng cáo)
* Pt – (2x – 1) = 3 với điều kiện x <1/2
Ta có – 2x + 1 = 3
<=> – 2x = 3 – 1
<=> x = -1 (TMĐK)
Vậy tập nghiệm của phươngtrình là : S = { – 1; 2 }
2. 3x + 4 > 2x – 3
<=> 3x – 2x > – 3 – 4
<=> x > – 7
Vậy nghiệm của bất phươngtrình là x > – 7
Biểu diễn tập nghiệm trên trục số
![]()
3. Ta có: 45 phút = ¾ giờ
Gọi x (km) là chiều dài quãng đường AB (x > 0)
Thời.gian đi là: x/12 giờ
Thời.gian về là: x/10 giờ
Vì thờ. gian về nhiều hơn thờigian đi là 3/4 giờ nên ta có phương trình sau:
![]()
GPT ta được: x = 45 ( TMĐK)
Vậy quãng đường AB có chiều dài là: 45 km
4. 
a) Xét ΔHBA và ΔABC có:
∠BHA = ∠BAC = 900 ( GT)
Góc B: Chung
Vậy ΔHBA ~ ΔABC (g.g)
b) Xét ΔHAC và ΔABC.có:
∠AHC = ∠BAC =900 ( GT)
Góc C : Chung
Vậy ΔHAC ~ ΔABC (g.g)
Suy ra:
![]()
c) Áp dụng định lí Pytago cho vuông tại A, ta có: