Trường THPT Ten Lơ Man tổ chức thi giữa học kì 1 môn Toán lớp 12 năm học 2019 – 2020, đề thi gồm 2 phần cụ thể dưới đây:
Câu 1: Kết luận nào sau đây về tính đơn điệu của hàm số y = 2x+1/x -1 là đúng?
A. Hàm số luôn nghịch biến trên R\{1}
B. Hàm số luôn nghịch biến trên (-∞;1) và (1;+∞)
C. Hàm số luôn đồng biến trên R\{1}
D. Hàm số luôn đồng biến trên (-∞;1) và (1;+∞)
Câu 2: Hỏi hàm số y = x³/3 – 3x² + 5x -2 nghịch biến trên khoảng nào?
A. (5;+∝) B. (2;3) C. (-∝;1) D. (1;5)
Câu 3: Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình bên. Hỏi hàm số có bao nhiêu điểm cực trị?
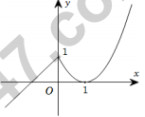
A. 0 B. 2 C. 3 D. 1
Câu 4: Cho hàm số y = -x³ + 3x. Hệ thức liên quan giữa giá trị cực đại Ycđ và giá trị cực tiểu Yct của hàm đã cho là
A. Yct = -Ycđ B. Yct = 3Ycđ C. Yct = Ycđ D. Yct = 2Ycđ
Câu 5: Số tiệm cận đứng của đồ thị hàm số y = 
là:
A. 3 B. 0 C. 2 D. 1
Câu 6: Đồ thị hàm số y = 
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
A. x = 1, x = 2 và y = 0 B. x = 1, x = 2 và y = 2
C. x= 1 và y = 0 D. x = 1, x = 2 và y = -3
Câu 7: Cho hàm số y = f(x) có đồ thị như hình bên. Giá trị nhỏ nhất của hàm số này trên đoạn [2;3] bằng:
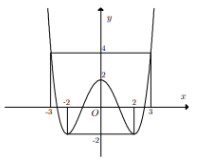
Advertisements (Quảng cáo)
A. -2 B. -3 C. 4 D. 0
Câu 8: Giá trị lớn nhất của hàm số y = x^4 – 4x² + 9 trên đoạn [-2;3] bằng:
A. 207 B. 20 C. 95 D. 54
Câu 11: Tiếp tuyến của đồ thị hàm số y = -x^4 + 8x² tại điểm có hoành độ bằng -3 có phương trình là:
A. y = 60x+171 B. y = -60x+171
C. 60x+189 D. 60x+189
Câu 12: Số giao điểm của đồ thị hàm số y = (x – 1)(x² -3x +2) và trục hoành là
A. 0 B. 1 C. 3 D. 2
Câu 13: Cho hàm số f(x) = ax^4 + bx² + c (a,b,c ∈ R). Đồ thị của hàm số y = f(x) như hình vẽ bên. Số nghiệm của phương trình 4f(x) – 3 = 0 là
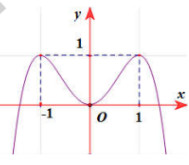
A. 4 B. 3 C. 2 D. 0
Advertisements (Quảng cáo)
Câu 14: Tìm giá trị nhỏ nhất của tham số m sao cho hàm số y = x³/3 +mx² – mx – m luôn đồng biến trên R?
A. m = -5 B. m = 0 C. m = -1 D. m = -6
Câu 15. Cho hình chóp S.ABC có đáy là tam giác đều. Nếu giảm độ dài cạnh đáy lên 2 lần và độ dài đường cao không đổi thì thể tích S.ABCgiảm lên bao nhiêu lần?
Câu 16. Cho hình chóp S.ABCD, có đáy ABCD là hình chữ nhật, SA vuông góc với (ABCD). Tính thể tích S.ABCD biết AB = 5a, AD = 2a, SA = 3a
