1. .Số mặt phẳng đối xứng của hình chóp đều \(S.ABC\) là
A. \(4\) .
B. \(2\) .
C. \(6\) .
D. \(3\) .
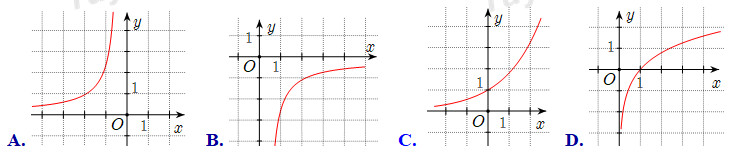
2. .Cho \(a\) là số thực dương khác \(1\) . Hình nào sau đây là đồ thị của hàm số mũ \(y = {a^x}\)?
3. . Khối cầu \((S)\) có bánh kính bằng \(r\) và thể tích bằng \(V\). Mệnh đề nào dưới đây đúng?
A. \(V = \dfrac{4}{3}\pi {r^3}\) .
B. \(V = \dfrac{4}{3}{\pi ^2}{r^2}\).
C. \(V = \dfrac{4}{3}{\pi ^2}{r^3}\).
D. \(V = \dfrac{4}{3}\pi r\).
4. . Cho \({\log _3}x = 6\). Tính \(K = {\log _3}\sqrt[3]{x}\).
A. \(K = 4\) .
B. \(K = 8\).
C. \(K = 2\).
D. \(K = 3\).
5. . Cho khối chóp \(S.ABCD\) có đáy là hình chữ nhật \(AB = a,\,BC = 2a\) , \(SA\) vuông góc với đáy và \(SC\) tạo với mặt phẳng \((SAB)\) một góc bằng \({60^0}\). Tính thể tích \(V\) của khối chóp đã cho.
A. \(V = \dfrac{{\sqrt 6 {a^3}}}{3}\) .
B. \(V = \sqrt 2 {a^3}\).
C.\(V = \dfrac{{\sqrt 2 {a^3}}}{3}\) .
D. \(V = \dfrac{{2{a^3}\sqrt 3 }}{9}\).
6. . Cho tứ diện \(ABCD\) có tam giác \(BCD\) vuông tại \(B,AC\) vuông góc với mặt phẳng\(\left( {BCD} \right)\), \(AC = 5a,BC = 3a\) và\(BD = 4a\). Tính bán kính \(R\) của mặt cầu ngoại tiếp tứ diện\(ABCD\).
A. \(R = \dfrac{{5a\sqrt 3 }}{2}\).
B. \(R = \dfrac{{5a\sqrt 2 }}{3}\).
C. \(R = \dfrac{{5a\sqrt 3 }}{3}\).
D. \(R = \dfrac{{5a\sqrt 2 }}{2}\).
7. . Đồ thị hàm số \(y = {x^3} + 3{x^2} – 9x – 1\) có hai cực trị \(A\) và \(B\). Điểm nào dưới đây thuộc đường thẳng\(AB\)?
A. \(N\left( {0;\,2} \right)\).
B. \(P\left( { – 1;\,1} \right)\).
C. \(Q\left( { – 1;\, – 8} \right)\).
D. \(M\left( {0;\, – 1} \right)\).
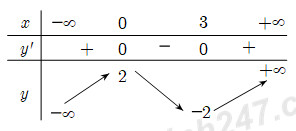
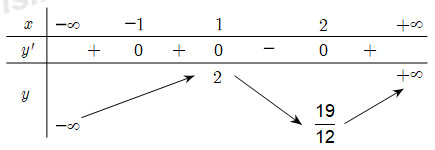
8. . Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình bên. Tìm giá trị cực đại và giá trị cực tiểu của hàm số đã cho
A. \({y_{CD}} = 3\) và \({y_{CT}} = 0\).
B. \({y_{CD}} = 2\) và \({y_{CT}} = – 2\).
C. \({y_{CD}} = – 2\) và \({y_{CT}} = 2\).
D. \({y_{CD}} = 0\) và \({y_{CT}} = 3\)
9. . Cho hình chóp \(S.ABC\) có \(AB = 6,{\rm{ }}BC = 8,{\rm{ }}AC = 10\). Cạnh bên \(SA\) vuông góc với đáy và \(SA = 4\). Tính thể tích \(V\) của khối chóp \(S.ABC\).
A. \(V = 40\).
B. \(V = 32\).
C. \(V = 192\).
D. \(V = 24\).
1.0 . Cho \(a\) là số thực dương khác 1. Mệnh đề nào dưới đây đúng với mọi số thực dương \(x,y\)?
A. \({\log _a}\left( {xy} \right) = {\log _a}x.{\log _a}y\).
B. \({\log _a}\left( {xy} \right) = {\log _a}x – {\log _a}y\)
C. \({\log _a}\left( {xy} \right) = \dfrac{{{{\log }_a}x}}{{{{\log }_a}y}}\).
D. \({\log _a}\left( {xy} \right) = {\log _a}x + {\log _a}y\).
1.1 . Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\), bảng biến thiên như sau. Kết luận nào sau đây đúng.
A. Hàm số có ba điểm cực trị.
B. Hàm số có hai điểm cực trị.
C. hàm số đạt cực tiểu tại \(x = 1\).
D. Hàm số đạt cực đại tại \(x = 2\).
1.2 . Cho \(\left( S \right)\) là một mặt cầu cố định có bán kính \(R\). Một hình trụ \(\left( H \right)\) thay đổi nhưng luôn có hai đường tròn đáy nằm trên \(\left( S \right)\). Gọi \({V_1}\) là thể tích của khối cầu \(\left( S \right)\) và \({V_2}\) là thể tích lớn nhất của khối trụ \(\left( H \right)\). Tính tỉ số \(\dfrac{{{V_1}}}{{{V_2}}}\).
A. \(\dfrac{{{V_1}}}{{{V_2}}} = \sqrt 6 \).
B. \(\dfrac{{{V_1}}}{{{V_2}}} = 2\).
C. \(\dfrac{{{V_1}}}{{{V_2}}} = \sqrt 3 \).
D. \(\dfrac{{{V_1}}}{{{V_2}}} = \sqrt 2 \)
1.3 . Cho hình nón tròn xoay có đường sinh bằng \(13\) (cm), bán kính đường tròn đáy bằng \(5\) (cm). Thể tích của khối nón tròn xoay là
A. \(200\pi \)(\({\rm{c}}{{\rm{m}}^{\rm{3}}}\)).
B. \(150\pi \)(\({\rm{c}}{{\rm{m}}^{\rm{3}}}\)).
C. \(100\pi \)(\({\rm{c}}{{\rm{m}}^{\rm{3}}}\)).
D. \(300\pi \)(\({\rm{c}}{{\rm{m}}^{\rm{3}}}\)).
1.4 . Cho hàm số \(y = \left( {x + 1} \right)\left( {{x^2} – 2} \right)\) có đồ thị \(\left( C \right)\). Mệnh đề nào dưới đây đúng?
A. \(\left( C \right)\)không cắt trục hoành.
B. \(\left( C \right)\) cắt trục hoành tại một điểm.
C. \(\left( C \right)\)cắt trục hoành tại ba điểm.
D. \(\left( C \right)\)cắt trục hoành tại hai điểm.
1.5 . Thể tích \(V\) của một khối lăng trụ có diện tích đáy bằng \(B\) và chiều cao bằng \(h\) là
A. \(V = \dfrac{1}{3}{B^2}h\).
B. \(V = Bh\).
C. \(V = \dfrac{1}{3}Bh\).
D. \(V = \dfrac{1}{2}Bh\).
1.6 . Phương trình \({2^{3 – 4x}} = \dfrac{1}{{32}}\) có nghiệm là
A. \(x = – 3\).
B. \(x = – 2\).
Advertisements (Quảng cáo)
C. \(x = 2\).
D. \(x = 3\)
1.7 . Tập xác định của hàm số \(y = {\log _2}\left( {10 – 2x} \right)\) là
A. \(\left( { – \infty ;2} \right)\).
B. \(\left( {5; + \infty } \right)\).
C. \(\left( { – \infty ;10} \right)\).
D. \(\left( { – \infty ;5} \right)\)
1.8 . Gọi \(S\) là tổng tất cả các giá trị nguyên dương của tham số \(m\) sao cho hàm số \(y = \dfrac{{2x – {m^2}}}{{x – m – 4}}\) đồng biến trên khoảng \(\left( {2021; + \infty } \right)\). Khi đó, giá trị của \(S\) bằng
A. \(2035144\).
B. \(2035145\).
C. \(2035146\).
D. \(2035143\)
1.9 . Cho hàm số \(y = {x^4} – 2{x^2}\). Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng \(\left( { – 1;1} \right)\).
B. Hàm số nghịch biến trên khoảng \(\left( { – \infty ; – 2} \right)\).
C. Hàm số đồng biến trên khoảng \(\left( { – 1;1} \right)\).
D. Hàm số đồng biến trên khoảng \(\left( { – \infty ; – 2} \right)\)
2.0 . Cho mặt cầu \(\left( S \right)\) có tâm \(O\), bán kính \(r\). Mặt phẳng \(\left( \alpha \right)\) cắt mặt cầu \(\left( S \right)\) theo giao tuyến là đường tròn \(\left( C \right)\) có bán kính \(R\). Kết luận nào sau đây sai?
A. \(R = \sqrt {{r^2} + {d^2}\left( {O,\left( \alpha \right)} \right)} \).
B. \(d\left( {O,\left( \alpha \right)} \right) < r\).
C. Diện tích của mặt cầu là \(S = 4\pi {r^2}\).
D. Đường tròn lớn của mặt cầu có bán kính bằng bán kính mặt cầu
2.1 . Với \(a,\,b,\,x\) là các số thực dương thỏa mãn \({\log _5}x = 4{\log _5}a + 3{\log _5}b\), mệnh đề nào dưới đây là đúng?
A. \(x = 3a + 4b\).
B. \(x = 4a + 3b\).
C. \(x = {a^4}{b^3}\).
D. \(x = {a^4} + {b^3}\).
2.2 . Một khối trụ có khoảng cách giữa hai đáy, độ dài đường sinh và bán kính đường tròn đáy lần lượt bằng \(h,\,{\rm{ }}l,\,{\rm{ }}r\). Khi đó công thức tính diện tích toàn phần của khối trụ là
A. \({S_{tp}} = 2\pi r\left( {l + r} \right)\).
B. \({S_{tp}} = 2\pi r\left( {l + 2r} \right)\).
C. \({S_{tp}} = \pi r\left( {l + r} \right)\).
D. \({S_{tp}} = \pi r\left( {2l + r} \right)\).
2.3 . Cho hình nón tròn xoay. Một mặt phẳng \(\left( P \right)\) đi qua đỉnh \(O\) của hình nón và cắt đường tròn đáy của hình nón tại hai điểm. Thiết diện được tạo thành là
A. Một tứ giác.
B. Một hình thang cân.
C. Một ngũ giác.
D. Một tam giác cân.
2.4 . Cho \({\pi ^\alpha } > {\pi ^\beta }\) với \(\alpha ,\,\beta \in \mathbb{R}\). Mện đề nào dưới đây là đúng?
A. \(\alpha > \beta \).
B. \(\alpha < \beta \).
C. \(\alpha = \beta \).
D. \(\alpha \le \beta \).
2.5 . Khối đa diện nào sau đây có công thức thể tích là \(V = \dfrac{1}{3}Bh\)? Biết hình đa diện đó có diện tích đáy bằng \(B\) và chiều cao bằng \(h\)?
A. Khối chóp.
B. Khối hộp chữ nhật.
C. Khối hộp.
D. Khối lăng trụ.
2.6 . Đồ thị \(y = \dfrac{{x – 2}}{{\sqrt {{x^2} – 4} }}\) có bao nhiêu tiệm cận?
A. 2.
B. 4.
C. 3.
Advertisements (Quảng cáo)
D. 1.
2.7 . Cho 4 số thực a, b, x, y với \(a,{\rm{ }}b\) là các số dương và khác 1. Mệnh đề nào dưới đây đúng?
A. \(\dfrac{{{a^x}}}{{{a^y}}} = {a^{x – y}}\).
B. \({\left( {{a^x}} \right)^y} = {a^{x + y}}\).
C. \({a^x}.{a^y} = {a^{x.y}}\)
D. \({\left( {a.b} \right)^x} = a.{b^x}\).
2.8 . Hai thành phố A và B ngăn cách nhau bởi một còn sông. Người ta cần xây cây cầu bắc qua sông và vuông góc với bờ sông. Biết rằng thành phố A cách bờ sông 2 (km), thành phố B cách bờ sông 5 (km), khoảng cách giữa đường thẳng đi qua A và đường thẳng đi qua B cùng vuông góc với bờ sông là 12 (km). Giả sử hai bờ sông là hai đường thẳng song song với nhau. Nhằm tiết kiệm chi phí đi từ thành phố A đến thành phố B, người ta xây cây cầu ở vị trí MN để quãng đường đi từ thành phố A đến thành phố B là ngắn nhất (hình vẽ). Khi đó, độ dài đoạn AM là
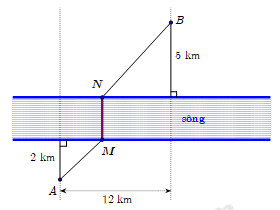
A. \(AM = \dfrac{{2\sqrt {193} }}{7}\;{\rm{km}}{\rm{.}}\).
B. \(AM = \dfrac{{3\sqrt {193} }}{7}\;{\rm{km}}{\rm{.}}\)
C. \(AM = \sqrt {193} \;{\rm{km}}{\rm{.}}\)
D. \(AM = \dfrac{{\sqrt {193} }}{7}\;{\rm{km}}{\rm{.}}\)
2.9 . Đạo hàm của hàm số \(y = {5^x} + 2017\) là
A. \(y’ = \dfrac{{{5^x}}}{{5\ln 5}}\).
B. \(y’ = {5^x}.\ln 5\).
C. \(y’ = \dfrac{{{5^x}}}{{\ln 5}}\)
D. \(y’ = {5^x}\).
3.0 . Cho khối chóp \(S.ABCD\) có đáy là hình vuông, \(\Delta {\rm{ }}SAB\) đều và nằm trong mặt phẳng vuông góc với mặt đáy. Mặt cầu ngoại tiếp khối chóp \(S.ABCD\) có diện tích \(84\pi {\rm{ c}}{{\rm{m}}^{\rm{2}}}\). Khoảng cách giữa hai đường thẳng \(SA\) và \(BD\) là
A. \(\dfrac{{3\sqrt {21} }}{7}\;{\rm{cm}}\).
B. \(\dfrac{{2\sqrt {21} }}{7}\;{\rm{cm}}\).
C. \(\dfrac{{\sqrt {21} }}{7}\;{\rm{cm}}\).
D. \(\dfrac{{6\sqrt {21} }}{7}\;{\rm{cm}}\).
3.1 . Tìm tập xác định \(D\) của hàm số \(y = {\left( {{x^2} + x – 2} \right)^{ – 3}}\).
A. \(D = \left( {0; + \infty } \right)\).
B. \(D = \left( { – \infty ; – 2} \right) \cup \left( {1; + \infty } \right)\).
C. \(D = \mathbb{R}\backslash \left\{ { – 2;1} \right\}\).
D. \(D = \mathbb{R}\).
3.2 . Tìm các giá trị của tham số \(m\) để hàm số \(y = \dfrac{{{x^3}}}{3} – 3{x^2} + {m^2}x + 2m – 3\) đồng biến trên \(\mathbb{R}\).
A. \(\left[ \begin{array}{l}m < – 3\\m > 3\end{array} \right.\).
B. \( – 3 \le m \le 3\).
C. \( – 3 < m < 3\).
D. \(\left[ \begin{array}{l}m \le – 3\\m \ge 3\end{array} \right.\).
3.3 . Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A. Với \(0 < a < 1\), hàm số \(y = {\log _a}x\) là một hàm nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).
B. Với \(a > 1\), hàm số \(y = {\log _a}x\) là một hàm đồng biến trên khoảng \(\left( { – \infty ; + \infty } \right)\).
C. Với \(a > 1\), hàm số \(y = {a^x}\) là một hàm đồng biến trên khoảng \(\left( { – \infty ; + \infty } \right)\).
D. Với \(0 < a < 1\), hàm số \(y = {a^x}\) là một hàm nghịch biến trên khoảng \(\left( { – \infty ; + \infty } \right)\).
3.4 . Xét các số thực dương \(x,y\) thỏa mãn \({\log _3}\dfrac{{1 – y}}{{x + 3xy}} = 3xy + x + 3y – 4\). Tìm giá trị nhỏ nhất \({P_{\min }}\) của \(P = x + y\).
A. \({P_{\min }} = \dfrac{{4\sqrt 3 + 4}}{3}\).
B. \({P_{\min }} = \dfrac{{4\sqrt 3 – 4}}{3}\).
C. \({P_{\min }} = \dfrac{{4\sqrt 3 – 4}}{9}\).
D. \({P_{\min }} = \dfrac{{4\sqrt 3 + 4}}{9}\).
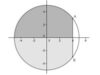
3.5 . Hình vẽ sau đây là đồ thị của hàm số nào ?
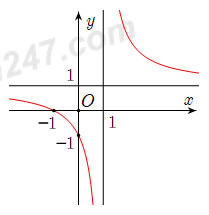
A. \(y = \dfrac{{x + 2}}{{x + 1}}\).
B. \(y = \dfrac{{x + 3}}{{1 – x}}\).
C. \(y = \dfrac{{2x + 1}}{{2x – 1}}\).
D. \(y = \dfrac{{x + 1}}{{x – 1}}\).
36 . Tính đạo hàm của hàm số \(y = \log \left( {2{\rm{x}} + 1} \right)\).
A. \(y’ = \dfrac{2}{{\left( {2{\rm{x}} + 1} \right)\ln 10}}\).
B. \(y’ = \dfrac{2}{{\left( {2{\rm{x}} + 1} \right)}}\).
C. \(y’ = \dfrac{1}{{\left( {2{\rm{x}} + 1} \right)\ln 10}}\).
D. \(y’ = \dfrac{1}{{\left( {2{\rm{x}} + 1} \right)}}\).
37 . Mỗi cạnh của một hình đa diện là cạnh chung của đúng \(n\) mặt của hình đa diện đó. Mệnh đề nào dưới đây đúng?
A. \(n = 2\).
B. \(n = 5\).
C. \(n = 3\).
D. \(n = 4\).
3.8 . Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu đạo hàm như sau

Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng \(\left( { – \infty ;2} \right)\).
B. Hàm số nghịch biến trên khoảng \(\left( { – \infty ; – 2} \right)\).
C. Hàm số nghịch biến trên khoảng \(\left( { – \infty ;0} \right)\).
D. Hàm số nghịch biến trên khoảng \(\left( { – 2;0} \right)\).
39 . Hình vẽ sau đây là đồ thị của hàm số nào?
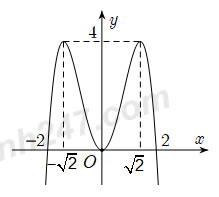
A. \(y = – {x^4} – 2{x^2}\)
B. \(y = – {x^4} + 3{x^2} + 1\)
C. \(y = – {x^4} + 4{x^2}\)
D. \(y = {x^4} – 3{x^2}\)
4.0 . Cho hàm số \(f\left( x \right) = \dfrac{{x – {m^2}}}{{x + 8}},\) với \(m\) là tham số. Giá trị lớn nhất của \(m\) để \(\mathop {\min }\limits_{\left[ {0;3} \right]} f\left( x \right) = – 2\) là
A. \(m = 5\).
B. \(m = 6\).
C. \(m = 4\).
D. \(m = 3\).
4.1 . Tìm giá trị thực của tham số \(m\) để phương trình \({9^x} – {2.3^{x + 1}} + m = 0\) có hai nghiệm thực \({x_1},{x_2}\) thỏa mãn \({x_1} + {x_2} = 0\).
A. \(m = 6\).
B. \(m = 0\).
C. \(m = 3\).
D. \(m = 1\).
4.2 . Giá trị lớn nhất của hàm số \(y = \dfrac{{x + 4}}{{x – 2}}\) trên đoạn \(\left[ {3,4} \right]\).
A. \( – 4\).
B. \(10\).
C. \(7\).
D. \(8\).
4.3 . Tìm giá trị thực của tham số \(m\) để hàm số \(y = \dfrac{1}{3}{x^3} – m{x^2} + \left( {{m^2} – 4} \right)x + 3\) đạt cực tiểu tại \(x = 3\).
A. \(m = 1\).
B. \(m = – 1\).
C. \(m = 5\).
D. \(m = – 7\).
4.4 . Cho khối lăng trụ đứng \(ABC.A’B’C’\) có đáy là tam giác cân \(ABC\) với \(AB = AC = a\), \(\widehat {BAC} = 120^\circ \), mặt phẳng \(\left( {AB’C’} \right)\) tạo với đáy một góc \(30^\circ \). Tính thể tích \(V\) của khối lăng trụ đã cho.
A. \(V = \dfrac{{{a^3}}}{6}\).
B. \(V = \dfrac{{{a^3}}}{8}\).
C. \(V = \dfrac{{3{a^3}}}{8}\).
D. \(V = \dfrac{{9{a^3}}}{8}\).
4.5 . Cho khối lăng trụ đứng \(ABC.A’B’C’\) có \(AA’ = a\), đáy \(ABC\) là tam giác vuông cân tại \(A\) và \(BC = a\sqrt 2 \). Tính thể tích \(V\) của khối lăng trụ đã cho.
A. \(V = {a^3}\).
B. \(V = \dfrac{{{a^3}}}{2}\).
C. \(V = \dfrac{{{a^3}}}{6}\).
D. \(V = \dfrac{{{a^3}}}{3}\).
4.6 . Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật \(ABCD\) có \(AB\) và \(CD\) thuộc hái đáy của hình trụ, \(AB = 4a,\,AC = 5a\). Thể tích của khối trụ.
A. \(8\pi {a^3}\).
B. \(12\pi {a^3}\).
C. \(4\pi {a^3}\).
D. \(16\pi {a^3}\).
4.7 . Cho hình nón tròn xoay có bán kính đường tròn đáy \(r\), chiều cao \(h\) và đường sinh \(l\). Kết luận nào sau đây sai?
A. \(V = \dfrac{1}{3}\pi {r^2}h\).
B. \({S_{tp}} = \pi rl + \pi {r^2}\).
C. \({h^2} = {r^2} + {l^2}\).
D. \({S_{xq}} = \pi rl\).
4.8 . Hàm số \(y = f\left( x \right)\) có giới hạn \(\mathop {\lim }\limits_{x \to {a^ – }} f\left( x \right) = + \infty \) và đồ thị \(\left( C \right)\) của hàm số \(y = f\left( x \right)\) chỉ nhận đường thẳng \(d\) làm tiệm cận đứng. Khẳng định nào sau đây đúng?
A. \(d:y = a\).
B. \(d:x = a\).
C. \(d:x = – a\).
D. \(d:y = – a\).
4.9 . Rút gọn biểu thức \(M = \dfrac{{{a^{\dfrac{1}{5}}}\left( {{a^{\dfrac{3}{{10}}}} – {a^{ – \dfrac{1}{5}}}} \right)}}{{{a^{\dfrac{2}{3}}}\left( {{a^{\dfrac{1}{3}}} – {a^{ – \dfrac{2}{3}}}} \right)}}\) với \(a > 0,\,a \ne 1\), ta được kết quả là
A. \(\dfrac{1}{{\sqrt a + 1}}\).
B. \(\dfrac{1}{{a + 1}}\).
C. \(\dfrac{1}{{a – 1}}\).
D. \(\dfrac{1}{{\sqrt a – 1}}\).
5.0 . Đầu mỗi tháng anh A gửi vào ngân hàng 3 triệu đồng với lãi suất kép là \(0,6\% \) mỗi tháng. Hỏi sau ít nhất bao nhiêu tháng (khi ngân hàng đã tính lãi) thì anh A có được số tiền cả lãi và gốc nhiều hơn 100 triệu biết lãi suất không đổi trong quá trình gửi.
A. 31 tháng.
B. 40 tháng.
C. 35 tháng.
D. 30 tháng.

| 1. D | 2. C | 3. A | 4. C | 5. D |
| 6. D | 7. A | 8. B | 9. B | 10. D |
| 11. B | 12. C | 13. C | 14. C | 15. B |
| 16. C | 17. D | 18. D | 19. B | 20. A |
| 21. C | 22. A | 23. A | 24. A | 25. A |
| 26. C | 27. A | 28. A | 29. B | 30. D |
| 31. C | 32. D | 33. B | 34. B | 35. D |
| 36. A | 37. A | 38. D | 39. C | 40. C |
| 41. D | 42. C | 43. A | 44. B | 45. B |
| 46. B | 47. C | 48. B | 49. A | 50. A |