
1. Trong không gian với hệ trục tọa độ \(Oxyz\), gọi \((P)\)là mặt phẳng song song với mặt phẳng \(Oxz\) và cắt mặt cầu \({(x – 1)^2} + {(y + 2)^2} + {z^2} = 12\)theo đường tròn có chu vi lớn nhất. Phương trình của \((P)\) là:
A.\(x – 2y + 1 = 0\). B.\(y – 2 = 0\).
C.\(y + 1 = 0\). D.\(y + 2 = 0\).
2. Trong không gian với hệ trục tọa độ \(Oxyz\), cho điểm \(M(1;2;3).\) Gọi \((\alpha )\) là mặt phẳng chứa trục \(Oy\) và cách \(M\) một khoảng lớn nhất. Phương trình của \((\alpha )\) là:
A.\(x + 3z = 0\). B.\(x + 2z = 0\).
C. \(x – 3z = 0\). D.\(x = 0\).
3. Trong không gian với hệ trục toạ độ \(Oxyz\), cho mặt cầu \(\left( S \right):{\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} + {\left( {z – 3} \right)^2} = 9\), điểm \(A\left( {0;0;2} \right)\). Phương trình mặt phẳng \(\left( P \right)\) đi qua \(A\) và cắt mặt cầu \(\left( S \right)\) theo thiết diện là hình tròn \(\left( C \right)\)có diện tích nhỏ nhất ?
A.\(\left( P \right):x + 2y + 3z – 6 = 0\).
B. \(\left( P \right):x + 2y + z – 2 = 0\).
C.\(\left( P \right):3x + 2y + 2z – 4 = 0\).
D. \(\left( P \right):x – 2y + 3z – 6 = 0\).
4. Trong không gian với hệ toạ độ \(Oxyz\), cho điểm \(N\left( {1;1;1} \right)\). Viết phương trình mặt phẳng \(\left( P \right)\) cắt các trục \(Ox,Oy,Oz\) lần lượt tại \(A,B,C\) (không trùng với gốc tọa độ\(O\)) sao cho \(N\) là tâm đường tròn ngoại tiếp tam giác \(ABC\)
A.\(\left( P \right):x + y + z – 3 = 0\).
B.\(\left( P \right):x + y – z + 1 = 0\).
C.\(\left( P \right):x – y – z + 1 = 0\).
D.\(\left( P \right):x + 2y + z – 4 = 0\).
5. Trong không gian với hệ toạ độ \(Oxyz\), viết phương trình mặt phẳng \(\left( P \right)\) đi qua hai điểm \(A(1;1;1)\), \(B\left( {0;2;2} \right)\) đồng thời cắt các tia \(Ox,Oy\) lần lượt tại hai điểm \(M,N\) (không trùng với gốc tọa độ\(O\)) sao cho \(OM = 2ON\)
A.\(\left( P \right):2x + 3y – z – 4 = 0\).
B.\(\left( P \right):x + 2y – z – 2 = 0\).
C.\(\left( P \right):x – 2y – z + 2 = 0\).
D.\(\left( P \right):3x + y + 2z – 6 = 0\).
6. Trong không gian với hệ trục tọa độ \(Oxyz\), cho tứ diện \(ABCD\) có các đỉnh \(A\left( {1;2;1} \right)\), \(B\left( { – 2;1;3} \right)\), \(C\left( {2; – 1;3} \right)\) và \(D\left( {0;3;1} \right)\). Phương trình mặt phẳng \(\left( \alpha \right)\) đi qua \(A,B\) đồng thời cách đều \(C,D\)
A.\(\left( {{P_1}} \right):4x + 2y + 7z – 15 = 0;\)\(\,\left( {{P_2}} \right):x – 5y – z + 10 = 0\).
B.\(\left( {{P_1}} \right):6x – 4y + 7z – 5 = 0;\)\(\,\left( {{P_2}} \right):3x + y + 5z + 10 = 0\).
C.\(\left( {{P_1}} \right):6x – 4y + 7z – 5 = 0;\)\(\,\left( {{P_2}} \right):2x + 3z – 5 = 0\).
D. \(\left( {{P_1}} \right):3x + 5y + 7z – 20 = 0;\)\(\,\left( {{P_2}} \right):x + 3y + 3z – 10 = 0\).
7. Cho các điểm \(I\left( {1;1; – 2} \right)\) và đường thẳng \(d:\left\{ \begin{array}{l}x = – 1 + t\\y = 3 + 2t\\z = 2 + t\end{array} \right.\). Phương trình mặt cầu \(\left( S \right)\)có tâm I và cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB vuông là:
A.\({\left( {x – 1} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z + 2} \right)^2} = 3.\)
B. \({\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z – 2} \right)^2} = 9.\)
C. \({\left( {x – 1} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z + 2} \right)^2} = 9.\)
D.\({\left( {x – 1} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z + 2} \right)^2} = 36.\)
8. Cho điểm \(I\left( {1;1; – 2} \right)\) đường thẳng \(d:\dfrac{{x + 1}}{1} = \dfrac{{y – 3}}{2} = \dfrac{{z – 2}}{1}.\) Phương trình mặt cầu \(\left( S \right)\)có tâm I và cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB đều là:
A.\({\left( {x – 1} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z + 2} \right)^2} = 24.\)
B. \({\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z – 2} \right)^2} = 24.\)
C. \({\left( {x – 1} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z + 2} \right)^2} = 18\)
D.\({\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z – 2} \right)^2} = 18.\)
9. Cho điểm \(I\left( {1;1; – 2} \right)\) đường thẳng \(d:\dfrac{{x + 1}}{1} = \dfrac{{y – 3}}{2} = \dfrac{{z – 2}}{1}\). Phương trình mặt cầu \(\left( S \right)\)có tâm I và cắt đường thẳng d tại hai điểm A, B sao cho \(\widehat {IAB} = {30^o}\) là:
A.\({\left( {x – 1} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z + 2} \right)^2} = 72.\)
B. \({\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z – 2} \right)^2} = 36.\)
C. \({\left( {x – 1} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z + 2} \right)^2} = 66.\)
D.\({\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z – 2} \right)^2} = 46.\)
10: Phương trình mặt cầu có tâm \(I\left( {3;\sqrt 3 ; – 7} \right)\) và tiếp xúc trục tung là:
A. \({\left( {x – 3} \right)^2} + {\left( {y – \sqrt 3 } \right)^2} + {\left( {z + 7} \right)^2} = 61.\)
B.\({\left( {x – 3} \right)^2} + {\left( {y – \sqrt 3 } \right)^2} + {\left( {z + 7} \right)^2} = 58.\)
C. \({\left( {x + 3} \right)^2} + {\left( {y + \sqrt 3 } \right)^2} + {\left( {z – 7} \right)^2} = 58.\)
D.\({\left( {x – 3} \right)^2} + {\left( {y – \sqrt 3 } \right)^2} + {\left( {z + 7} \right)^2} = 12.\)
11: Phương trình mặt cầu có tâm \(I\left( {\sqrt 5 ;3;9} \right)\) và tiếp xúc trục hoành là:
A. \({\left( {x + \sqrt 5 } \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z + 9} \right)^2} = 86.\)
B. \({\left( {x – \sqrt 5 } \right)^2} + {\left( {y – 3} \right)^2} + {\left( {z – 9} \right)^2} = 14.\)
C. \({\left( {x – \sqrt 5 } \right)^2} + {\left( {y – 3} \right)^2} + {\left( {z – 9} \right)^2} = 90.\)
D. \({\left( {x + \sqrt 5 } \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z + 9} \right)^2} = 90.\)
12: Ba đỉnh của một hình bình hành có tọa độ là\(\left( {1;1;1} \right),\,\left( {2;3;4} \right),\,\left( {7;7;5} \right)\). Diện tích của hình bình hành đó bằng
A. \(2\sqrt {83} \). B. \(\sqrt {83} \).
C. \(83\). D. \(\dfrac{{\sqrt {83} }}{2}\).
13: Cho 3 vecto \(\overrightarrow a = \left( {1;2;1} \right);\)\(\overrightarrow b = \left( { – 1;1;2} \right)\) và \(\overrightarrow c = \left( {x;3x;x + 2} \right)\) . Tìm \(x\) để 3 vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng
A.\(2.\) B.\( – 1.\)
C. \( – 2.\) D. \(1.\)
14: Trong không gian tọa độ \(Oxyz\)cho ba điểm \(A\left( {2;5;1} \right),\,B\left( { – 2; – 6;2} \right),\,C\left( {1;2; – 1} \right)\) và điểm \(M\left( {m;m;m} \right)\), để \(M{A^2} – M{B^2} – M{C^2}\) đạt giá trị lớn nhất thì \(m\) bằng
Advertisements (Quảng cáo)
A. 3. B. 4.
C. 2. D. 1.
15: Cho hình chóp \(S.ABCD\)biết \(A\left( { – 2;2;6} \right),\,B\left( { – 3;1;8} \right),\)\(\,C\left( { – 1;0;7} \right),\,D\left( {1;2;3} \right)\). Gọi \(H\) là trung điểm của \(CD,\) \(SH \bot \left( {ABCD} \right)\). Để khối chóp \(S.ABCD\)có thể tích bằng \(\dfrac{{27}}{2}\) (đvtt) thì có hai điểm \({S_1},\,{S_2}\) thỏa mãn yêu cầu bài toán. Tìm tọa độ trung điểm \(I\) của \({S_1}{S_2}\)
A. \(I\left( {0; – 1; – 3} \right)\). B. \(I\left( {1;0;3} \right)\)
C.\(I\left( {0;1;3} \right)\). D. \(I\left( { – 1;0; – 3} \right).\)
16: Trong không gian \(Oxyz\), cho hai điểm \(A(2; – 1;7),B(4;5; – 2)\). Đường thẳng \(AB\)cắt mặt phẳng \((Oyz)\) tại điểm \(M\). Điểm \(M\)chia đoạn thẳng \(AB\) theo tỉ số nào
A. \(\dfrac{1}{2}\). B. \(2\).
C. \(\dfrac{1}{3}\). D. \(\dfrac{2}{3}\).
17: Trong không gian \(Oxyz\), cho tứ diện \(ABCD\) có \(A(2;1; – 1),B(3;0;1),C(2; – 1;3)\) và \(D\) thuộc trục \(Oy\). Biết \({V_{ABCD}} = 5\) và có hai điểm \({D_1}\left( {0;{y_1};0} \right),\,{D_2}\left( {0;{y_2};0} \right)\) thỏa mãn yêu cầu bài toán. Khi đó \({y_1} + {y_2}\) bằng
A. \(0.\) B. \(1\).
C. \(2\). D. \(3\).
18: Trong không gian \(BD\), cho mặt cầu \(\overrightarrow {A’X} = \left( {\dfrac{a}{2};\dfrac{a}{2}; – b} \right)\); và mặt phẳng \(\overrightarrow {MX} = \left( { – \dfrac{a}{2}; – \dfrac{a}{2}; – \dfrac{b}{2}} \right)\).
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Mặt cầu \( \Rightarrow – {\left( {\dfrac{a}{2}} \right)^2} – {\left( {\dfrac{a}{2}} \right)^2} + \dfrac{{{b^2}}}{2} = 0\) có tâm \( \Rightarrow \dfrac{a}{b} = 1\) bán kính \(Oxyz\).
B. \(\left( {A’BD} \right) \bot \left( {MBD} \right) \Rightarrow A’X \bot MX\)cắt \( \Rightarrow \overrightarrow {A’X} .\overrightarrow {MX} = 0\) theo giao tuyến là đường tròn.
C. Mặt phẳng \((P):\;x + 2y + 2z + 4 = 0\) không cắt mặt cầu \((S):{x^2} + {y^2} + {z^2} – 2x – 2y – 2z – 1 = 0.\).
D. Khoảng cách từ tâm của \(M\) đến \(\left( S \right)\) bằng \(d\left( {M,\left( P \right)} \right)\).
19: Trong không gian \(B\left( {\dfrac{1}{3}; – \dfrac{1}{3}; – \dfrac{1}{3}} \right)\), cho mặt cầu \(d(A,(P)) = 5 \ge d(B,(P)) = 1.\) có tâm \( \Rightarrow d(A,(P)) \ge d(M,(P)) \ge d(B,(P)).\) tiếp xúc với mặt phẳng \( \Rightarrow d{(M,(P))_{\min }} = 1 \Leftrightarrow M \equiv B.\). Mặt cầu \(Oxyz\) có bán kính \(2x – 2y – z + 9 = 0\) bằng:
A.\(M\). B.\((S):{(x – 3)^2} + {(y + 2)^2} + {(z – 1)^2} = 100\).
C.\((S)\). D.\(M\).
20: Trong không gian \(M\left( { – \dfrac{{29}}{3};\dfrac{{26}}{3}; – \dfrac{7}{3}} \right)\), cho mặt phẳng \(M\left( {\dfrac{{11}}{3};\dfrac{{14}}{3}; – \dfrac{{13}}{3}} \right)\) : \((S)\)và điểm \(I(3; – 2;1)\). Phương trình mặt cầu tâm \(I\)và tiếp xúc với mặt phẳng \((P)\) là:
A.\(d(I;(P)) = 6 < R\).
B.\((P)\).
C.\((S)\).

|
Câu |
1 |
2 |
3 |
4 |
5 |
|
Đáp án |
D |
A |
B |
A |
C |
|
Câu |
6 |
7 |
8 |
9 |
10 |
|
Đáp án |
D |
D |
A |
A |
B |
|
Câu |
11 |
12 |
13 |
14 |
15 |
|
Đáp án |
C |
A |
A |
B |
C |
|
Câu |
16 |
17 |
18 |
19 |
20 |
|
Đáp án |
A |
A |
B |
B |
A |
Lời giải chi tiết:
1. Phương pháp tự luận
Mặt phẳng \((P)\) cắt mặt cầu \({(x – 1)^2} + {(y + 2)^2} + {z^2} = 12\) theo đường tròn có chu vi lớn nhất nên mặt phẳng \((P)\) đi qua tâm \(I(1; – 2;0)\).
Phương trình mặt phẳng \((P)\) song song với mặt phẳng \(Oxz\) có dạng :\(Ay + B = 0\)
Do \((P)\) đi qua tâm \(I(1; – 2;0)\)có phương trình dạng: \(y + 2 = 0\).
Phương pháp trắc nghiệm
+) Mặt phẳng \((P)\) song song với mặt phẳng \(Oxz\) nên lọai đáp án D.
+) Mặt phẳng \((P)\)đi qua tâm \(I(1; – 2;0)\)nên thay tọa độ điểm \(I\)vào các phương trình loại được đáp án B,C.
2. Phương pháp tự luận:
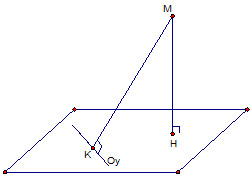
+) Gọi \(H,K\)lần lượt là hình chiếu vuông góc của \(M\)trên mặt phẳng\((\alpha )\) và trục \(Oy\).
Ta có : \(K(0;2;0)\)
\(d(M,(\alpha )) = MH \le MK\)
Advertisements (Quảng cáo)
Vậy khoảng cách từ \(M\) đến mặt phẳng\((\alpha )\) lớn nhất khi mặt phẳng\((\alpha )\)qua \(K\) và vuông góc với\(MK\).
Phương trình mặt phẳng: \(x + 3z = 0\)
3. Mặt cầu \(\left( S \right)\) có tâm \(I\left( {1,2,3} \right),R = 3\).
Ta có \(IA < R\) nên điểm \(A\)nằm trong mặt cầu.
Ta có : \(d\left( {I,\left( P \right)} \right) = \sqrt {{R^2} – {r^2}} \)
Diện tích hình tròn \(\left( C \right)\) nhỏ nhất \( \Leftrightarrow \)\(r\)nhỏ nhất \( \Leftrightarrow d\left( {I,\left( P \right)} \right)\) lớn nhất.
Do \(d\left( {I,\left( P \right)} \right) \le IA\)\( \Rightarrow \max d\left( {I,\left( P \right)} \right) = IA\) Khi đó mặt phẳng\(\left( P \right)\) đi qua \(A\) và nhận \(\overrightarrow {IA} \) làm vtpt
\( \Rightarrow \left( P \right):x + 2y + z – 2 = 0\)
4. Gọi \(A\left( {a;0;0} \right),B\left( {0;b;0} \right),C\left( {0;0;c} \right)\) lần lượt là giao điểm của \(\left( P \right)\) với các trục \(Ox,Oy,Oz\)
\( \Rightarrow \)\(\left( P \right):\dfrac{x}{a} + \dfrac{y}{b} + \dfrac{z}{c} = 1\left( {a,b,c \ne 0} \right)\)
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{N \in \left( P \right)}\\{NA = NB}\\{NA = NC}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} = 1}\\{\left| {a – 1} \right| = \left| {b – 1} \right|}\\{\left| {a – 1} \right| = \left| {c – 1} \right|}\end{array}} \right. \)
\(\Leftrightarrow a = b = c = 3 \Rightarrow x + y + z – 3 = 0\)
5. Gọi \(M\left( {a;0;0} \right),N\left( {0;b;0} \right)\) lần lượt là giao điểm của \(\left( P \right)\) với các tia \(Ox,Oy\)\(\left( {a,b > 0} \right)\)
Do \(OM = 2ON\)\( \Leftrightarrow a = 2b\)\( \Rightarrow \overrightarrow {MN} \left( { – 2b;b;0} \right) = – b\left( {2; – 1;0} \right)\) .Đặt \(\overrightarrow u \left( {2; – 1;0} \right)\)
Gọi \(\overrightarrow n \) là môt vectơ pháp tuyến của mặt phẳng \(\left( P \right)\)\( \Rightarrow \)\(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow {AB} } \right] = \left( { – 1;2;1} \right)\)
Phương trình măt phẳng \(\left( P \right):x – 2y – z + 2 = 0\).
6. Trường hợp 1:\(CD//\left( P \right)\)
\(\overrightarrow {{n_P}} = \left[ {\overrightarrow {AB} ,\overrightarrow {CD} } \right] = \left( { – 6; – 10; – 14} \right)\)\(\, = – 2\left( {3;5;7} \right)\)
\( \Rightarrow \left( P \right):3x + 5y + 7z – 20 = 0\)
Trường hợp 2:\(\left( P \right)\) đi qua trung điểm \(I\left( {1;1;2} \right)\) của \(CD\)
\(\overrightarrow {{n_P}} = \left[ {\overrightarrow {AB} ,\overrightarrow {AI} } \right] = \left( {1;3;3} \right) \)
\(\Rightarrow \left( P \right):x + 3y + 3z – 10 = 0\).
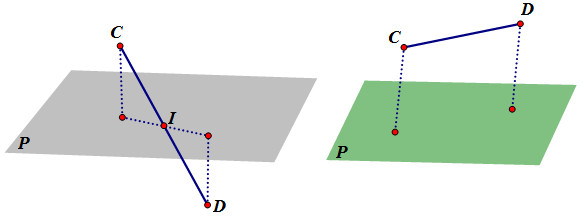
7. Đường thẳng \(d\) đi qua \(M\left( { – 1;{\rm{ 3}};2} \right)\)và có vectơ chỉ phương \(\overrightarrow u = \left( {1;\,2;\,1} \right)\).
Gọi H là hình chiếu của I trên D. Ta có : \(IH = d\left( {I;AB} \right) = \dfrac{{\left| {\left[ {\overrightarrow u ,\overrightarrow {MI} } \right]} \right|}}{{\left| {\overrightarrow u } \right|}} = \sqrt {18} \)
\( \Rightarrow {R^2} = I{H^2} + {\left( {\dfrac{{AB}}{2}} \right)^2} = 36\).
Vậy phương trình mặt cầu là: \({\left( {x – 1} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z + 2} \right)^2} = 36.\)
Lựa chọn đáp án D.
8. Đường thẳng \(d\) đi qua \(M\left( { – 1;{\rm{ 3}};2} \right)\)và có vectơ chỉ phương \(\overrightarrow u = \left( {1;\,2;\,1} \right)\).
Gọi H là hình chiếu của I trên D. Ta có : \(IH = d\left( {I;AB} \right) = \dfrac{{\left| {\left[ {\overrightarrow u ,\overrightarrow {MI} } \right]} \right|}}{{\left| {\overrightarrow u } \right|}} = \sqrt {18} \).
\( \Rightarrow IH = R.\dfrac{{\sqrt 3 }}{2} \Rightarrow R = \dfrac{{2IH}}{{\sqrt 3 }} = 2\sqrt 6 \).
Vậy phương trình mặt cầu là : \({\left( {x – 1} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z + 2} \right)^2} = 24.\)
Lựa chọn đáp án A.
9. Đường thẳng \(d\) đi qua \(M\left( { – 1;{\rm{ 3}};2} \right)\)và có vectơ chỉ phương \(\overrightarrow u = \left( {1;\,2;\,1} \right)\).
Gọi H là hình chiếu của I trên D. Ta có: \(IH = d\left( {I;AB} \right) = \dfrac{{\left| {\left[ {\overrightarrow u ,\overrightarrow {MI} } \right]} \right|}}{{\left| {\overrightarrow u } \right|}} = \sqrt {18} \).
\( \Rightarrow R = IA = 2\sqrt {18} \).
Vậy phương trình mặt cầu là: \({\left( {x – 1} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z + 2} \right)^2} = 72.\)
Lựa chọn đáp án A.
10: Gọi H là hình chiếu của \(I\left( {3;\sqrt 3 ; – 7} \right)\) trên Oy\( \Rightarrow H\left( {0;\sqrt 3 ;0} \right)\)\( \Rightarrow R = IH = \sqrt {58} \)
Vậy phương trình mặt cầu là: \({\left( {x – 3} \right)^2} + {\left( {y – \sqrt 3 } \right)^2} + {\left( {z + 7} \right)^2} = 58.\)
Lựa chọn đáp án B.
11: Gọi H là hình chiếu của \(I\left( {\sqrt 5 ;3;9} \right)\) trên Ox\( \Rightarrow H\left( {\sqrt 5 ;0;0} \right)\)\( \Rightarrow R = IH = \sqrt {90} \)
Vậy phương trình mặt cầu là: \({\left( {x – \sqrt 5 } \right)^2} + {\left( {y – 3} \right)^2} + {\left( {z – 9} \right)^2} = 90.\)
Lựa chọn đáp án C.
12:Gọi 3 đỉnh theo thứ tự là \(A,B,C\)
\(\overrightarrow {AB} = \left( {1;2;3} \right),\overrightarrow {AC} = \left( {6;6;4} \right)\)
\({S_{hbh}} = \left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]} \right| \)\(\,= \sqrt {{{\left( { – 10} \right)}^2} + {{14}^2} + {{\left( { – 6} \right)}^2}} = 2\sqrt {83} \)
13:
\(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng thì \(\left[ {\overrightarrow {\overrightarrow a ,b} } \right].\overrightarrow c = 0 \Rightarrow x = 2.\)
14: \(\overrightarrow {MA} = \left( {2 – m;5 – m;1 – m} \right),\)\(\,\overrightarrow {MB} = \left( { – 2 – m; – 6 – m;2 – m} \right),\)\(\,\overrightarrow {MC} = \left( {1 – m;2 – m; – 1 – m} \right)\)
\(M{A^2} – M{B^2} – M{C^2} \)\(\,= – 3{m^2} – 24m – 20 \)\(\,= 28 – 3{\left( {m – 4} \right)^2} \le 28\)
Để \(M{A^2} – M{B^2} – M{C^2}\)đạt giá trị lớn nhất thì \(m = 4\)
15: Ta có \(\overrightarrow {AB} = \left( { – 1; – 1;2} \right),\,\overrightarrow {AC} = \left( {1; – 2;1} \right) \)
\(\Rightarrow {S_{ABC}} = \dfrac{1}{2}\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]} \right| = \dfrac{{3\sqrt 3 }}{2}\)
\(\overrightarrow {DC} = \left( { – 2; – 2;4} \right),\,\overrightarrow {AB} = \left( { – 1; – 1;2} \right) \)
\(\Rightarrow \overrightarrow {DC} = 2.\overrightarrow {AB} \)
\( \Rightarrow ABCD\) là hình thang và \({S_{ABCD}} = 3{S_{ABC}} = \dfrac{{9\sqrt 3 }}{2}\)
Vì \({V_{S.ABCD}} = \dfrac{1}{3}SH.{S_{ABCD}} \Rightarrow SH = 3\sqrt 3 \)
Lại có \(H\) là trung điểm của \(CD \Rightarrow H\left( {0;1;5} \right)\)
Gọi \(S\left( {a;b;c} \right) \)
\(\Rightarrow \overrightarrow {SH} = \left( { – a;1 – b;5 – c} \right)\)
\(\Rightarrow \overrightarrow {SH} = k\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = k\left( {3;3;3} \right) \)\(\,= \left( {3k;3k;3k} \right)\)
Suy ra \(3\sqrt 3 = \sqrt {9{k^2} + 9{k^2} + 9{k^2}} \Rightarrow k = \pm 1\)
+) Với \(k = 1 \Rightarrow \overrightarrow {SH} = \left( {3;3;3} \right) \)\(\,\Rightarrow S\left( { – 3; – 2;2} \right)\)
+) Với \(k = – 1 \Rightarrow \overrightarrow {SH} = \left( { – 3; – 3; – 3} \right) \Rightarrow S\left( {3;4;8} \right)\)
Suy ra \(I\left( {0;1;3} \right)\)
16: Đường thẳng\(AB\)cắt mặt phẳng \((Oyz)\) tại điểm \(M \Rightarrow M(0;y;z)\)
\( \Rightarrow \overrightarrow {MA} = (2; – 1 – y;7 – z),\)\(\,\overrightarrow {MB} = (4;5 – y; – 2 – z)\)
Từ \(\overrightarrow {MA} = k\overrightarrow {MB} \) ta có hệ \(\left\{ \begin{array}{l}2 = k.4\\ – 1 – y = k\left( {5 – y} \right)\\7 – z = k\left( { – 2 – z} \right)\end{array} \right. \Rightarrow k = \dfrac{1}{2}\)
17: \(D \in Oy \Rightarrow D(0;y;0)\)
Ta có: \(\overrightarrow {AB} = \left( {1; – 1;2} \right),\)\(\,\overrightarrow {AD} = \left( { – 2;y – 1;1} \right),\overrightarrow {AC} = \left( {0; – 2;4} \right)\)
\( \Rightarrow \left[ {\overrightarrow {AB} .\overrightarrow {AC} } \right] = \left( {0; – 4; – 2} \right) \)
\(\Rightarrow \left[ {\overrightarrow {AB} .\overrightarrow {AC} } \right].\overrightarrow {AD} = – 4y + 2\) \({V_{ABCD}} = 5 \)
\(\Leftrightarrow \dfrac{1}{6}\left| { – 4y + 2} \right| = 5 \Leftrightarrow y = – 7;y = 8\)
\( \Rightarrow {D_1}\left( {0; – 7;0} \right),\,{D_2}\left( {0;8;0} \right) \Rightarrow {y_1} + {y_2} = 1\)
18:
\(\left( {\dfrac{1}{3}; – \dfrac{1}{3}; – \dfrac{1}{3}} \right)\) có tâm \(\left( {\dfrac{5}{3};\dfrac{7}{3};\dfrac{7}{3}} \right)\) và bán kính \(\left( {1; – 2;1} \right)\)
\(d(M,(P)) = 3 > R = 2 \Rightarrow (P) \cap (S) = \emptyset .\)
\(\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 1 + 2t}\\{z = 1 + 2t}\end{array}} \right.,t \in \mathbb{R}.\) cắt \(A\left( {\dfrac{5}{3};\dfrac{7}{3};\dfrac{7}{3}} \right)\) theo giao tuyến là một đường tròn
Chọn đáp án B.
19: \((P)\) tiếp xúc \(M\left( { – \dfrac{{11}}{3};\dfrac{{14}}{3};\dfrac{{13}}{3}} \right)\) \(M\left( {\dfrac{{29}}{3}; – \dfrac{{26}}{3}; – \dfrac{7}{3}} \right)\)
Chọn đáp án B.
20: \((S)\) tiếp xúc \((P)\) \( \Rightarrow \)
\(M \in (d)\)
Chọn đáp án A.






