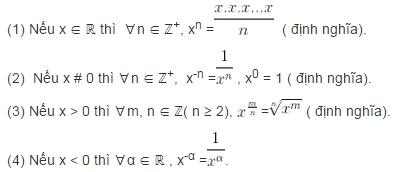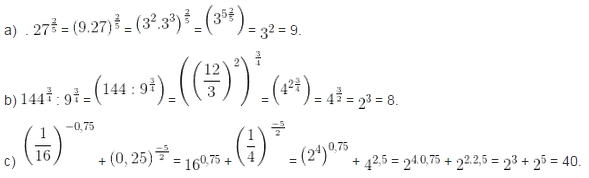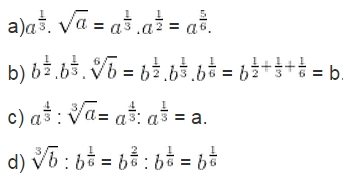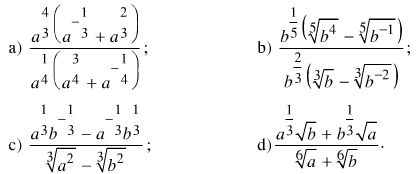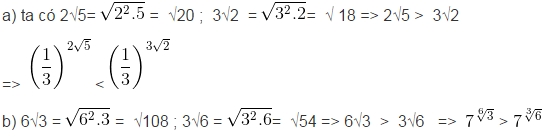Tóm tắt lý thuyết và hướng dẫn giải Bài 1,2 trang 55, bài 3,4,5 trang 56 SGK giải tích lớp 12: Lũy thừa – Chương 2 Hàm số lũy thừa – hàm số mũ và hàm số lôgarit
A. Tóm tắt lý thuyết: Lũy thừa
Khái niệm lũy thừa.
Lũy thừa là các biểu thức dạng xα, trong đó x,α là những số thực, x được gọi là cơ số, α được gọi là số mũ. Lũy thừa có các tính chất sau:
(5) ∀x, > 0, ∀α, β ∈ ,ℝ xα .xβ = xα+β; xα : xβ = xα-β; (xα)β = xαβ (tính chất các lũy thừa cùng cơ số).
(6)∀x,y > 0, ∀α ∈ ℝ (xy)α= xα.yα ; (x:y)α = xα: yα ( tính chất lũy thừa cùng số mũ).
(7) Nếu a> 1 thì ∀x1, x2 ∈ R, ax1>ax2 ⇔ x1 > x2 : nếu 0<a1, x2 ∈ ℝ , ax1 > ax2 ⇔ x1 < x2 ( so sánh hai lũy thừa cùng cơ số).
B. Giải bài tập 1,2,3,4,5 trang 55,56 SGK Giải Tích 12
Bài 1. Tính:
Đáp án bài 1: Có thể sử dụng máy tính cầm tay để thực hiện các phép tính. Sau đây là cách tính bằng cách sử dụng tính chất của lũy thừa:
Advertisements (Quảng cáo)
Bài 2. Cho a, b là những số thực dương. Viết các biểu thức dưới dạng lũy thừa với số mũ hữu tỉ:
Giải
Advertisements (Quảng cáo)
Bài 3. Viết các số sau theo thứ tự tăng dần:
Giải: Các em học sinh có thể sử dụng máy tính cầm tay để tính các lũy thừa rồi sắp thứ tự cho đúng. Tuy nhiên để rèn luyện các tính chất của lũy thừa các em nên giải bài toán như sau:
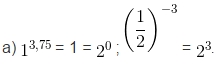 Mặt khác trong hai lũy thừa cungc cơ số lớn hơn 1, lũy thừa nào có số mũ lớn hơn là lũy thừa lớn hơn. Do đó theo thứ tự tăng dần ta được:
Mặt khác trong hai lũy thừa cungc cơ số lớn hơn 1, lũy thừa nào có số mũ lớn hơn là lũy thừa lớn hơn. Do đó theo thứ tự tăng dần ta được:
Bài 4. Cho a, b là những số thực dương. Rút gọn các biểu thức sau:
Đáp án bài 4:
Bài 5. Chứng minh rằng
Các em học sinh nên sử dụng các tính chất của lũy thừa để giải bài toán này