Đề kiểm tra 45 phút Chương 3 – Vecto trong không gian, quan hệ vuông góc trong không gian Hình học 11: Đường thẳng DB không vuông góc với đường thẳng nào sau đây?

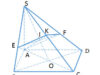
1. Cho hình chóp S. ABCD , đáy là hình thoi tâm O và SA =SC, SB = SD. Đường thẳng DB không vuông góc với đường thẳng nào sau đây?
A. AC.                B. SA.

C. SO.                D. SD.

2. Cho hình lập phương ABCDEFGH, góc giữa  đường thẳng EG và mặt phẳng (BCGF) là:

A. 0⁰                    B. 45⁰

C. 90⁰                  D. 30⁰.

3. Xét các mệnh đề sau:

1. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước .

2. Hai đường thẳng cùng vuông góc với một mặt phẳng thì song song với nhau.

3. Nếu một đường thẳng và một mặt phẳng cùng vuông góc với một đường thẳng  khác thì chúng song song với nhau.

4. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

Số mệnh đề đúng là:

A. 1                                B. 2

C. 3                                D. 4.

4. Cho véc tơ \(\overrightarrow a  \ne \overrightarrow 0 \) và hai véc tơ \(\overrightarrow b \,,\,\overrightarrow c \) không cùng phương. Nếu véc tơ \(\overrightarrow a \) vuông góc với cả hai véc tơ \(\overrightarrow b \,,\,\overrightarrow c \) thì ba véc tơ \(\overrightarrow a \,,\,\overrightarrow b \,,\,\overrightarrow c \) là:

A. Đồng phẳng.

B. Có thể đồng phẳng.

C. Không đồng phẳng.

D. Có thể không đồng phẳng.

5. Cho I là trung điểm của đoạn thẳng AB, khi đó với điểm M bất kì. Tìm mệnh đề đúng.

A. \(\overrightarrow {IA}  – \overrightarrow {IB}  = \overrightarrow 0 \).

B. \(\overrightarrow {MA}  + \overrightarrow {MB}  = 2\overrightarrow {MI} \).

C. \(\overrightarrow {MA}  + \overrightarrow {MB}  =  – 2\overrightarrow {MI} \).

D. \(\overrightarrow {MA}  – \overrightarrow {MB}  = 2\overrightarrow {MI} \).

6. Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD và DA. Véc tơ \(\overrightarrow {MN} \) cùng với hai vec tơ nào sau đây đồng phẳng ?

A. \(\overrightarrow {MA} \,,\,\overrightarrow {MQ} \).

B. \(\overrightarrow {MD} \,,\,\overrightarrow {MQ} \).

C. \(\overrightarrow {AC} \,,\,\overrightarrow {AD} \).

D. \(\overrightarrow {MP} \,,\,\overrightarrow {CD} \).

7. Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng AC và C’D’ bằng:

A. 0⁰                         B. 45⁰

C. 90⁰                       D. 60⁰.

8. Cho hình chóp S.ABCD có ABCD là hình vuông và \(SA \bot \left( {ABCD} \right)\). Khi đó, tam giác SBC là;

A. Tam giác thường.

B. Tam giác đều.

C. Tam giác cân

D. Tam giác vuông .

9. Cho hình tứ diện OABC có OA, OB, OC đôi một vuông góc . Nếu I là hình chiếu của điểm O trên mặt phẳng (ABC) thì I là:

A. Trọng tâm của tam giác ABC.

B. Trực tâm của tam giác ABC.

C. Tâm của đường tròn ngoại tiếp tam giác ABC.

D. Tâm của đường tròn nội tiếp tam giác ABC.

10. Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc. Khẳng định nào sau đây đúng?

A. \(AB \bot (ACD)\).             B. \(BC \bot (ACD)\).

C. \(CD \bot (ABC)\).             D. \(AD \bot (BCD)\)

11.  Cho hai vec tơ không cùng phương \(\overrightarrow a \,,\,\overrightarrow b \). Khi đó ba vec tơ \(\overrightarrow a \,,\,\overrightarrow b \,,\,\overrightarrow c \) đồng phẳng khi và chỉ khi có các số m và n sao cho;

A. \(\overrightarrow c  =  – m\overrightarrow a  + 2n\overrightarrow b \).

B. \(m\overrightarrow c  = n\overrightarrow a  + n\overrightarrow b \).

C. \(\overrightarrow c  = \overrightarrow a  + n\overrightarrow b \).

D. \(\overrightarrow c  = m\overrightarrow a  – n\overrightarrow b \)

12. Các đường thẳng cùng vuông góc với một đường thẳng thì:

A. Thuộc một mặt phẳng .

B. Vuông góc với nhau.

C. Song song với một mặt phẳng .

D. Song song với nhau.

13. Cho tứ diện ABCD có AB = AC = AD; góc BAC bằng góc BAD bằng 60⁰. Gọi M và N là trung điểm của AB và CD. Kết luận nào sau đây sai?

A. MN vuông góc với AB.

B. MN vuông góc với CD.

C. MN vuông góc với AB và CD.

D. MN không vuông góc với AB và CD.

14. Cho hình chóp S. ABCD có ABCD là hình chữ nhật. SA vuông góc với (ABCD), AH và AK lần lượt là đường cao của tam giác SAB và SAD. Hai mặt phẳng (SAC) và (AHK) vuông góc vì:

A. \(AH \bot (SBC)\) ( do \(AH \bot SB\,,\,\,AH \bot BC\)) và \(AK \bot (SCD)\,\left( {do\,AK \bot SD\,,\,AK \bot CD} \right)\)

B. \(AH \bot (SBC)\)( do \(AH \bot SB\,,\,AH \bot BC\)) và \(AK \bot (SCD)\,\) ( do \(AK \bot SD\,,\,\,AK \bot CD\)) nên \(SC \bot (AHK)\)

C. \(AH \bot (SBC)\) ( do \(AH \bot SB\,,\,AH \bot BC\)) nên \(SC \bot (AHK)\)

D. \(AK \bot (SBC)\) ( do \(AK \bot SD\,,\,AK \bot CD\)) nên \(SC \bot (AHK)\)

15. Mặt phẳng trung trực của đoạn thẳng AB là;

A. Luôn vuông góc với AB tại một điểm bất kì.

B. Luôn cách đều   hai đầu mút A và B.

C. Luôn vuông góc với AB tại trung điểm của AB.

D. Luôn song song với AB.

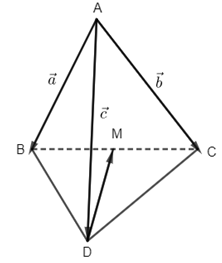
16. Cho tứ diện ABCD . Đặt \(\overrightarrow {AB}  = \overrightarrow a ,\overrightarrow {AC}  = \overrightarrow {b\,} \,,\,\overrightarrow {AD}  = \overrightarrow c \). Gọi M là trung điểm của BC. Trong các đẳng thức sau, đẳng thức nào đúng?

A. \(\overrightarrow {DM}  = \dfrac{1}{2}\left( {\overrightarrow a  + \overrightarrow c  – 2\overrightarrow b } \right)\).

B. \(\overrightarrow {DM}  = \dfrac{1}{2}\left( {\overrightarrow b  + \overrightarrow c  – 2\overrightarrow a } \right)\).

C. \(\overrightarrow {DM}  = \dfrac{1}{2}\left( {\overrightarrow a  + \overrightarrow b  – 2\overrightarrow c } \right)\).

D. \(\overrightarrow {DM}  = \dfrac{1}{2}\left( {\overrightarrow a  + 2\overrightarrow b  – \overrightarrow c } \right)\).

17. Cho hai điểm phân biệt A, B và một điểm O bất kì. Mệnh đề nào sau đây là đúng ?

A. Điểm M thuộc đường thẳng BA khi và chỉ khi \(\overrightarrow {OM}  = \overrightarrow {OB}  = k\overrightarrow {BA} \).

B. Điềm M thuộc đường thẳng AB khi và chỉ khi \(\overrightarrow {OM}  = \overrightarrow {OB}  = k\left( {\overrightarrow {OB}  – \overrightarrow {OA} } \right)\).

C. Điểm M thuộc đường thẳng AB khi và chỉ khi \(\overrightarrow {OM}  = k\overrightarrow {OA}  + \left( {1 – k} \right)\overrightarrow {OB} \).

D. Điểm M thuộc đường thẳng AB khi và chỉ khi \(\overrightarrow {OM}  = \overrightarrow {OA}  + \overrightarrow {OB} \)

18. Cho tứ diện SABC và I là trọng tâm tam giác ABC. Chọn đẳng thức đúng.

A. \(\overrightarrow {SI}  = \overrightarrow {SA}  + \overrightarrow {SB}  + \overrightarrow {SC} \).

B. \(\overrightarrow {SI}  = \dfrac{1}{3}\overrightarrow {SA}  + \dfrac{1}{3}\overrightarrow {SB}  + \dfrac{1}{3}\overrightarrow {SC} \).

C. \(3\left( {\overrightarrow {SA}  – \overrightarrow {SB}  + \overrightarrow {SC} } \right) = \overrightarrow {SI} \).

D. \(6\overrightarrow {SI}  = \overrightarrow {SA}  + \overrightarrow {SB}  + \overrightarrow {SC} \).

19. Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, BC, CD, và DA. Vecto \(\overrightarrow {MN} \) cùng với hai vecto nào sau đây là ba vecto đồng phẳng?

A. \(\overrightarrow {MA} \,,\,\overrightarrow {MQ} \).        B. \(\overrightarrow {MD} \,,\,\overrightarrow {MQ} \).

C. \(\overrightarrow {AC} \,,\,\overrightarrow {AD} \).         D. \(\overrightarrow {MP} \,,\,\overrightarrow {CD} \).

20. Cho hình lăng trụ ABC.A’B’D’, M là trung điểm của BB’. Đặt \(\overrightarrow {CA}  = \overrightarrow a \,,\,\overrightarrow {CB}  = \overrightarrow b \,,\,\overrightarrow {AA’}  = \overrightarrow c \). Khẳng định nào sau đây đúng?

A. \(\overrightarrow {AM}  = \overrightarrow b  + \overrightarrow c  – \dfrac{1}{2}\overrightarrow a \).

B. \(\overrightarrow {AM}  = \overrightarrow a  – \overrightarrow c  – \dfrac{1}{2}\overrightarrow b \).

C. \(\overrightarrow {AM}  = \overrightarrow a  + \overrightarrow c  – \dfrac{1}{2}\overrightarrow b \).

D. \(\overrightarrow {AM}  = \overrightarrow b  – \overrightarrow a  + \dfrac{1}{2}\overrightarrow c \).

21. Cho tứ diện ABCD . Người ta định nghĩa “ G là trọng tâm tứ diện ABCD khi\(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow 0 \). Khẳng định nào sau đây sai?

A. G là trung điểm của đoạn IJ ( I, J lần lượt là trung điểm AB vàCD)

B. G là trung điểm của đoạn thẳng nối trung điểm của AC và BD

C. G là trung điểm của đoạn thẳng nối trung điểm của AD và BC

D. Chưa thể xác định được.

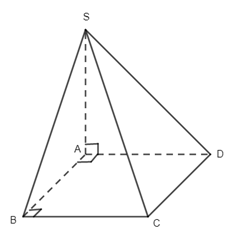
22. Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a. Gọi M và N lần lượt là trung điểm của AD và SD . Số đo của góc (MN, SC) bằng:

A. 30⁰                      B. 45⁰

C. 60⁰                      D. 90⁰.

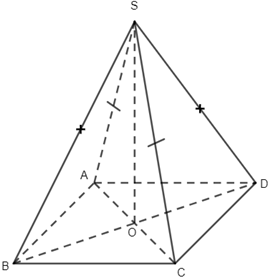
23. Cho hình chóp S.ABC có SA  = SB =  SC . Gọi O là hình chiếu của S lên mặt đáy ABC . Khẳng định nào sau đây là khẳng định đúng?

A. O là trọng tâm tam giác ABC .

B. O là tâm đường tròn ngoại tiếp tam giác ABC .

C. O là trực tâm tam giác ABC .

D. O là tâm đường tròn nội tiếp tam giác ABC .

24. Cho hình chóp S.ABC có S\(SA \bot \left( {ABC} \right)\,,\,AB \bot BC\). Gọi O là tâm đường tròn ngoại tiếp tam giác SBC . H là hình chiếu vuông góc của O lên ( ABC). Khẳng định nào sau đây đúng?

A. H là trung điểm cạnh AB .

B. H là trung điểm cạnh AC .

C. H là trọng tâm tam giác ABC .

D. H là tâm đường tròn ngoại tiếp tam giác ABC .

25. Cho tứ diện ABCD có AC =  AD và BC  = BD . Gọi I là trung điểm củaCD. Khẳng định nào sau đây sai ?

A. Góc giữa hai mặt phẳng (ACD) và (BCD) là góc AIB.

B. Góc giữa hai mặt phẳng (ABC) và (ABD) là góc CBD.

C. \(\left( {BCD} \right) \bot \left( {AIB} \right)\).

D. \(\left( {ACD} \right) \bot \left( {AIB} \right)\).

1.

Do ABCD là hình thoi tâm O nên \(AC \bot BD\) và O là trung điểm A.

Tam giác SBD cân tại S nên \(SO \bot BD\) , suy ra \(BD \bot \left( {SAC} \right)\). Do đó, \(BD \bot SA\) .

Vậy đáp án A, B, C đúng .

Chọn đáp án D.

2.

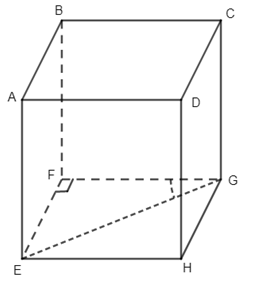
Do ABCD.EFGH là hình lâp phương nên ta có \(\left\{ \begin{array}{l}EF \bot FG\\EF \bot FB\end{array} \right.\, \Rightarrow EF \bot \left( {BCGF} \right)\) . Suy ra F là hình chiếu vuông góc của E xuống mặt phẳng (BCGF). Do vậy, \(\left( {EG,(BCGF)} \right) = \left( {EG,FG} \right) = \widehat {EGF} = {45^0}\)

6.

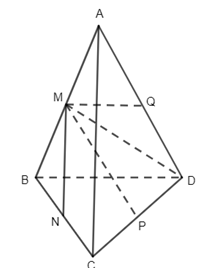
Do MN và AC cùng phương

Chọn đáp án C

7.

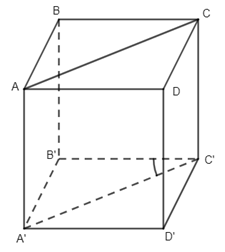
Do AC // A’C’ nên \(\left( {\widehat {AC,C’D’}} \right) = \left( {\widehat {A’C’,C’D’}} \right) = \widehat {A’C’D’} = {45^0}\)

Chọn đáp án B.

8.

Ta có \(\left\{ \begin{array}{l}BC \bot AB\\SA \bot BC\,(SA \bot (ABCD))\end{array} \right.\,\, \Rightarrow BC \bot (SAB)\,\, \Rightarrow BC \bot SB\) . do đó tam giác SBC là tam giác vuông.

Chọn đáp án D.

9.

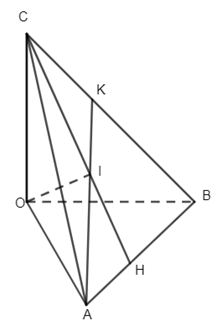
Giả sử AI cắt BC tại K, CI cát AB tại H.

Ta có \(\left\{ \begin{array}{l}AB \bot OI\,\,(\,\,OI \bot (ABC) \supset AB\\AB \bot OC\,\,(\,\,OC \bot (OAB) \supset AB\end{array} \right.\,\, \Rightarrow \,\,AB \bot \left( {OCH} \right)\,\, \Rightarrow AB \bot CH\)

Làm tương tự ta cũng có \(BC \bot AK\)

Do đó, I là trực tâm tam giác ABC.

Chọn đáp án B.

10.

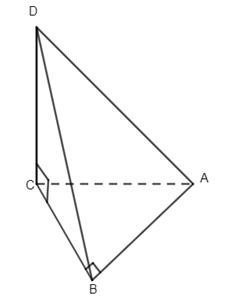
Đáp án A sai vì chỉ có \(AB \bot CD\) . Đáp án B sai vì chỉ có \(BC \bot CD\) . Đáp án C đúng vì \(\left\{ \begin{array}{l}CD \bot AB\\CD \bot BC\end{array} \right.\,\, \Rightarrow CD \bot \left( {ABC} \right)\) .

Đáp án D sai vì AD không vuông góc với đường thẳng nào thuộc (BCD).

13.

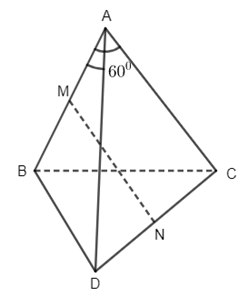
Do \(\overrightarrow {AB} .\overrightarrow {CD}  = \overrightarrow {AB} .\left( {\overrightarrow {AD}  – \overrightarrow {AC} } \right) = 0\,\, \Rightarrow \,\,\,AB \bot CD\) . Đáp án B sai.

Từ đó,  \(\overrightarrow {AB} .\overrightarrow {MN}  = \overrightarrow {AB} .\left( {\overrightarrow {CN}  – \overrightarrow {CM} } \right) = 0\),  đáp án A , C sai.

Chọn đáp án D.

16.

Ta có

\(\begin{array}{l}\overrightarrow {DM}  = \overrightarrow {DB}  + \overrightarrow {BM} \\\;\;\;\;\;\;\;\;\; = \overrightarrow {DA}  + \overrightarrow {AB}  + \dfrac{1}{2}\overrightarrow {BC}  \\\;\;\;\;\;\;\;\;\;=  – \overrightarrow {AD}  + \overrightarrow {AB}  + \dfrac{1}{2}\left( {\overrightarrow {BA}  + \overrightarrow {AC} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=  – \overrightarrow {AD}  + \dfrac{1}{2}\overrightarrow {AB}  + \dfrac{1}{2}\overrightarrow {AC} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=  – \overrightarrow c  + \dfrac{1}{2}\overrightarrow a  + \dfrac{1}{2}\overrightarrow b \,\, = \dfrac{1}{2}\left( {\overrightarrow a  + \overrightarrow b  – 2\overrightarrow c } \right)\end{array}\)

Chọn đáp án C.

18. Do I là trọng tâm tam giác ABC nên \(\overrightarrow {SA}  + \overrightarrow {SB}  + \overrightarrow {SC}  = 3\overrightarrow {SI} \,\, \Rightarrow \,\,\overrightarrow {SI}  = \dfrac{1}{3}\overrightarrow {SA}  + \dfrac{1}{3}\overrightarrow {SB}  + \dfrac{1}{3}\overrightarrow {SC} \)

Chọn đáp án B.

19.

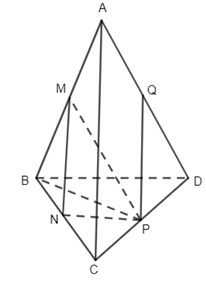
Do PQ //AC nên \(\overrightarrow {PQ} ,\overrightarrow {AC} \)  cùng phương , do đó đáp án C đúng.

20.

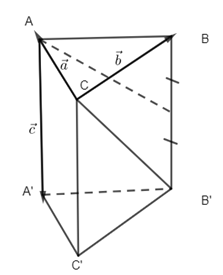
Ta có

\(\begin{array}{l}\overrightarrow {AM}  = \dfrac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AB’} } \right) = \dfrac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AA’}  + \overrightarrow {A’B’} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AA’}  + \overrightarrow {AB} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}\left( {2\overrightarrow {AB}  + \overrightarrow {AA’} } \right) =  – \overrightarrow {CA}  + \overrightarrow {CB}  + \dfrac{1}{2}\overrightarrow {AA’} \\ \Rightarrow \overrightarrow {AM}  =  – \overrightarrow a  + \overrightarrow b  + \dfrac{1}{2}\overrightarrow c \end{array}\)

Chọn đáp án D.

22.

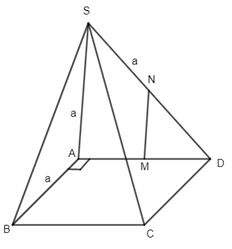
M, N là trung điểm của AD và SD nên ta có MN // SA, suy ra \(\left( {MN.SC} \right) = \left( {SA,SC} \right) = \widehat {ASC}\) .

Tam giác SAC có \(SA = a,SC = a,\,AC = \sqrt {{a^2} + {a^2}}  = a\sqrt 2 \) , suy ra tam giác SAC vuông tại S, tức là \(\widehat {ASC} = {90^0}\) . Chọn đáp án D.

23.

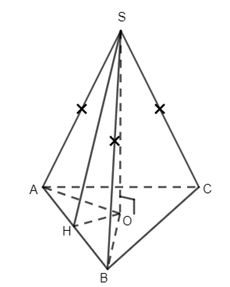
Lấy H là trung điểm của AB. Do tam giác SAB cân tại S nên \(SH \bot AB\). Lại có \(SO \bot \left( {ABC} \right)\, \Rightarrow \,\,SSO \bot AB\) . Từ đó suy ra \(AB \bot \left( {SOH} \right) \Rightarrow AB \bot OH\).

Tam giác OAB có OH vừa là đường cao vừa là dường trung tuyến nên tam giác OAB là tam  giác cân, suy ra OA = OB.

Làm tương tự ta với tam giác OAC, tam giác OBC ta cũng có OA = OC , OB = OC. Vậy OA = OB = OC hay O là tâm đường tròn ngoại tiếp tam giác ABC.

Chọn đáp án B.

24.

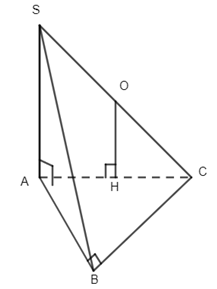
Ta có \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\,(SA \bot (ABC))\end{array} \right.\,\,\, \Rightarrow BC \bot (SAB)\,\, \Rightarrow BC \bot SB\) .

Do đó, tam giác SBC vuông tại B.

Suy ra đường tròn ngoại tiếp tam giác SBC là trung điểm cạnh huyền SC.

Từ O kẻ \(OH \bot AC\,\, \Rightarrow OH\,//\,SA\) ( do \(SA \bot AC\) ). Mà \(SA \bot (ABC)\, \Rightarrow OH \bot (ABC)\).

Vậy H là hình chiếu vuông góc của O lên (ABC).

Chọn đáp án B.

25.

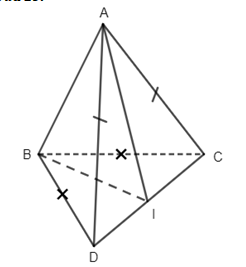
Ta có tam giác ACD cân tại A nên \(AI \bot CD\) . tam giác BCD cân tại B nên \(BI \bot CD\) . mà (BCD) và (ACD) có CD chung nên \(\left( {(ACD),(BCD)} \right) = \left( {BI,AI} \right) = \widehat {AIB}\).

Ta có

\(\begin{array}{l}\left\{ \begin{array}{l}CD \subset (BCD)\\CD \bot BI\\CD \bot AI\end{array} \right.\, \Rightarrow \,\,\left( {BCD} \right) \bot \left( {AIB} \right)\\\left\{ \begin{array}{l}CD \subset (ACD)\\CD \bot BI\\CD \bot AI\end{array} \right.\, \Rightarrow \,\,\left( {ACD} \right) \bot \left( {AIB} \right)\end{array}\)

Chọn đáp án B.