
1. Cho hình hộp ABCD. A’B’C’D’. M là điểm trên AC sao cho \(\overrightarrow {AC} = 3\overrightarrow {MC} \). Lấy N trên đoạn C’D sao cho \(\overrightarrow {DN} = x\overrightarrow {DC’} \). Với giá trị nào của x thì \(\overrightarrow {MN\,} \,,\,\,\overrightarrow {BD’} \) cùng phương ?
A. \(x = \dfrac{1}{3}\). B. \(x = \dfrac{1}{4}\).
C. \(x = \dfrac{2}{3}\). D. \(x = 3\).
2. Cho hình lập phương ABCD.EFGH. Góc giữa hai véc tơ \(\overrightarrow {AB} \,,\,\overrightarrow {EG} \) bằng ;
A. 600 B. 450
C. 300 D. 900.
3. Trong không gian cho ba đường thẳng a, b, c. Khẳng định nào sau đây sai ?
A. Nếu a // b và \(c \bot a\) thì \(c \bot b\).
B. Nếu \(a \bot \left( \alpha \right)\) và b // \(\left( \alpha \right)\) thì \(a \bot b\).
C. Nếu \(a \bot b\,,\,c \bot b\) và a cắt c thì \(b \bot \left( {a,c} \right)\).
D. Nếu \(a \bot b\,,\,b \bot c\) thì \(a \bot c\).
4. Cho hình hộp ABCD.A’B’C’D’. Rút gọn hệ thức \(\overrightarrow {AB} + \overrightarrow {B’D’} – \overrightarrow {B’A} \) ta được véc tơ nào sau đây?
A. \(\overrightarrow {AC’} \). B. \(\overrightarrow {AD’} \).
C. \(\overrightarrow {BC’} \). D. \(\overrightarrow {DC’} \).
5. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, SA vuông góc với mặt phẳng (ABCD). Chọn khẳng định đúng.
A. O là hình chiếu vuông góc của S lên mặt phẳng (ABCD).
B. A là hình chiếu vuông góc của C lên mp (SAB).
C. Trung điểm của AD là hình chiếu vuông góc của C lên mp (SAD).
D. O là hình chiếu vuông góc của B lên mp (SAC).
6. Trong các mệnh đề sau, mệnh đề nào sai?
A. Trong không gian, hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
B. Trong mặt phẳng, hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song với nhau.
C. Trong không gian cho hai đường thẳng song song. Đường thẳng nào vuông góc với đường thẳng này thì vuông góc với đường thẳng kia.
D. Trong không gian, hai đường thẳng vuông góc với nhau thì có thể cắt nhau hoặc chéo nhau.
7. G là trọng tâm của tam giác ABC. Tìm phát biểu sai.
A. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \).
B. \(\overrightarrow {GA} + \overrightarrow {GB} = \overrightarrow {CG} \).
C. \(\overrightarrow {AG} + \overrightarrow {BG} + \overrightarrow {CG} = \overrightarrow 0 \).
D. \(\overrightarrow {GA} = \overrightarrow {GB} – \overrightarrow {GC} \).
8. Cho hình lập phương ABCD.EFGH, góc giữa hai đường thẳng AB và GC là:
A. 00 B. 450
C. 1800 D. 900.
9. Cho tứ diện ABCD và \(\overrightarrow {AB} = \overrightarrow a \,,\,\overrightarrow {AC} = \overrightarrow b \,,\,\overrightarrow {AD} = \overrightarrow c \). Gọi M, N , P và Q lần lượt là trung điểm của AB, BC, CD, DA.Bốn điểm M, N, P, Q cùng thuộc một mặt phẳng vì:
A. \(\overrightarrow {MP} = \dfrac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {AD} – \overrightarrow {AB} } \right)\).
B. \(\overrightarrow {MP} = \overrightarrow {MB} + \overrightarrow {BP} \).
C. \(\overrightarrow {MP} = \dfrac{1}{2}\left( {\overrightarrow {MN} + \overrightarrow {MQ} } \right)\).
D. \(\overrightarrow {MP} = \overrightarrow {MN} + \overrightarrow {MQ} \).
10. Cho vec tơ \(\overrightarrow n \ne \overrightarrow 0 \) và hai vec tơ \(\overrightarrow a \,,\,\overrightarrow b \) không cùng phương . Nếu vec tơ \(\overrightarrow n \) vuông góc với cả hai vec tơ \(\overrightarrow a \,,\,\overrightarrow b \) thì \(\overrightarrow a \,,\,\overrightarrow b \,,\,\overrightarrow n \) :
A. Đồng phẳng.
B. Không đồng phẳng.
C. Có thể đồng phẳng
D. Có thể không đồng phẳng.
11. Cho hình lập phương ABCD. A’B’C’D’. Hình chiếu vuông góc của A lên mặt phẳng (A’BD) là:
A. Trung điểm của BD.
B. Trung điểm của A’B.
C. Trung điểm của A’D.
D. Tâm O của tam giác BDA’.
12. Chọn mệnh đề đúng trong các mệnh đề sau đây:
A.Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
B. Cho hai đường thẳng chéo nhau a và b đồng thời \(a \bot b\) . Luôn có mặt phẳng \(\left( \alpha \right)\) chứa a và \(\left( \alpha \right) \bot b\).
C. Cho hai đường thẳng a và b vuông góc với nhau. Nếu mặt phẳng \(\left( \alpha \right)\) chứa a và mặt phẳng \(\left( \beta \right)\) chứa b thì \(\left( \alpha \right) \bot \left( \beta \right)\).
D. Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một đường thẳng khác.
13. Đường thẳng AB song song với mặt phẳng (P) khi:
A. Trong (P) có \(\overrightarrow a \) cùng phương với \(\overrightarrow {AB} \).
B. Trong (P) có \(\overrightarrow a \) cùng phương với \(\overrightarrow {AB} \) và hai đầu mút của \(\overrightarrow a \) không thuộc đường thẳng AB.
C. Trong (P) có hai vec tơ phân biệt cùng phương với \(\overrightarrow {AB} \).
D. Trong (P) có hai vec tơ phân biệt \(\overrightarrow a \,,\,\overrightarrow b \) cùng phương với \(\overrightarrow {AB} \), ngoài ra ba vec tơ \(\overrightarrow a \,,\,\overrightarrow b \,,\,\overrightarrow {AB} \) không đồng phẳng.
14. Cho tứ diện ABCD. Nếu \(AB \bot CD\,,\,AC \bot BD\,,\,BC \bot AD\) thì:
A. \(\overrightarrow {AB} .\overrightarrow {AC} \ne \overrightarrow {AC} .\,\overrightarrow {AD} = \overrightarrow {AB} .\overrightarrow {AD} \).
B. \(\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AC} .\overrightarrow {AD} \ne \overrightarrow {AB} .\overrightarrow {AD} \).
C. \(\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AC} .\overrightarrow {AD} = \overrightarrow {AB} .\overrightarrow {AD} \).
D. \(\overrightarrow {AB} .\overrightarrow {AC} \ne \overrightarrow {AC} .\overrightarrow {AD} \ne \overrightarrow {AB} .\overrightarrow {AD} \).
Advertisements (Quảng cáo)
15. Cho hình tứ diện OABC có OA, OB, OC đôi một vuông góc . Gọi I là hình chiếu của điểm O trên mặt phẳng (ABC). Tam giác ABC là
A. Tam giác vuông.
B. Tam giác có một góc tù.
C. Tam giác cân đỉnh A.
D. Tam giác có ba góc nhọn.
16. Cho hình lập phương ABCD.A1B1C1D1. Gọi O là tâm của hình lập phương. Chọn đẳng thức đúng.
A. \(\overrightarrow {AO} = \dfrac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A_1}} } \right)\).
B. \(\overrightarrow {AO} = \dfrac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A_1}} } \right)\).
C. \(\overrightarrow {AO} = \dfrac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A_1}} } \right)\).
\(D. \overrightarrow {AO} = \dfrac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A_1}} } \right)\).
17. Cho hình hộp ABCD.A1B1C1D1 với tâm O. Hãy chỉ ra đẳng thức sai?
A. \(\overrightarrow {A{C_1}} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A_1}} \).
B. \(\overrightarrow {AB} + \overrightarrow {B{C_1}} + \overrightarrow {CD} + \overrightarrow {{D_1}A} = \overrightarrow 0 \).
C. \(\overrightarrow {AB} + \overrightarrow {A{A_1}} = \overrightarrow {AD} + \overrightarrow {D{D_1}} \).
\(D. \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {C{C_1}} = \overrightarrow {A{D_1}} + \overrightarrow {{D_1}O} + \overrightarrow {O{C_1}} .\)
18. Cho hình chóp S. ABCD có đáy là ABCD là hình bình hành. Đặt \(\overrightarrow {SA} = \overrightarrow a \,,\,\overrightarrow {SB} = \overrightarrow b \,,\,\overrightarrow {SC} = \overrightarrow c \,,\,\overrightarrow {SD} = \overrightarrow d \). Khẳng định nào sau đây đúng?
A. \(\overrightarrow a + \overrightarrow c = \overrightarrow b + \overrightarrow d \).
B. \(\overrightarrow a + \overrightarrow b = \overrightarrow c + \overrightarrow d \).
C. \(\overrightarrow a + \overrightarrow d = \overrightarrow c + \overrightarrow b \).
D. \(\overrightarrow a + \overrightarrow c + \overrightarrow b + \overrightarrow d = \overrightarrow 0 \).
19. Trong không gian cho ba đường thẳng phân biệt a, b, c . Khẳng định nào sau đây sai?
A. Nếu a và b cùng nằm trong một mặt phẳng và cùng vuông góc với c thì a//b .
B. Nếu a//b và \(c \bot a\) thì \(c \bot b\).
C. Nếu góc giữa a và c bằng góc giữa b và c thì a//b .
D. Nếu a và b cùng nằm trong mp (a)//c thì góc giữa a và c bằng góc giữa b và c .
20. Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\) và \(\Delta \)ABC vuông ở B . Gọi AH là đường cao của \(\Delta \)SAB . Khẳng định nào sau đây sai?
A. \(SA \bot BC\). B. \(AH \bot BC\).
C. \(AH \bot AC\). D. \(AH \bot SC\).
21. Cho hình chóp S.ABCD có đáy ABCD là hình vuông và \(SA \bot \left( {ABCD} \right)\). Gọi I, J , K lần lượt là trung điểm của AB, BC và SB . Khẳng định nào sau đây là khẳng định sai?
A. \(\left( {IJK} \right)//\left( {SAC} \right)\).
B. \(BD \bot \left( {IJK} \right)\).
C. Góc giữa SC và BD có số đo là 600,
D. \(BD \bot \left( {SAC} \right)\).
22. Cho tứ diện ABCD có cạnh AB,BC,BD bằng nhau và vuông góc với nhau từng đôi một. Khẳng định nào sau đây là khẳng định đúng?
A. Góc giữa AC và (BCD) là góc\(\widehat {ACD}\).
B. Góc giữa AD và ( ABC) là góc \(\widehat {ADB}\).
C. Góc giữa AC và ( ABD) là góc\(\widehat {CAB}\).
D. Góc giữa CD và (ABD )là góc \(\widehat {CBD}\).
23. Cho hình lăng trụ ABCD.A’B’C ‘D’ . Hình chiếu vuông góc của A’ lên (ABC) trùng với trực tâm H của tam giác ABC . Khẳng định nào sau đây không đúng?
A. \(\left( {AA’B’B} \right) \bot \left( {BB’C’C} \right)\).
B. \(\left( {AA’H} \right) \bot \left( {A’B’C’} \right)\).
C. \(\left( {BB’C’C} \right) \bot \left( {AA’H} \right)\).
D. BB’C’C là hình chữ nhật.
Advertisements (Quảng cáo)
24. Cho hình lập phương ABCD.A’B’C ‘D’ cạnh bằng a . Khẳng định nào sau đây sai?
A. Hai mặt (ACC ‘ A’ ) và (BDD’B’) vuông góc nhau
B. Bốn đường chéo AC ‘, A’C,BD’, B’D bằng nhau và bằng \(a\sqrt 3 \).
C. Hai mặt (ACC ‘ A’) và (BDD’B’) là hai hình vuông bằng nhau.
D. \(AC \bot BD’\).
25. Cho hình thoi ABCD có cạnh bằng a và\(\widehat A = {60^0}\). Trên đường thẳng vuông góc với mặt phẳng (ABCD) tại O (O là tâm của ABCD), lấy điểm S sao cho tam giác SAC là tam giác đều. Khẳng định nào sau đây đúng?
A. S.ABCD là hình chóp đều
B. Hình chóp S.ABCD có các mặt bên là các tam giác cân.
C. \(SO = \dfrac{{3a}}{2}\).
D. SA và SB hợp với mặt phẳng (ABCD) những góc bằng nhau.

|
Câu |
1 |
2 |
3 |
4 |
5 |
|
Đáp án |
A |
B |
D |
A |
D |
|
Câu |
6 |
7 |
8 |
9 |
10 |
|
Đáp án |
A |
D |
D |
D |
B |
|
Câu |
11 |
12 |
13 |
14 |
15 |
|
Đáp án |
D |
B |
D |
C |
D |
|
Câu |
16 |
17 |
18 |
19 |
20 |
|
Đáp án |
C |
C |
A |
D |
C |
|
Câu |
21 |
22 |
23 |
24 |
25 |
|
Đáp án |
C |
C |
A |
C |
C |
1.
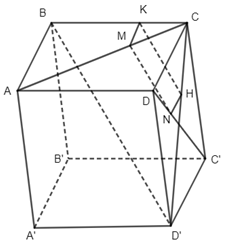
Lấy K là điểm thuộc BC sao cho \(\overrightarrow {BC} = 3\overrightarrow {KC} \) , lấy H thuộc CD’ sao cho\(\overrightarrow {D’C} = 3\overrightarrow {HC} \) . Với \(x = \dfrac{1}{3}\) thì ta có \(NH\, = \dfrac{1}{3}CD = KM,\,NH//\,KM\) nên KMNH là hình bình hành. Do đó MN // KH mà KH // BD’, suy ra BD’ // MN \( \Rightarrow \overrightarrow {MN} ,\,\overrightarrow {BD’} \) cùng phương.
Chọn đáp án A.
2.

Ta có \(\overrightarrow {EG} = \overrightarrow {AC} \, \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {EG} } \right) = \left( {\overrightarrow {AB} ,\,\overrightarrow {AC} } \right) = \widehat {BAC} = {45^0}\)
Chọn đáp án B.
4.

Ta có \(\overrightarrow {AB} – \overrightarrow {B’D’} – \overrightarrow {B’A} = \overrightarrow {AB} – \left( {\overrightarrow {AD’} – \overrightarrow {AB’} } \right)\)
5.
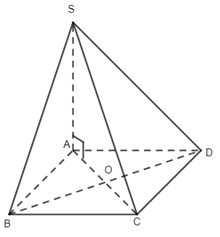
Ta có \(SA \bot (ABCD)\) nên hình hiếu vuông góc của S lên (ABCD) là A.
ABCD là hình thoi nên \(AC \bot BD\) , suy ra tam giác ABO vuông tại O nên góc \(\widehat {BAO}\) không vuông, do đó CA không vuông góc với AB, tức là AC không vuông góc với mp (SAB), A không là hình chiếu của C lên (SAB).
Ta có \(\left\{ \begin{array}{l}BO \bot AC\\BO \bot SA\end{array} \right.\, \Rightarrow \,\,BO \bot (SAC)\,\) nên O là hình chiếu vuông góc của B lên (SAC).
Chọn đáp án D.
7. Do G là trọng tâm tam giác ABC nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \, \Rightarrow \,\,\overrightarrow {AG} + \overrightarrow {BG} + \overrightarrow {CG} = \overrightarrow 0 \).
Từ đó ta cũng có \(\overrightarrow {GA} + \overrightarrow {GB} = – \overrightarrow {GC} = \overrightarrow {CG} \).
Chọn đáp án D.
8.
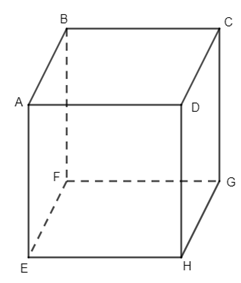
Do ABCD.EFGH là hình lập phương nên ta có \(CG \bot CD,\,CD\,//\,AB\,\, \Rightarrow CG \bot AB\).
Chọn đáp án D.
9. Ta có \(\overrightarrow {MP} = \overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MN} + \overrightarrow {MQ} \) ( do NP và MQ cùng song song và bằng nửa BD).
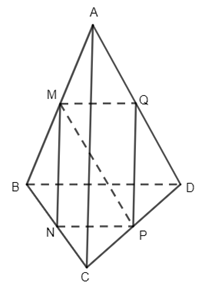
Chọn đáp án D.
11.
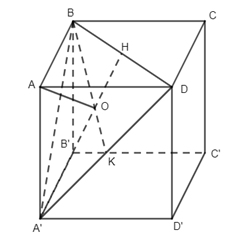
Lấy O là tâm tam giác BDA’, do tam giác BDA’đều ( có các cạnh là đường chéo của các hình vuông cạnh bằng nhau) nên tâm O là trọng tâm cũng là giao ba đường cao. Ta có \(\begin{array}{l}BD \bot AH,\,BD \bot AA’\, \Rightarrow BD \bot \left( {AA’H} \right) \Rightarrow BD \bot AO\\A’D \bot BK,\,A’D \bot AB\,\, \Rightarrow A’D \bot \left( {ABK} \right) \Rightarrow \,A’D \bot AO\\ \Rightarrow AO \bot (BDA’)\end{array}\)
Vậy tâm O của tam giác BDA’ là hình chiếu vuông góc của A lên mp (BDA’).
Chọn đáp án D.
14.
Ta có
\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow {AC} .\overrightarrow {BD} = \overrightarrow {AD} .\overrightarrow {CB} = 0\\\,\, \Rightarrow \,\,\overrightarrow {AB} \left( {\overrightarrow {AD} – \overrightarrow {AC} } \right) = \overrightarrow {AC} \left( {\overrightarrow {AD} – \overrightarrow {AB} } \right) = \overrightarrow {AD} \left( {\overrightarrow {AB} – \overrightarrow {AC} } \right) = 0\\\,\, \Rightarrow \,\,\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AC} .\overrightarrow {AD} = \overrightarrow {AB} .\overrightarrow {AD} \end{array}\)
Chọn đáp án C.
15.
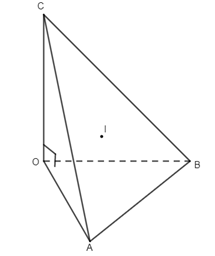
Giả sử tam giác ABC vuông tại A. Khi đó có hai đường thẳng BO và BA cùng vuông góc với mặt phẳng (OCA). Điều này vô lí, do đó tam giác ABC không thể là tam giác vuông. Từ O hạ \(OH \bot AB\,\, \Rightarrow CH \bot AB\) (theo định lí ba đường vuông góc). Vì điểm H nằm giữa hai điểm A và B nên tam giác ABC không thể có góc tù. Suy ra ABC có ba góc nhọn
Chọn đáp án D.
16.
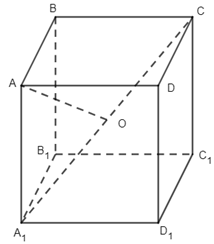
Ta có \(\overrightarrow {AO} = \dfrac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {A{A_1}} } \right) = \dfrac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A_1}} } \right)\). Chọn đáp án A.
17.
Ta có
\(\begin{array}{l}\overrightarrow {A{C_1}} = \overrightarrow {AC} + \overrightarrow {A{A_1}} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A_1}} \\\overrightarrow {AB} + \overrightarrow {B{C_1}} + \overrightarrow {CD} + \overrightarrow {{D_1}A} = \overrightarrow {A{C_1}} + \overrightarrow {CD} + \overrightarrow {{D_1}A} = \overrightarrow {{D_1}{C_1}} + \overrightarrow {CD} + \overrightarrow 0 \\\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {C{C_1}} = \overrightarrow {A{C_1}} \\\overrightarrow {A{D_1}} + \overrightarrow {{D_1}O} + \overrightarrow {O{C_1}} = \overrightarrow {A{C_1}} \\ \Rightarrow \,\,\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {C{C_1}} = \overrightarrow {A{D_1}} + \overrightarrow {{D_1}O} + \overrightarrow {O{C_1}} \\\overrightarrow {AB} + \overrightarrow {A{A_1}} = \overrightarrow {A{B_1}} ,\,\,\overrightarrow {AD} + \overrightarrow {D{D_1}} = \overrightarrow {A{D_1}} \end{array}\)
Chọn đáp án C.
18.
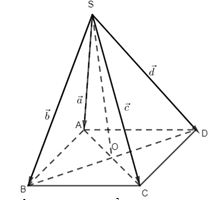
Lấy O là giao điểm của AC và BD. Do ABCD là hình bình hành nên O là trung điểm của AC và BD.
Ta có \(\overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} ,\,\,\overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} \)
\(\Rightarrow \,\,\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \)
\(\Rightarrow \,\,\overrightarrow a + \overrightarrow c = \overrightarrow b + \overrightarrow d \)
Chọn đáp án A.
20.
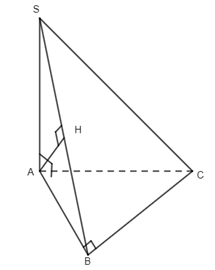
Ta có
\(\begin{array}{l}SA \bot (ABC)\, \Rightarrow \,\,SA \bot BC,\\ \left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right.\,\, \Rightarrow \,\,BC \bot (SAB)\, \Rightarrow BC \bot AH\\SB \bot AH\, \Rightarrow AH \bot (SBC)\, \Rightarrow AH \bot SC\end{array}\)
Chọn đáp án C.
21.
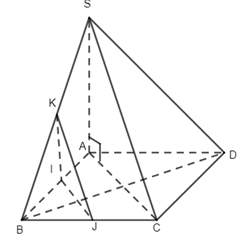
Ta có KJ // SC nên KJ //(SAC), KI //SA nên KI // (SAC), suy ra (IJK) // (SAC).
\(\begin{array}{l}\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\,\,(SA \bot (ABCD))\end{array} \right.\, \Rightarrow \,\,BD \bot (SAC)\\(IJK)//\,(SAC)\,\, \Rightarrow \,\,BD \bot (IJK)\end{array}\)
Chọn đáp án C.
22.
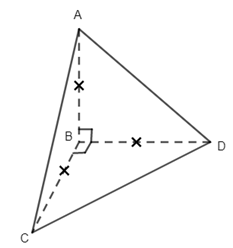
Ta có
\(\begin{array}{l}\left\{ \begin{array}{l}AB \bot BC\\AB \bot BD\end{array} \right.\, \Rightarrow AB \bot (BDC) \Rightarrow \left( {AC,(BCD)} \right) = \left( {AC,BC} \right) = \widehat {ACB}\\\left\{ \begin{array}{l}BD \bot BC\\BD \bot BA\end{array} \right.\, \Rightarrow BD \bot (ABC) \Rightarrow \left( {AD,(ABC)} \right) = \left( {AD,BA} \right) = \widehat {DAB}\\\left\{ \begin{array}{l}BC \bot BA\\BC \bot BD\end{array} \right.\, \Rightarrow BC \bot (ABD) \Rightarrow \left( {AC,(ABD)} \right) = \left( {AC,AB} \right) = \widehat {BAC}\\BC \bot (ABD)\, \Rightarrow \left( {CD,(ABD)} \right) = \left( {CD,BD} \right) = \widehat {CDB}\end{array}\)
Chọn đáp án C.
23.
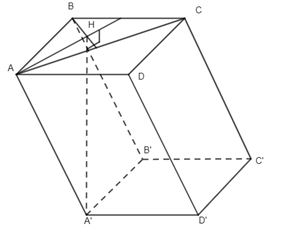
Ta có
\(\begin{array}{l}\left\{ \begin{array}{l}A’H \bot BC\\A’H \bot AB\end{array} \right. \Rightarrow A’H \bot (ABCD),\\ (ABCD)//(A’B’C’D’) \Rightarrow \,A’H \bot (A’B’C’D’)\\ \Rightarrow \,\,(HAA’) \bot (A’B’C’D’)\\\left\{ \begin{array}{l}AH \bot BC\\A’H \bot BC\end{array} \right. \Rightarrow BC \bot (HAA’) \Rightarrow \,(BCC’B’) \bot (HAA’)\\BC \bot (HAA’)\, \Rightarrow BC \bot AA’ \Rightarrow BC \bot BB’.\end{array}\)
Suy ra BCC’B’ là hình chữ nhật.
\(BC \bot AH,\,AH \ne AB\) nên ta có BC và AB không vuông góc với nhau. Do đó (BCC’B’) và (ABB’A’) không vuông góc với nhau.
Chọn đáp án A.
24.
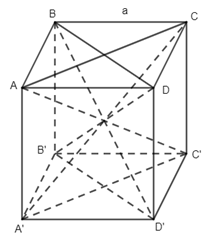
Ta có ABCD.A’B’C’D’ là hình lập phương nên \(\begin{array}{l}AC \bot BD,\,AC \bot DD’\, \Rightarrow AC \bot (BDD’B’) \Rightarrow \,\,(ACC’A’) \bot (BDD’B’)\\AC \bot (BDD’B’)\, \Rightarrow AC \bot BD’\end{array}\)
Bốn đường chéo AC’, A’C, BD’, D’B đều là cạnh huyền của tam giác có hai cạnh bên bằng \(a,\,a\sqrt 2 \) nên có độ dài bằng \(a\sqrt 3 \).
Hai mặt (ACC’A’) và (BDD’B’) là hai hình chữ nhật do có hai cạnh bằng a, hai cạnh bằng \(a\sqrt 2 \)
Chọn đáp án C.
25.
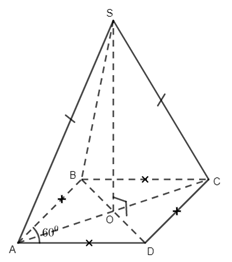
Do ABCD là hình thoi có góc A bằng 600 nên S.ABCD không là hình chop đều.
S.ABCD có SA = SC, SB = SD nhưng \(SA \ne SB\) nên các mặt bên không là tam giác cân.
Xét tam giác AOD vuông tại O, có
\(\begin{array}{l}\cos {30^0} = \dfrac{{OA}}{{AD}} = \dfrac{{OA}}{a} = \dfrac{{\sqrt 3 }}{2}\, \Rightarrow OA = \dfrac{{a\sqrt 3 }}{2}\\ \Rightarrow SO = \sqrt {S{A^2} – O{A^2}} = \sqrt {A{C^2} – O{A^2}} = \sqrt {3{a^2} – \dfrac{{3{a^2}}}{4}} = \dfrac{{3a}}{2}\end{array}\)
SA và SB hớp với (ABCD) các góc \(\widehat {SAO},\,\widehat {SBO}\). Do OA, OB không bằng nhau nên hai góc không bằng nhau.
Chọn đáp án C.





![[Lương Ngọc Quyến] Đề thi học kì II Toán 11: Tìm số hạng đầu, công sai và tổng](https://dethikiemtra.com/wp-content/uploads/2017/04/de-thi-hoc-ki-2-lop-11-mon-toan-100x75.png)
