Giải bài 1,2,3,4, 5,6,7 ,8,9,10,11 trang 59,60 SGK hình học 10: Các hệ thức lượng trong tam giác và giải tam giác

Các hệ thức lượng trong tam giác và giải tam giác

Đáp án và hướng dẫn giải bài 1,2,3,4,5,6,7,8,9 trang 59; bài 10,11 trang 60 SGK Hình học 10- Chương 2.

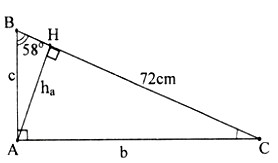
Bài 1. Cho ΔABC vuông tại A, góc B = 58⁰và cạnh a = 72 cm. Tính góc C, cạnh b, cạnh c và đường cao h_a

* ∠C = 180° – (∠A + ∠B) = 180° – (90° + 58°)
= 180° – 148° = 32°

* b = AC = BC.sinB = 72.sin58° ≈ 61,06 (cm)
* c = AB = BC.cosB = 72.sin58° ≈ 61,06 (cm)
* c = AB = BC.cosB = 72.cos58° ≈ 38,15 (cm)
* ha =AH = AB.sin58° = 38,15.sin58° ≈ 32,36 (cm)

Bài 2. Cho ΔABC biết các cạnh a = 52, 1cm; b = 85cm và c = 54cm. Tính các góc A, B, C.

Từ định lí cosin a² = b² + c²– 2bc. cosA

=> cosA ≈ 0,8089 => góc A = 36⁰

Bài 3.Cho ΔABC có ∠A = 120⁰cạnh b = 8cm và c = 5cm. Tính cạnh a, và góc ∠B, ∠C của Δ đó.

Giải: a²= 8² + 5²– 2.8.5 cos 120⁰= 64 + 25 + 40 = 129

=> a = √129 ≈ 11, 36cm

Ta có thể tính góc B theo định lí cosin

Ta cũng có thể tính góc B theo định lí sin :

Bài 4 trang 59. Tính diện tích S của tamgiác có số đo các cạnh lần lượt là 7, 9 và 12.

Dùng công thức Hê rông:

Advertisements (Quảng cáo)

Ta có 2p = 7 + 9 + 12 => p = 14

p – a = 14 – 7 = 7

p – b = 14 – 9 = 5

p – c = 14 – 12 = 2

≈ 31,3 (đvdt)

Bài 5. Δ ABC , có góc A = 120⁰. Tính cạnh BC cho biết cạnh AC = m và AB = n.

Ta có: BC² = AC² + AB²– 2AB.AC. cos120⁰

=> BC² = m² + n²– 2m.n (-1/2)

=> BC² = m² + n²+ m.n

Bài 6 trang 59 Hình 10. ΔABC có các cạnh a = 8cm, b = 10cm, c = 13cm

Advertisements (Quảng cáo)

a) Tam giác đó có góc tù không?

b) Tính độ dài đường trung tuyến MA của ΔABC đó.

Giải: a) Xét tổng a^{2 +} b² – c²= 8^{2 +} 10² – 13²= -5 < 0

Vậy tamgiác này có góc C tù

b) Áp dụng công thức tính đường trung tuyến, ta tính được AM ≈ 10,89cm

Bài 7. Tính góc lớn nhất của ΔABC biết:

a) Các cạnh a = 3cm, b = 4cm, c = 6cm

b) Các cạnh a = 40cm, b = 13cm, c = 37cm

Ta biết trong tam giác thì đối diện với cạnh lớn nhất là góc lớn nhất, vậy trong câu a) góc lớn nhất là góc C còn trong câu b) góc lớn nhất là góc A

Bài 8 trang 59. Cho ΔABC biết cạnh a = 137,5cm; ∠B = 83^{0 ; ∠C} = 57⁰. Tính góc A, cạnh b và c của tam giác.

Giải: Ta có: ∠A = 180⁰– (∠B + ∠C) = 40⁰

Áp dụng định lí sin :

Bài 9 trang 59 Hình 10. Cho hình bình hành ABCD có AB = a, BC = b ,BD = m, và AC = n. Chứng minh rằng: m²+ n² = 2(a² + b²)

Xét ΔABC: BO là đường trung tuyến

Bài 10 trang 60. Hai chiếc tàu thủy P và Q cách nhau 300m.TỪ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển người ta nhìn chiều cao AB của tháp dưới các góc BPA = 35⁰ góc BQA = 48⁰

Tính chiều cao của tháp.

Đáp án:

Bài 11. Muốn đo chiều cao của tháp Chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm A và B trên mặt đất có khoảng cách AB = 12cm cùng thẳng hàng với chân C của tháp để đặt hai giác kế. Chân của giác kế có chiều cao h = 1,3cm. Gọi D là đỉnh tháp và hai điểm A_1,B₁, cùng thẳng hàng với C₁thuộc chiều cao CD của tháp. Người ta đo được góc DA1C1 = 49⁰và góc DB1C1 = 35^0.

Tính chiều cao của CD của tháp đó.