Bài 61,62,63,64 trang 91,92 SGK Toán 9 tập 2: Đường tròn ngoại tiếp. Đường tròn nội tiếp

Tóm tắt lý thuyểt và hướng dẫn giải Bài 61, 62 trang 91; Bài 63, 64 trang 92 SGK Toán 9 tập 2: Đường tròn ngoại tiếp. Đường tròn nội tiếp – Chương 3 hình.

1. Định nghĩa 

a) Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác và đa giác này gọi là nội tiếp đường tròn.

b) Đường tròn tiếp xúc với tất cả các cạnh của một đa giác được gọi là đường tròn  nội tiếp đa giác và đa giác được gọi là ngoại tiếp đường tròn.

2. Định lí

Bất kì đa giác đều nào cũng có một đường tròn ngoại tiếp và một đường tròn nội tiếp

Tâm của một đường tròn ngoại tiếp trùng với tâm đường tròn nội tiếp và được gọi là tâm của đa giác đều.

3. Công thức tính bán kính đường tròn ngoại tiếp và đường tròn nội tiếp đa giác đều.

Đa giác đều n cạnh có độ dài mỗi cạnh là a, R là bán kính đường tròn ngoại tiếp và r là bán kính đường tròn nội tiếp đa giác. Ta có:

Giải bài tập đường tròn ngoại tiếp, đường tròn nội tiếp Toán 9 tập 2 phần hình học trang 91,92

Bài 61.a) Vẽ đường tròn tâm O, bán kính 2cm.

b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a)

c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O;r)

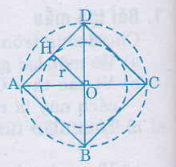
a) Chọn điểm O làm tâm , mở compa có độ dài 2cm vẽ đường tròn tâm O, bán kính 2cm: (O; 2cm)

Vẽ bằng eke và thước thẳng.

b) Vẽ đường kính AC và BD vuông góc với nhau. Nối A với B, B với C, C với D, D với A ta được tứ giác ABCD là hình vuông nội tiếp đường tròn (O;2cm)

c) Vẽ OH ⊥ AD

OH là bán kính r của đường tròn nội tiếp hình vuông ABCD.

r = OH = AH.

r² + r² = OA² = 2² => 2r² = 4 => r = √2  (cm)

Vẽ đường tròn (O;√2cm). Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh.

---

Bài 62. a) Vẽ tam giác ABC cạnh a = 3cm.

b) Vẽ đường tròn (O;R) ngoại tiếp tam giác đều ABC. Tính R.

c) Vẽ đường tròn (O;r) nội tiếp tam giác đều ABC. Tính r.

d) Vẽ tiếp tam giác đều IJK ngoại tiếp đường tròn (O;R).

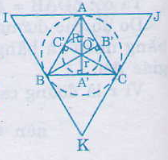
a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước có chia khoảng và compa)

b) Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác của tam giác đều ABC).

Ta có:  R= OA = 2/3AA’ = 2/3. AB√3/2 = 2/3.3√3 /2 = √3v(cm).

c) Đường tròn nội tiếp (O;r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A’, B’, C’ của các cạnh.

r = OA’ = 1/3AA’ =1/3. 3√3/2 =√3/2 (cm)

d) Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ∆IJK là tam giác đều ngoại tiếp (O;R).

---

Bài 63 trang 92 Toán 9 tập 2 – Hình học

Vẽ các hình lục giác đều, hình vuông, hình tam giác đều cùng nội tiếp đường tròn (O;R) rồi tính cạnh của các hình đó theo R.

Giải: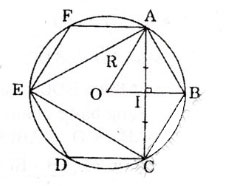

a) Vẽ lục giác đều ABCDEF nội tiếp đường tròn (O;R)

– Lấy điểm A tùy ý trên (O), vẽ cung tròn (A:R) cắt O tại B, vẽ tiêp cung tròn (B;R) cắt (O) tại C, tiếp tục làm như vậy ta sẽ chia đường tròn (O) thành 6 cung bằng nhau.

– Nối A với B, B với C… F với A. Hình ABCDEF là lục giác đều nội tiếp đường tròn (O).

* Tính cạnh của lục giác đều:

ABCDEF là lục giác đều ⇒  AB = BC = CD = DE = EF = FA

⇒sđ cung AB = 360⁰/5 = 600 ⇒  ∠AOB = 60⁰ ⇒ ΔAOB đều.

Vậy cạnh của lục giác đều bằng R.

b) Vẽ hình vuông nội tiếp (O,R) và tnh cạnh hình vuông (Xem bài 61).

c) Vẽ tam giác đều nội tiếp (O;R)

Ta vẽ như đã vẽ lục giác đều (Câu a). Sau khi chia (O) thành 6 phần bằng nhau, thay vì nối A với B thì ta nối A với C, C với E, F với A, ta sẽ được ΔACE và tam giác đều nội tiếp (O;R). Tính cạnh của tam giác đều ACE theo R.

Ta có: cung AB = BC ⇒ IA = IC ( I là giao điểm của BC với ON) (1) ⇒ OI ⊥ AC

ΔOIA vuông tại I và ∠AOB = 60⁰ (cmt)

⇒  AI = OA.sin∠O = R.sinh60⁰ = R.√3/2

(1)  ⇒  AC =2AI =2.(RR.√3/2) = R√3

Vậy cạnh của tam giác đều nội tiếp đường tròn  (O;R) bằng R√3

---

Bài 64. Trên đường tròn bán kính R lần lượt đặt theo cùng một chiều, kể từ điểm A, ba cung AB, BC, CD sao cho sđAB = 60^o, sđBC = 90^o và sđCD = 120^o

a) Tứ giác ABCD là hình gì?

b) Chứng minh hai đường chéo của tứ giác ABCD vuông góc với nhau.

c) Tính độ dài các cạnh của tứ giác ABCD theo R.

Giải. a) sđAD= 360⁰ -sđ(AB + BC +CD) = 90⁰

⇒ sđAD = sđBC = 90⁰ ⇒ cungAD = cungBC

⇒ ∠ABD = ∠BDC (Góc nội tiếp chắn hai cung bằng nhau)

⇒  AB//CD ⇒ ABCD là hình thang. (1)

Ta lại có:

⇒ AC = BD  (2) (hai dây căng hai cung bằng nhau)

Từ (1) và (2) ABCD là hình thang cân

b) Gọi I là giao điểm của AC và BD, ta có:

∠AIB =1/2sđ(cung AB + CD) = 1/2 (60⁰ +120⁰) ⇒ 90⁰ ⇒ AC ⊥ BD.

c) AB là cạnh của lục giác đều nội tiếp (O;R) ⇒ AB = R

BC và AD (căng cung có số đo 90⁰) là cạnh của hình vuông nội tiếp đường tròn (O;R) ⇒ BC = AD = R√2

CD (căng cung có số đo là 120⁰) là cạnh của tam giác đều nội tiếp đường tròn (O;R) ⇒ CD =R√3.