Bài 3 Toán 8: Giải bài 10 trang 12; bài 11,12,13 trang 13 SGK Toán 8 tập 2: Phương trình đưa được về dạng ax + b = 0.
– Để giải các phương trình đưa được về ax + b = 0 ta thường biến đổi phương trình như sau:
+ Quy đồng mẫu hai vế và khử mẫu.
+ Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng ax = c
+ Tìm x
Chú ý: Quá trình biến đổi phương trình về dạng ax = c có thể dẫn đến trường hợp đặc biệt là hệ số của ẩn bằng 0 nếu:
0x = c thì phương trình vô nghiệm S = Φ.
0x = 0 thì phương trình nghiệm đúng với mọi x hay vô số nghiệm: S = R.
Đáp án bài tập: Phương trình đưa được về dạng ax + b = 0 trang 12,13 SGK.
Bài 10. Tìm chỗ sai và sửa l
ại các bài giải sau cho đúng:
a) 3x – 6 + x = 9 – x b) 2t – 3 + 5t = 4t + 12
⇔ 3x + x – x = 9 – 6 ⇔ 2t + 5t – 4t = 12 -3
⇔ 3x = 3 ⇔ 3t = 9
⇔ x = 1 ⇔ t = 3.
Giải: a) Sai ở phương trình thứ hai chuyển vế hạng tử -6 từ vế trái sang vế phải, hạng tử -x từ vế phải sang vế trái mà không đổi dấu.
Giải lại: 3x – 6 + x = 9 – x
⇔ 3x + x + x = 9 + 6
⇔ 5x = 15
⇔ x = 3
Vậy phương trình có nghiệm duy nhất x = 3
b) Sai ở phương trình thứ hai, chuyển vế hạng tử -3 từ vế trái sang vế phải mà không đổi dấu.
Giải lại: 2t – 3 + 5t = 4t + 12
⇔ 2t + 5t – 4t = 12 + 3
⇔ 3t = 15
⇔ t = 5
Vậy phương trình có nghiệm duy nhất t = 5
Bài 11. Giải các phương trình:
a) 3x – 2 = 2x – 3; b) 3 – 4u + 24 + 6u = u + 27 + 3u;
c) 5 – (x – 6) = 4(3 – 2x); d) -6(1,5 – 2x) = 3(-15 + 2x);
e) 0,1 – 2(0,5t – 0,1) = 2(t – 2,5) – 0,7
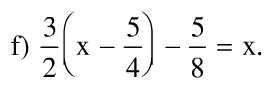
Advertisements (Quảng cáo)
Đáp án: a) 3x – 2 = 2x – 3
⇔ 3x – 2x = -3 + 2
⇔ x = -1
Vậy phương trình có nghiệm duy nhất x = -1.
b) 3 – 4u + 24 + 6u = u + 27 + 3u
⇔ 2u + 27 = 4u + 27
⇔ 2u – 4u = 27 – 27
⇔ -2u = 0
⇔ u = 0
Vậy phương trình có nghiệm duy nhất u = 0.
c) 5 – (x – 6) = 4(3 – 2x)
⇔ 5 – x + 6 = 12 – 8x
⇔ -x + 11 = 12 – 8x
⇔ -x + 8x = 12 – 11
⇔ 7x = 1
⇔ x = 1/7
Vậy phương trình có nghiệm duy nhất x = 1/7
d) -6(1,5 – 2x) = 3(-15 + 2x)
⇔ -9 + 12x = -45 + 6x
⇔ 12x – 6x = -45 + 9
Advertisements (Quảng cáo)
⇔ 6x = -36
⇔ x = -6
Vậy phương trình có nghiệm duy nhất x = -6
e) 0,1 – 2(0,5t – 0,1) = 2(t – 2,5) – 0,7
⇔ 0,1 – t + 0,2 = 2t – 5 – 0,7
⇔ -t + 0,3 = 2t – 5,7
⇔ -t – 2t = -5,7 – 0,3
⇔ -3t = -6
⇔ t = 2
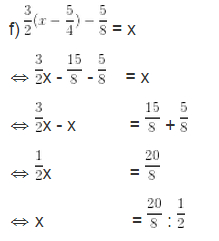
⇔ x = 5
Bài 12 trang 13 Giải các phương trình:

Đáp án :

⇔ 2(5x – 2) = 3(5 – 3x)
⇔ 10x – 4 = 15 – 9x
⇔ 10x + 9x = 15 + 4
⇔ 19x = 19
⇔ x = 1
![]()
![]()
⇔ 30x + 9 = 36 + 24 + 32x
⇔ 30x – 32x = 60 – 9
⇔ -2x = 51
⇔ x = -51/2 = -25,5
Vậy phương trình có nghiệm duy nhất x = -25,5.
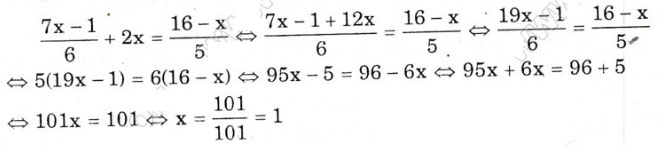
⇔ 2 – 6x = ![]()
⇔ 6 – 18x = -5x + 6
⇔ -18x + 5x = 0
⇔ -13x = 0
⇔ x = 0
Vậy phương trình có nghiệm duy nhất x = 0.
Bài 13. Bạn Hoà giải phương trình x(x + 2) = x(x + 3) như hình 2.
Theo em bạn Hoà giải đúng hay sai?
Em sẽ giải phương trình đó như thế nào?

Bạn Hoà đã giải sai.
Không thể chia hai vế của phương trình đã cho với x để được phương trình
x + 2 = x + 3.
Lời giải đúng: x(x + 2) = x(x + 3)
⇔ x2 + 2x = x2 + 3x
⇔ x2 + 2x – x2 – 3x = 0
⇔ -x = 0
⇔ x = 0
Vậy phương trình đã cho có nghiệm là x = 0




![[THCS Trần Cao] thi môn Toán lớp 8 cuối học kì 2: Mẫu số của một phân số lớn hơn tử số của nó là 5, nếu tăng cả tử lẫn mẫu của nó thêm 5 đơn vị thì được phân số mới bằng phân số 2 /3. Tìm phân số ban đầu](https://dethikiemtra.com/wp-content/uploads/2020/09/anh-chup-dep-ve-gia-dinh_035107328-100x75.jpg)
