
Cho hình thoi ABCD có \(\widehat A = {60^ \circ }\). Gọi E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA. Chứng minh rằng EBFGDH là lục giác đều.

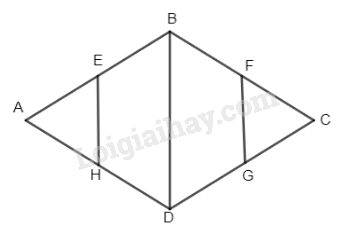
\(\Delta ABD\) cân (AB = AD) có \(\widehat A = {60^ \circ }\) (gt) nên \(\Delta ABD\) đều
\( \Rightarrow AB = BC = CD = AD = BD\) và EH, FG lần lượt là các đường trung bình của \(\Delta ABD\) và \(\Delta CBD.\)
Advertisements (Quảng cáo)
Ta có: \(EH = FG = \dfrac{1 }{2}BD\)
Lại có E, F, G, H là các trung điểm của AB, BC, CD, DE nên EB = BF = FG = GD = DH = HE (1)
Mặt khác \(\widehat {AEH} = {60^ \circ }(\Delta AEH (đều) \) \(\Rightarrow \widehat {BEH} = {120^ \circ }\) (kề bù)
Tương tự ta chứng minh được \(\widehat {BFG} = \widehat {DGF} = \widehat {DHE} = {120^ \circ }\)
Advertisements (Quảng cáo)
Hiển nhiên \(\widehat {ABC} = \widehat {ADC} = {120^ \circ }\) (vì \(\widehat A = {60^ \circ }\))
\( \Rightarrow \widehat {BFG} = \widehat {DGF} = \widehat {HDE} = \widehat {EBF}\)\(\, = \widehat {HDG} = {120^ \circ }\) (2)
Từ (1) và (2) \( \Rightarrow EBFGDH\) là lục giác đều.

![[Có đáp án 2018] Đề thi học kì Toán lớp 8 trường Bằng Lang trắc nghiệm và tự luận](https://dethikiemtra.com/wp-content/uploads/2018/04/dap-an-cau-4-100x75.jpg)




