Cho hình vuông ABCD có cạnh a, giao điểm hai đường chéo là O. Một góc vuông \(\widehat {xOy}\) sao cho Ox cắt cạnh AB tại E, tia Oy cắt cạnh BC tại F … trong Đề kiểm tra 15 phút môn Toán học Chương 2 Hình học 8. Xem Đề và đáp án đầy đủ phía dưới đây

Cho hình vuông ABCD có cạnh a, giao điểm hai đường chéo là O. Một góc vuông \(\widehat {xOy}\) sao cho Ox cắt cạnh AB tại E, tia Oy cắt cạnh BC tại F.
Tính \({S_{OEBF}}\) theo a.

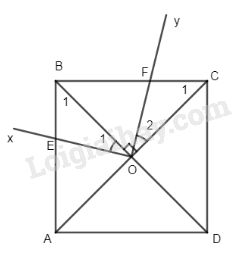
Ta có: \({S_{OEBF}} = {S_{OEB}} + {S_{OFB}}.\)
Advertisements (Quảng cáo)
Nối O với A, B. Xét \(\Delta OEB\) và a\(\Delta OFC\)có:
\(\widehat {{B_1}} = \widehat {{C_1}} = {45^ \circ },\)
OB = OC,
Advertisements (Quảng cáo)
\(\widehat {{O_1}} = \widehat {{O_2}}\) (cùng phụ với \(\widehat {{\rm{BOF}}}\)).
\( \Rightarrow \Delta OEB = \Delta OFC\left( {g.c.g} \right)\)
Do đó: \({S_{OEBF}} = {S_{OFC}} + {S_{OFB}} = {S_{OBC}} \)\(\,=\dfrac {1}{ 4}{S_{ABCD}} = {1 \over 4}{a^2}.\)






