
1. Trong không gian \(Oxyz\) cho ba vectơ \(\overrightarrow a = \left( {3; – 2;4} \right),\)\(\mathop b\limits^ \to = \left( {5;1;6} \right)\), \(\mathop c\limits^ \to = \left( { – 3;0;2} \right)\). Tìm vectơ \(\overrightarrow x \) sao cho vectơ \(\overrightarrow x \) đồng thời vuông góc với \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \)
A. \(\left( {1;0;0} \right).\) B. \(\left( {0;0;1} \right).\)
C. \(\left( {0;1;0} \right).\) D. \(\left( {0;0;0} \right).\)
2. Trong không gian\(Oxyz\), cho 2 điểm \(B(1;2; – 3)\),\(C(7;4; – 2)\). Nếu \(E\) là điểm thỏa mãn đẳng thức \(\overrightarrow {CE} = 2\overrightarrow {EB} \) thì tọa độ điểm \(E\) là
A. \(\left( {3;\dfrac{8}{3}; – \dfrac{8}{3}} \right).\) B. \(\left( {3;\dfrac{8}{3};\dfrac{8}{3}} \right).\) C. \(\left( {3;3; – \dfrac{8}{3}} \right).\) D. \(\left( {1;2;\dfrac{1}{3}} \right).\)
3. Trong không gian với hệ trục tọa độ \(Oxyz\), cho ba điểm \(A(1;2; – 1)\), \(B(2; – 1;3)\),\(C( – 2;3;3)\). Điểm\(M\left( {a;b;c} \right)\) là đỉnh thứ tư của hình bình hành \(ABCM\), khi đó \(P = {a^2} + {b^2} – {c^2}\) có giá trị bằng
A.\(43.\). B. \(44.\).
C. \(42.\). D. \(45.\)
4. Trong không gian với hệ trục tọa độ \(Oxyz\)cho ba điểm \(A(1;2; – 1)\), \(B(2; – 1;3)\),\(C( – 2;3;3)\). Tìm tọa độ điểm\(D\) là chân đường phân giác trong góc \(A\) của tam giác\(ABC\)
A. \(D(0;1;3)\). B. \(D(0;3;1)\). C. \(D(0; – 3;1)\). D. \(D(0;3; – 1)\).
5. Trong không gian với hệ toạ độ \(Oxyz\), cho các điểm: A(-1,3,5), B(-4,3,2), C(0,2,1). Tìm tọa độ điểm \(I\) tâm đường tròn ngoại tiếp tam giác \(ABC\)
A. \(I(\dfrac{8}{3};\dfrac{5}{3};\dfrac{8}{3})\). B. \(I(\dfrac{5}{3};\dfrac{8}{3};\dfrac{8}{3})\).
C. \(I( – \dfrac{5}{3};\dfrac{8}{3};\dfrac{8}{3}).\) D. \(I(\dfrac{8}{3};\dfrac{8}{3};\dfrac{5}{3})\).
6. Trong không gian \(Oxyz\), cho 3 vectơ 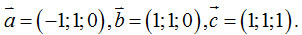 . Cho hình hộp \(OABC.O’A’B’C’\) thỏa mãn điều kiện
. Cho hình hộp \(OABC.O’A’B’C’\) thỏa mãn điều kiện 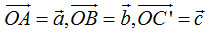 . Thể tích của hình hộp nói trên bằng:
. Thể tích của hình hộp nói trên bằng:
A. \(\dfrac{1}{3}\) B. 4
C. \(\dfrac{2}{3}\) D. 2
7. Trong không gian với hệ trục \(Oxyz\) cho tọa độ 4 điểm A(2;-1;1), B(1;0;0), C(3,1,0), D(0;2;1). Cho các mệnh đề sau:
1) Độ dài \(AB = \sqrt 2 \).
2) Tam giác \(BCD\) vuông tại \(B\).
3) Thể tích của tứ diện \(ABCD\) bằng \(6\).
Các mệnh đề đúng là:
A. 2). B. 3).
C. 1); 3). D. 2), 1)
8. Trong không gian\(Oxyz\), cho ba vectơ \(\overrightarrow a = \left( { – 1,1,0} \right);\overrightarrow b = (1,1,0);\overrightarrow c = \left( {1,1,1} \right)\). Trong các mệnh đề sau, mệnh đề nào đúng:
A. \(\cos \left( {\overrightarrow b ,\overrightarrow c } \right) = \dfrac{{\sqrt 6 }}{3}.\)
B. \(\overrightarrow a + \overrightarrow b + \overrightarrow c = \overrightarrow 0 .\)
A. \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng.
D. \(\overrightarrow a .\overrightarrow b = 1.\)
9. Trong không gian với hệ tọa độ \(Oxyz\), cho tứ diện \(ABCD\), biết \(A(1;0;1)\),\(B( – 1;1;2)\), \(C( – 1;1;0)\), \(D(2; – 1; – 2)\). Độ dài đường cao \(AH\)của tứ diện \(ABCD\) bằng:
A. \(\dfrac{2}{{\sqrt {13} }}.\) B. \(\dfrac{1}{{\sqrt {13} }}.\)
C. \(\dfrac{{\sqrt {13} }}{2}.\) D. \(\dfrac{{3\sqrt {13} }}{{13}}.\)
10: Cho hình chóp tam giác \(S.ABC\) với \(I\) là trọng tâm của đáy \(ABC\). Đẳng thức nào sau đây là đẳng thức đúng
A. \(\overrightarrow {SI} = \dfrac{1}{2}\left( {\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} } \right).\)
B. \(\overrightarrow {SI} = \dfrac{1}{3}\left( {\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} } \right).\)
C. \(\overrightarrow {SI} = \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} .\)
D. \(\overrightarrow {SI} + \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = \overrightarrow 0 .\)
11: Phương trình mặt cầu tâm \(I\left( {2;4;6} \right)\) nào sau đây tiếp xúc với trục Ox:
A. \({\left( {x – 2} \right)^2} + {\left( {y – 4} \right)^2} + {\left( {z – 6} \right)^2} = 20.\)
B. \({\left( {x – 2} \right)^2} + {\left( {y – 4} \right)^2} + {\left( {z – 6} \right)^2} = 40.\)
C. \({\left( {x – 2} \right)^2} + {\left( {y – 4} \right)^2} + {\left( {z – 6} \right)^2} = 52.\)
D. \({\left( {x – 2} \right)^2} + {\left( {y – 4} \right)^2} + {\left( {z – 6} \right)^2} = 56.\)
12: Mặt cầu tâm \(I\left( {2;4;6} \right)\) tiếp xúc với trục Oz có phương trình:
A. \({\left( {x – 2} \right)^2} + {\left( {y – 4} \right)^2} + {\left( {z – 6} \right)^2} = 20.\)
B. \({\left( {x – 2} \right)^2} + {\left( {y – 4} \right)^2} + {\left( {z – 6} \right)^2} = 40.\)
Advertisements (Quảng cáo)
C. \({\left( {x – 2} \right)^2} + {\left( {y – 4} \right)^2} + {\left( {z – 6} \right)^2} = 52.\)
D. \({\left( {x – 2} \right)^2} + {\left( {y – 4} \right)^2} + {\left( {z – 6} \right)^2} = 56.\)
13: Cho mặt cầu \(\left( S \right)\): \({\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} + {\left( {z – 3} \right)^2} = 9\). Phương trình mặt cầu nào sau đây là phương trình của mặt cầu đối xứng với mặt cầu (S) qua mặt phẳng (Oxy):
A. \({\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z + 3} \right)^2} = 9.\)
B. \({\left( {x + 1} \right)^2} + {\left( {y – 2} \right)^2} + {\left( {z + 3} \right)^2} = 9.\)
C. \({\left( {x – 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z + 3} \right)^2} = 9.\)
D. \({\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} + {\left( {z + 3} \right)^2} = 9.\)
14: Cho mặt cầu \(\left( S \right)\): \({\left( {x + 1} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z – 2} \right)^2} = 4\). Phương trình mặt cầu nào sau đây là phương trình mặt cầu đối xứng với mặt cầu (S) qua trục Oz:
A. \({\left( {x – 1} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z – 2} \right)^2} = 4.\)
B. \({\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z – 2} \right)^2} = 4.\)
C. \({\left( {x – 1} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z – 2} \right)^2} = 4.\)
D. \({\left( {x + 1} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z + 2} \right)^2} = 4.\)
15: Đường tròn giao tuyến của \(\left( S \right):{\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} + {\left( {z – 3} \right)^2} = 16\) khi cắt bởi mặt phẳng (Oxy) có chu vi bằng:
A. \(\sqrt 7 \pi .\) B. \(2\sqrt 7 \pi .\)
C. \(7\pi .\) D. \(14\pi .\)
16: Trong không gian với hệ toạ độ \(Oxyz\),tọa độ điểm \(M\) nằm trên trục \(Oy\) và cách đều hai mặt phẳng: \(\left( P \right):x + y – z + 1 = 0\) và \(\left( Q \right):x – y + z – 5 = 0\) là:
A.\(M\left( {0; – 3;0} \right)\). B.\(M\left( {0;3;0} \right)\).
C.\(M\left( {0; – 2;0} \right)\). D. \(M\left( {0;1;0} \right)\).
17: Trong không gian với hệ toạ độ \(Oxyz\), gọi \(\left( \alpha \right)\) là mặt phẳng qua \(G\left( {1;2;3} \right)\) và cắt các trục \(Ox,Oy,Oz\) lần lượt tại các điểm \(A,B,C\) (khác gốc \(O\)) sao cho \(G\) là trọng tâm của tam giác \(ABC\). Khi đó mặt phẳng \(\left( \alpha \right)\) có phương trình:
A.\(3x + 6y + 2z + 18 = 0\).
B.\(6x + 3y + 2z – 18 = 0\).
C.\(2x + y + 3z – 9 = 0\).
D.\(6x + 3y + 2z + 9 = 0\).
18: Trong không gian với hệ toạ độ \(Oxyz\), gọi \(\left( \alpha \right)\)là mặt phẳng song song với mặt phẳng \(\left( \beta \right):2x – 4y + 4z + 3 = 0\) và cách điểm \(A\left( {2; – 3;4} \right)\) một khoảng \(k = 3\). Phương trình của mặt phẳng \(\left( \alpha \right)\) là:
A.\(2x – 4y + 4z – 5 = 0\) hoặc \(2x – 4y + 4z – 13 = 0\).
B. \(x – 2y + 2z – 25 = 0\).
C.\(x – 2y + 2z – 7 = 0\).
D.\(x – 2y + 2z – 25 = 0\) hoặc \(x – 2y + 2z – 7 = 0\).
19: Trong không gian với hệ toạ độ \(Oxyz\),cho hai đường thẳng \({d_1},{d_2}\)lần lượt có phương trình \({d_1}:\dfrac{{x – 2}}{2} = \dfrac{{y – 2}}{1} = \dfrac{{z – 3}}{3}\), \({d_2}:\dfrac{{x – 1}}{2} = \dfrac{{y – 2}}{{ – 1}} = \dfrac{{z – 1}}{4}\). Phương trình mặt phẳng \(\left( \alpha \right)\) cách đều hai đường thẳng \({d_1},{d_2}\) là:
A.\(7x – 2y – 4z = 0\).
Advertisements (Quảng cáo)
B.\(7x – 2y – 4z + 3 = 0\).
C. \(2x + y + 3z + 3 = 0\).
D.\(14x – 4y – 8z + 3 = 0\).
20: Trong không gian \({\left( {x + 4} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z + 6} \right)^2} = 18.\), cho mặt phẳng \({\left( {x – 4} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z – 6} \right)^2} = 9.\): \({\left( {x – 4} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z – 6} \right)^2} = 16.\) và đường thẳng \(d\):\(N( – 5;7;0)\). Với giá trị nào của \(\vec u = (2; – 2;1)\)thì \(\overrightarrow {MN} = ( – 9;6; – 6)\)cắt \(H\)
A.\(\left( S \right)\).
B.\(\left( S \right)\) .
C.\({R^2} = M{H^2} + {\left( {\dfrac{{AB}}{2}} \right)^2} = 18\) .
D.\(d(M,d) = 3\).

|
Câu |
1 |
2 |
3 |
4 |
5 |
|
Đáp án |
D |
A |
B |
A |
C |
|
Câu |
6 |
7 |
8 |
9 |
10 |
|
Đáp án |
D |
A |
A |
B |
B |
|
Câu |
11 |
12 |
13 |
14 |
15 |
|
Đáp án |
C |
A |
D |
A |
B |
|
Câu |
16 |
17 |
18 |
19 |
20 |
|
Đáp án |
A |
B |
D |
D |
D |
1. Dễ thấy chỉ có \(\overrightarrow x = (0;0;0)\)thỏa mãn \(\overrightarrow x .\overrightarrow a = \overrightarrow x .\overrightarrow b = \overrightarrow x .\overrightarrow c = 0.\)
2. \(E(x;y;z)\), từ \(\overrightarrow {CE} = 2\overrightarrow {EB} \Rightarrow \left\{ \begin{array}{l}x = 3\\y = \dfrac{8}{3}\\z = – \dfrac{8}{3}\end{array} \right..\)
3. \(M(x;y;z)\), \(ABCM\) là hình bình hành thì
\(\overrightarrow {AM} = \overrightarrow {BC} \Rightarrow \left\{ \begin{array}{l}x – 1 = – 2 – 2\\y – 2 = 3 + 1\\z + 1 = 3 – 3\end{array} \right.\)
\(\Rightarrow M( – 3;6; – 1) \Rightarrow P = 44.\).
4. Ta có \(AB = \sqrt {26} ,AC = \sqrt {26} \Rightarrow \) tam giác \(ABC\)cân ở \(A\) nên \(D\) là trung điểm \(BC\) \( \Rightarrow D(0;1;3).\)
5. Ta có: Tam giác đều. Do đó tâm \(I\) của đường tròn ngoại tiếp là trọng tâm của nó. Kết luận: \(I\left( { – \dfrac{5}{3};\dfrac{8}{3};\dfrac{8}{3}} \right)\)
6. \(\begin{array}{l}
\overrightarrow {OA} = \overrightarrow a \Rightarrow A\left( { – 1;1;0} \right),\\
\overrightarrow {OB} = \overrightarrow b \Rightarrow B\left( {1;1;0} \right),\\
\overrightarrow {OC’} = \overrightarrow c \Rightarrow C’\left( {1;1;1} \right).
\end{array}\)
\(\overrightarrow {AB} = \overrightarrow {OC} \Rightarrow C(2;0;0)\)\( \Rightarrow \overrightarrow {CC’} = ( – 1;1;1) = \overrightarrow {OO’} \) \( \Rightarrow {V_{OABC.O’A’B’C’}} = \left| {\left[ {\overrightarrow {OA} ,\overrightarrow {OB} } \right]\overrightarrow {OO’} } \right|\)
8. \(\cos (\overrightarrow b ,\overrightarrow c ) = \dfrac{{\overrightarrow b .\overrightarrow c }}{{\left| {\overrightarrow b } \right|.\left| {\overrightarrow c } \right|}}\)
9. Sử dụng công thức \(h = \dfrac{{\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AD} } \right|}}{{\left| {\overrightarrow {AB} .\overrightarrow {AC} } \right|}} = \dfrac{1}{{\sqrt {13} }}.\)
10: \(\left. \begin{array}{l}\overrightarrow {SI} = \overrightarrow {SA} + \overrightarrow {AI} \\\overrightarrow {SI} = \overrightarrow {SB} + \overrightarrow {BI} \\\overrightarrow {SI} = \overrightarrow {SC} + \overrightarrow {CI} \end{array} \right\}\\ \Rightarrow 3\overrightarrow {SI} = \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SB} + \left( {\overrightarrow {AI} + \overrightarrow {BI} + \overrightarrow {CI} } \right)\)
Vì I là trọng tâm tam giác \(ABC \Rightarrow \overrightarrow {AI} + \overrightarrow {BI} + \overrightarrow {CI} = \overrightarrow 0 \)
\(\Rightarrow \overrightarrow {SI} = \dfrac{1}{3}\left( {\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} } \right).\)
11: Mặt cầu tâm \(I\left( {2;4;6} \right)\), bán kính R và tiếp xúc trục Ox\( \Leftrightarrow R = d\left( {I;Ox} \right)\)
\( \Leftrightarrow R = \sqrt {y_I^2 + z_I^2} = \sqrt {52} \). Vậy \(\left( S \right):{\left( {x – 2} \right)^2} + {\left( {y – 4} \right)^2} + {\left( {z – 6} \right)^2} = 52.\)
Lựa chọn đáp án C.
12: Mặt cầu tâm \(I\left( {2;4;6} \right)\), bán kính R và tiếp xúc trục Ox\( \Leftrightarrow R = d\left( {I;Oz} \right)\)
\( \Leftrightarrow R = \sqrt {x_I^2 + y_I^2} = \sqrt {20} \). Vậy \(\left( S \right):{\left( {x – 2} \right)^2} + {\left( {y – 4} \right)^2} + {\left( {z – 6} \right)^2} = 20.\)
Lựa chọn đáp án A.
13: Mặt cầu \(\left( S \right)\) tâm \(I\left( {1;2;3} \right)\), bán kính \(R = 3\). Do mặt cầu \(\left( {S’} \right)\) đối xứng với \(\left( S \right)\) qua mặt phẳng (Oxy) nên tâm I’ của \(\left( {S’} \right)\) đối xứng với I qua (Oxy), bán kính \(R’ = R = 3\).
Ta có : \(I’\left( {1;2; – 3} \right)\). Vậy \(\left( S \right):{\left( {x – 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z – 3} \right)^2} = 9.\)
Lựa chọn đáp án D.
Lưu ý: Để ý thấy rằng trung điểm \(II’\) thuộc mặt phẳng \(\left( {Oxy} \right)\) và \(\overrightarrow {II’} \bot \left( {Oxy} \right)\). Cả 4 đáp án trên đều có thể dễ dàng tìm được tọa độ \(I’\) nên nếu tinh ý ta sẽ tiết kiệm được thời gian hơn trong việc tìm đáp án.
14: Mặt cầu \(\left( S \right)\) tâm \(I\left( { – 1;1;2} \right)\), bán kính \(R = 2\). Do mặt cầu \(\left( {S’} \right)\) đối xứng với \(\left( S \right)\) qua trục Oz nên tâm I’ của \(\left( {S’} \right)\) đối xứng với I qua trục Oz, bán kính \(R’ = R = 2\).
Ta có : \(I’\left( {1; – 1;2} \right)\). Vậy \(\left( S \right):{\left( {x – 1} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z – 2} \right)^2} = 4.\)
Lựa chọn đáp án A.
15: Mặt cầu \(\left( S \right)\) tâm \(I\left( {1;2;3} \right)\), bán kính \(R = 4\). Ta có : \(d\left( {I;\left( {Oxy} \right)} \right) = \left| {{z_I}} \right| = 3\).
Gọi \(r\) là bán kính đường tròn (C) giao tuyến của mặt cầu \(\left( S \right)\) và mặt phẳng (Oxy), ta suy ra :
\(r = \sqrt {{R^2} – {{\left[ {d\left( {I;\left( {Oxy} \right)} \right)} \right]}^2}} = \sqrt 7 \). Vậy chu vi (C) bằng : \(2\sqrt 7 \pi \).
Lựa chọn đáp án B.
16: Ta có \(M \in Oy \Rightarrow M\left( {0;m;0} \right)\)
Giả thiết có \(d\left( {M,\left( P \right)} \right) = d\left( {M,\left( Q \right)} \right)\)\( \Leftrightarrow \dfrac{{\left| {m + 1} \right|}}{{\sqrt 3 }} = \dfrac{{\left| { – m – 5} \right|}}{{\sqrt 3 }}\)\( \Leftrightarrow m = – 3\)
Vậy \(M\left( {0; – 3;0} \right)\)
17: Gọi , , là giao điểm của mặt phẳng các trục
Phương trình mặt phẳng \(\left( \alpha \right)\) :\(\dfrac{x}{a} + \dfrac{y}{b} + \dfrac{z}{c} = 1\) \(\left( {a,b,c \ne 0} \right)\) .
Ta có \(G\) là trọng tâm tam giác \(ABC\) \( \Rightarrow \left\{ \begin{array}{l}\dfrac{a}{3} = 1\\\dfrac{b}{3} = 2\\\dfrac{c}{3} = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = 6\\c = 9\end{array} \right.\)\( \Rightarrow \left( \alpha \right):\dfrac{x}{3} + \dfrac{y}{6} + \dfrac{z}{9} = 1 \Leftrightarrow 6x + 3y + 2z – 18 = 0\)
18: Vì \(\left( \alpha \right)//\left( \beta \right)\)\( \Rightarrow \left( \alpha \right):2x – 4y + 4z + m = 0\)\(\left( {m \ne 3} \right)\)
Giả thiết có \(d\left( {A,\left( \alpha \right)} \right) = 3\)\( \Leftrightarrow \dfrac{{\left| {32 + m} \right|}}{6} = 3\)\( \Leftrightarrow \left[ \begin{array}{l}m = – 14\\m = – 50\end{array} \right.\)
Vậy \(\left( \alpha \right):x – 2y + 2z – 7 = 0\), \(\left( \alpha \right):x – 2y + 2z – 25 = 0\)
19: Ta có \({d_1}\) đi qua \(A\left( {2;2;3} \right)\) và có \(\overrightarrow {{u_{{d_1}}}} = \left( {2;1;3} \right)\), \({d_2}\) đi qua \(B\left( {1;2;1} \right)\) và có \(\overrightarrow {{u_{{d_2}}}} = \left( {2; – 1;4} \right)\)
\(\overrightarrow {AB}= \left( { – 1;1; – 2} \right);\left[ {\overrightarrow {{u_{{d_1}}}}; \overrightarrow {{u_{{d_2}}}} } \right] = \left( {7; – 2; – 4} \right)\)
\( \Rightarrow \left[ {\overrightarrow {{u_{{d_1}}}}; \)\(\overrightarrow {{u_{{d_2}}}}} \right]\overrightarrow {AB}= – 1 \ne 0\) nên \({d_1},{d_2}\) chéo nhau.
Do \(\left( \alpha \right)\) cách đều \({d_1},{d_2}\) nên \(\left( \alpha \right)\) song song với \({d_1},{d_2}\)\( \Rightarrow \overrightarrow {{n_\alpha }} = \left[ {\overrightarrow {{u_{{d_1}}}} ;\overrightarrow {{u_{{d_2}}}} } \right] = \left( {7; – 2; – 4} \right)\)
\( \Rightarrow \left( \alpha \right)\) có dạng \(7x – 2y – 4z + d = 0\)
Theo giả thiết thì \(d\left( {A,\left( \alpha \right)} \right) = d\left( {B,\left( \alpha \right)} \right)\)\( \Leftrightarrow \dfrac{{\left| {d – 2} \right|}}{{\sqrt {69} }} = \dfrac{{\left| {d – 1} \right|}}{{\sqrt {69} }} \Leftrightarrow d = \dfrac{3}{2}\)
\( \Rightarrow \left( \alpha \right):14x – 4y – 8z + 3 = 0\)
20:\({\left( {x – 4} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z – 6} \right)^2} = 18.\) có VTPT \(Oxyz\)
\({x^2} + {y^2} + {z^2} – 2x + 4y – 6z – 11 = 0\) có VTCP \((P)\)
\(2x + 2y – z – 7 = 0\)cắt \((Q)\)
Chọn đáp án D.






