Đề số 16 Thi học kì 1 môn Toán 6: Tìm tổng các số nguyên thỏa mãn -10 < x ≤ 8

Bài 1. Tìm tổng các số nguyên thỏa mãn -10 < x ≤ 8

Bài 2. Tìm x ∈ Z, biết 14 chia hết cho 2x + 3

Bài 3. Tìm x, biết 2 – x = – 15 – |-5|

Bài 4. Số học sinh khối 6 của một trường trung học cơ sỉ có khoảng từ 350 đến 400 em. Mỗi lần xếp hàng 3; hàng 4; hàng 5 đều vừa đủ. Hỏi khối 6 trường đó có bao nhiêu học sinh?

Bài 5. Tìm các số có dạng \(\overline {517xy} \) chia hết cho 18.

Bài 6. Cho đường thẳng d và hai điểm A và B nằm trên cùng một nửa mặt phẳng bờ d. Lấy điểm C không thuộc đường thẳng d nhưng đoạn BC cắt đường thẳng d. Hỏi đoạn AC có cắt đường thẳng d không?

Bài 7. Một điểm A nằm trên dường thẳng xy. Trên tia Ax lấy điếm B sao cho AB = 4cm, trên tia Ay lấy điểm C sao cho độ dài AC gấp đôi độ dài AB.

a) Tính độ dài đoạn thẳng BC.

b) Gọi E là trung điểm của AC, điểm A có phải là trung điểm của đoạn thẳng BE không? Vì sao?

Bài 1. x ∈ Z và -10 < x ≤ 8   ⇒ x ∈ {-9, -8, …, 7, 8}

Ta có: (-9) + (-8) + …+ 7 + 8 = (-9) + [(-8) + 8] + [(-7) + 7] + …+ [(-2) + 2] + [(-1) + 1] = -9

Bài 2. Tập các ước nguyên của 14 là : ±1, ±7, ± 14

Vậy ta có: 2x + 3 = 1 ⇒ x = -1; 2x + 3 = -1 ⇒ x = -2; 2x + 3 = 7

⇒ x = 2; 2x + 3 = -7 ⇒ x = -5; 2x + 3 = ± 14

(không thỏa mãn, vì x ∈ Z ⇒ 2x + 3  là số lẻ, còn 14 là số chẵn)

Bài 3. Ta có: 2 – x = – 14 – |5| ⇒ 2 – x  = -14 – 5 ⇒ 2 – x = -19

⇒ – x = -2 – 19 ⇒ x = 21

Bài 4. BCNN (3, 4, 5) = 60

Ta thấy trong khoảng từ 350 đến 400 có 360 là bội của 60

Vậy số học sinh cần tìm là 360 (em)

Bài 5. Vì \(\overline {517xy}  \vdots 2 \Rightarrow y = 0,2,4,6,8\)

+ Nếu y = 0, ta có: \(\overline {517×0}  \vdots 9 \Leftrightarrow (5 + 1 + 7 + x + 0) \vdots 9\)

Và x ∈ N, 0 ≤ x ≤ 9 ⇒ x = 5

Vậy x = 5, y = 0; ta có số 51750 ⋮ 18

+ Nếu y = 2, ta có: \(\overline {517×2}  \vdots 9\)

Tương tự, ta tìm được x = 3

Ta có: 51732 ⋮ 18

Tương tự, ta còn tìm được: 51714; 51786; 51768 chia hết cho 18.

Bài 6.

C không thuộc đường thẳng d, nhưng đoạn ĐC cắt đường thẳng d. Gọi M là giao điểm của đoạn BC và đường thẳng d ta có M nằm giữa hai điểm B và c, mà M thuộc d nên B và c nằm trên hai nửa một phẳng đối nhau bờ là đường thẳng d.

Ta lại có A và B nằm cùng trên một nửa mặt phẳng bờ d nên điểm A và C nằm trên hai nửa mặt phẳng đối nhau bờ d. Do đó đoạn AC cắt đường thẳng d.

Bài 7.

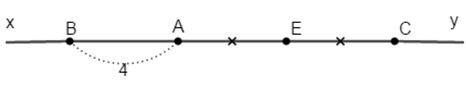
a) \(AC = 2AB = 2.4 = 8\; (cm).\)

Ta có A nằm trên đường thẳng xy nên Ax và Ay là hai tia đối nhau. Điểm B thuộc tia Ax, điểm C thuộc tia AC nên AB và AC là hai tia đối nhau. Do đó A là điểm nằm giữa B và C, ta có:

\(AB + AC = BC\) hay \(BC = 4 + 8 = 12\; (cm).\)

b) E là trung điểm cùa AC nên \(AE = CE = \dfrac{{AC}}{ 2} =\dfrac {8 }{ 2} = 4(cm)\)

Mặt khác vì E là trung điểm của AC nên AE và AC là hai tia trùng nhau. Mà AC và AB là hai tí đối nhau nên AE và AB cũng là hai tia đối nhau. Do đó A nằm giữa hai điểm B và E.

Lại có \(AB = AE = 4\; (cm)\). Vậy A là trung điểm của đoạn thẳng BE.