
Cho tam giác ABC, lấy các điểm D, E theo thứ tự trên các cạnh AB, AC sao cho BD = CE. Gọi M, N, I, K lần lượt là trung điểm của BE, CD, DE, BC. Chứng minh rằng: \(IK \bot MN.\)

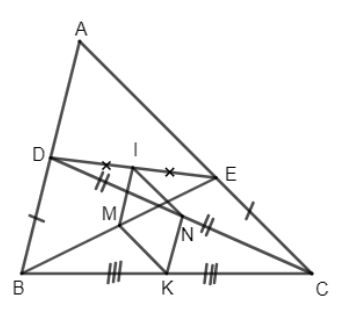
Ta có M là trung điểm của BE
I là trung điểm của DE
Advertisements (Quảng cáo)
\( \Rightarrow MI\) là đường trung bình của \(\Delta BDE\)
\( \Rightarrow MI//BD\) và \(MI = \dfrac{1}{2}BD\)
Tương tự \(NK//BD\) và \(NK = \dfrac{1}{2}BD\)
Advertisements (Quảng cáo)
Do đó \(MI//NK\) nên tứ giác MINK là hình bình hành (1)
Chứng minh tương tự ta có IN là đường trung bình của \(\Delta CDE\)
\( \Rightarrow IN = \dfrac{1 }{ 2}CE\) mà CE = BD (gt) \( \Rightarrow IN = IM\) (2)
Từ (1) và (2) \( \Rightarrow \) Tứ giác MINK là hình thoi (hình bình hành có hai cạnh kề bằng nhau)






