
Gọi O là giao điểm các đường chéo của hình bình hành ABCD. Chứng minh rằng giao điểm các đường phân giac trong của các tam giác AOB; BOC; COD và DOA là đỉnh của một hình thoi.

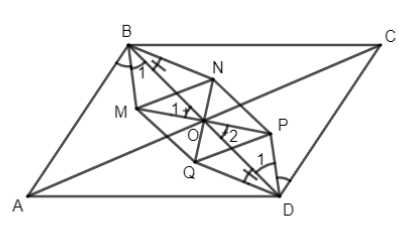
Gọi M, N, P, Q lần lượt là giao điểm các phân giác trong của các tam giác AOB, BOC, COD và DOA.
Advertisements (Quảng cáo)
Do O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD nên OA = OC và OB = OD.
Lại có: \(\widehat B_1 = \widehat D_1;\widehat O_1 = \widehat O_2\) (M là giao điểm của các đường phân giác)
\( \Rightarrow \Delta BMO = \Delta DPO\left( {g.c.g} \right)\)
Advertisements (Quảng cáo)
\(\Rightarrow OM = OP\)
Mặt khác ta có các điểm B, O, D thẳng hàng mà \(\widehat O_1 = \widehat O_2\) nên các điểm M, O, P cũng thẳng hàng. Tương tự ta có \(\Delta BON = \Delta DOQ \Rightarrow ON = OQ\) và N, O, Q cũng thẳng hàng \( \Rightarrow MNPQ\) là hình bình hành (các đường chéo cắt nhau tại trung điểm mỗi đường). Mặt khác OM, ON là hai phân giác của hai góc kề bù nên \(OM \bot ON.\) Vậy MNPQ là hình thoi.






