
Các đường phân giác trong của tứ giác ABCD tạo thành một tứ giác. Chứng minh rằng tứ giác đó có các góc đối bù nhau.

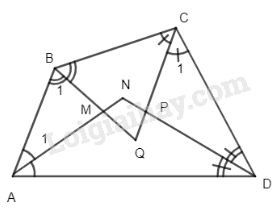
Gọi MNPQ là tứ giác được tạo thành, ta có :
\(\widehat A + \widehat Q + \widehat C + \widehat D = {360^ \circ }\)
Advertisements (Quảng cáo)
\( \Rightarrow {{\widehat A} \over 2} + {{\widehat B} \over 2} + {{\widehat C} \over 2} + {{\widehat D} \over 2} = {180^ \circ }.\)
Xét \(\Delta AMB\)có \(\widehat {{A_1}} + \widehat {AMB} + \widehat {{B_1}} = {180^ \circ }\)
Hay \({{\widehat A} \over 2} + \widehat {AMB} + \widehat {{B_1}} = {180^ \circ }.\)
Advertisements (Quảng cáo)
Tương tự với \(\Delta CPD:{{\widehat C} \over 2} + \widehat {CPD} + {{\widehat D} \over 2} = {180^ \circ }.\)
\( \Rightarrow \widehat {AMB} + \widehat {CPD} = {180^ \circ }\)
\(\Rightarrow \widehat {NMQ} + \widehat {NPQ} = {180^ \circ }\)
\( \Rightarrow \widehat {MNP} + \widehat {MQP} \)\(\,= {360^ \circ } – \left( {\widehat {NMQ} + \widehat {NPQ}} \right)\)\(\, = {360^ \circ } – {180^ \circ } = {180^ \circ }.\)
Vậy tứ giác MNPQ có các góc đối bù nhau.





![[PGD Kinh Môn] thi học kì 2 lớp 8 môn Hóa năm 2020: Cho 6,5 gam kẽm tác dụng hết với V lít dung dịch axit clohidric 1M. Tính thể tích khí thoát ra ở đktc](https://dethikiemtra.com/wp-content/uploads/2020/07/hoa-100x75.png)
