Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Lấy điểm B thuộc đường tròn (O). Qua B kẻ tiếp tuyến với (O) cắt (O’) ở hai điểm C và D. Gọi M là điểm chính giữa của cung CD. Chứng minh ∆ABM vuông tại A.
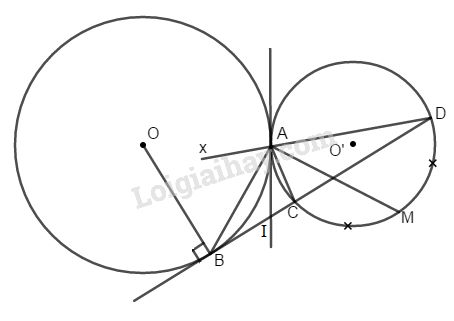
Kẻ tiếp tuyến qua A cắt BD tại I, ta có : \(\widehat {IAC} = \widehat {ADC}\) (1)
(góc giữa tiếp tuyến và một dây bằng góc nội tiếp cùng chắn cung AC)
Advertisements (Quảng cáo)
Lạicó : \(\widehat {IAB} = \widehat {IBA}\) (2)
(tính chất hai tiếp tuyến cắt nhau)
Từ (1) và (2) : \(\widehat {IAC} + \widehat {IAB} = \widehat {ADC} + \widehat {IBA} = \widehat {BAx}\) ( \(\widehat {BAx}\) là góc ngoài của \(∆BAD\)) hay \(\widehat {BAC} = \widehat {{\rm{BAx}}}\), chứng tỏ AB là phân giác của \(\widehat {{\rm{IAx}}}\).
Advertisements (Quảng cáo)
Mặt khác M là điểm chính giữa cung CD nên\(\widehat {CAM} = \widehat {DAM}\) hay AM là phân giác ngoài.
Vậy AB vuông góc AM hay \(∆ABM\) vuông tại A.
