Chia sẻ đề kiểm tra Toán lớp 9 15 phút Chương 2 Đại số: Viết phương trình đường thẳng qua hai điểm A(0; 1) và B(-1; 0)

Bài 1. Viết phương trình đường thẳng qua hai điểm \(A(0; 1)\) và \(B(-1; 0)\).

Bài 2. Cho đường thẳng \(d:y = 3x + m.\) Tìm m để đường thẳng d cắt trục tung tại điểm có tung độ bằng  \(-3\)

Bài 3. Chứng tỏ họ đường thẳng d : \(y = mx + 2m + 1\) luôn đi qua điểm \(A(-2; 1)\).

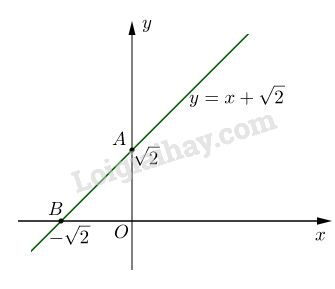
Bài 4. Vẽ đồ thị của hàm số \(y = x + \sqrt 2 \)

Bài 1. Phương trình đường thẳng d có dạng : y = ax + b (a ≠ 0)

Vì \(A \in d \Rightarrow 1 = a.0 + b \Rightarrow b = 1 \)\(\;\Rightarrow y = ax + 1\)

Lại có \(B \in d \Rightarrow 0 = a.\left( { – 1} \right) + 1 \Rightarrow a = 1\)

Vậy phương trình đường thẳng d là \(y = x + 1\).

Bài 2. Theo giả thiết, ta có \(m = -3\)

Bài 3. \(A \in d \Rightarrow 1 = m.\left( { – 2} \right) + 2m + 1\) hay \(1 =  – 2m + 2m + 1\) (luôn đúng)

Chứng tỏ họ đường thẳng d luôn đi qua A.

Bài 4. Bảng giá trị:

Đồ thị là đường thẳng qua hai điểm \(M\left( {0;\sqrt 2 } \right)\) và \(N\left( { – \sqrt 2 ;0} \right)\)

(Dựng hình vuông OPAQ; ở đó \(A(1; 1)\) ⇒ \(OA = \sqrt 2 .\) Sau đó dựng đường tròn tâm O, bán kính OA

\( \Rightarrow OM = \sqrt 2 \) và \(ON = \sqrt 2  \Rightarrow M\left( {0;\sqrt 2 } \right);N\left( { – \sqrt 2 ;0} \right)\) )