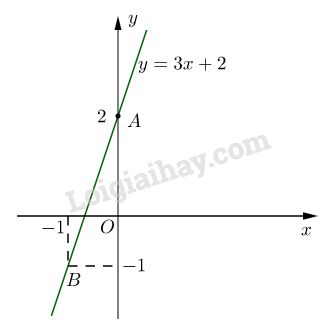
Bài 1. Vẽ đồ thị của hàm số \(y = 3x + 2.\)
Bài 2. Cho hàm số \(y = \left( {m – 2} \right)x + m.\) Tìm m để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 3.
Bài 3. Chứng tỏ rằng họ đường thằng (d) : \(y = \left( {m – 1} \right)x + m\) luôn qua điểm \(A(-1; 1)\) với mọi giá trị m \((m ≠ 1)\)
Bài 4. Cho hàm số \(y = (2m – 1 )x + m\). Tìm m để đồ thị hàm số qua gốc tọa độ.
Advertisements (Quảng cáo)
Bài 1. Bảng giá trị:
|
x |
0 |
-1 |
|
y |
2 |
-1 |
Đồ thị là đường thẳng qua hai điểm \(A(0; 2)\) và \(B(-1; -1)\).
Advertisements (Quảng cáo)
Bài 2. Theo giả thiết, ta có \(m = 3\)
Bài 3. \(A \in \left( d \right) \Rightarrow 1 = \left( {m – 1} \right).\left( { – 1} \right) + m\) hay \(1 = – m + 1 + m,\) luôn đúng với mọi \(m \;(m ≠ 1)\)
Bài 4. Theo giả thiết, ta có: \(0 = (2m – 1).0 + m ⇒ m = 0\).
