2 Đề kiểm tra chất lượng đầu năm Toán lớp 9 năm 2015 – Ma trận đề thi

2 đề Kiểm tra chất lượng đầu năm lớp 9 môn toán (KSCL đầu năm) có đáp án và có dạng ma trận đề thi mới nhất.

Đề số 1:

KIỂM TRA CHẤT LƯỢNG ĐẦU NĂM

Năm học: 2015-2016

Môn thi: TOÁN – Lớp 9

Thời gian: 90 phút (không kể thời gian phát đề)

Ma trận đề thi môn toán lớp 9

Cấp độ   Chủ đề	Nhận biết	Thông hiểu	Vận dụng		Cộng
			Cấp độ thấp	Cấp độ cao
1. Pt bậc nhất một ẩn. ( 16 tiết )	Biết giải phương trình bậc nhất một ẩn. Biết tìm điều kiện xác định của pt chứa ẩn ở mẫu	Biết giải phương trình chứa ẩn ở mẫu	Giải phương trình tích	Vận dụng để giải bài toán bằng cách lập phương trình
Số câu Số điểm. Tỉ lệ %	1 1đ	1 1đ	1 0,5đ	1 1đ	4 3,5đ = 35%
2.Bpt bậc nhất một ẩn. ( 30tiết)	Biết giải bất phương trình và biểu diễn tập nghiệm trên trục số	Biết vận dụng 1 bất đẳng thức cho trước để suy ra 1 bất đẳng thức khác
Số câu Số điểm. Tỉ lệ %	1 1đ	2 1,5đ			3 2,5đ = 25%
3.Tam giác đồng dạng. ( 12 tiết )	Nhận biết các tam giác đồng dạng	Biết áp dụng t/c đường phân giác để tìm tỉ số độ dài đoạn thẳng	Vận dụng để c/m 2 tam giác đồng dạng, c/m đẳng thức hình học
Số câu Số điểm. Tỉ lệ %	1 0,5đ	1 1đ	2 1,5đ		4 3,0đ = 30%
4. Hình lăng trụ đứng. ( 4 tiết )	Biết viết công thức tính diện tích xung quanh hình lăng trụ đúng	Biết áp dụng công thức để tính diện tích xung quanh hình lăng trụ đứng
Số câu Số điểm. Tỉ lệ %	1 0,5đ	1 0,5đ			2 1,0đ = 10%
Tổng số câu Tổng số điểm. Tỉ lệ %	4 3đ	5 4đ	3 2đ	1 1đ	13 10đ

I: ( 2,5đ) Giải các phương trình sau

1.    2x – 4 = 0

2.   3x² – 6x = 0

II: ( 2,5đ )

1. Giải và biểu diễn tập nghiệm của bất phương trình sau trên trục số :

X – 5 > 0

2. Cho a < b so sánh

a. 3a và 3b                             b. – 2a +1 và – 2b + 1

III: ( 1,0đ ) Giải bài toán sau bằng cách lập phương trình

Lúc 5 giờ sáng, một canô xuôi dòng từ bến A đến bến B, rồi ngay lập tức từ bến B trở về A lúc 12 giờ cùng ngày. Tính khoảng cách từ bến A đến B, biết canô đến bến B lúc 8 giờ và vận tốc dòng nước là 3km/h.

IV: ( 3,0đ )

Cho hình vẽ, tìm các cặp tam giác đồng dạng?

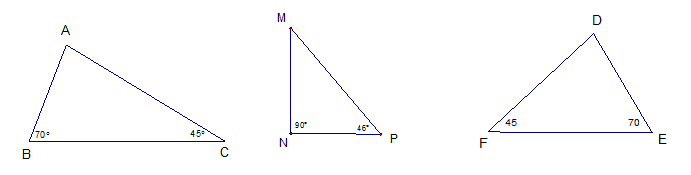
2.   Cho tam giác ABC vuông tại A, có AB = 9cm, AC = 12cm, BC = 15cm, đường cao AH (HBC).

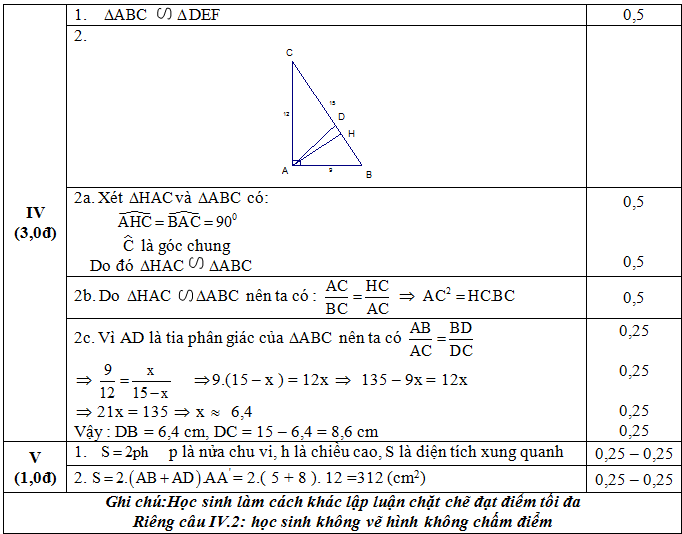
1. Chứng minh ΔHAC đồng dạng  ΔABC
2. Chứng minh rằng AC²=HCBC
3. Cho AD là đường phân giác của tam giác ABC (D ∈BC). Tính độ dài BD và D
   C.( Làm tròn đến chữ số thập phân thứ nhất )

V: ( 1,0đ )

1. Viết công thức tính diện tích xung quanh hình lăng trụ đứng. Giải thích kí hiệu.

2. Tính diện tích xung quanh hình hộp chữ nhật ABCD.A^’B^’C^’D^’, biết AB = 5cm, AD = 8cm, AA^’ = 12cm.

---

Đáp án đề khảo sát chất lượng môn Toán 8 đề số 1

cau 1,2,3

cau 4,5

---

Đề số 2:

MA TRẬN ĐỀ KIỂM TRA:

Cấp độ  Chủ đề	Nhận biết	Thông hiểu	Vận dụng		Cộng
			Cấp độ thấp	Cấp độ cao
1. Phương trình chứa ẩn ở mẫu.	Biết tìm điều kiện xác định của của phương trình	Giải được phương trình chứa ẩn ở mẫu
Số câu Số điểm      Tỉ lệ %	1 (1a) 1 10%	1 (1b) 1 10%			2 2 20%
2. Giải bài toán bằng cách lập phương trình.				Biểu diễn thành thạo mối liên hệ giữa các đại lượng s, t, v để lập phương trình
Số câu Số điểm      Tỉ lệ %				1 (C3) 1 10%	1 1 10%
3. Bất phương trình bậc nhất một ẩn.	Biết giải bất phương trình bậc nhất một ẩn và biểu diễn tập nghiệm trên trục số.	Biết áp dụng các tính chất liên hệ giữa thứ tự với phép cộng, phép nhân để chứng minh bất đẳng thức
Số câu Số điểm     Tỉ lệ %	1(2a) 1 10%	1(2b) 1 10%			2 2 20%
4. Tam giác đổng dạng.		– Biết sử dụng ĐL Py-Ta-Go để tính độ dài cạnh của tam giác vuông. – Biết áp dụng các trường hợp đồng dạng của tam giác vuông để chứng minh hai tam giác vuông đồng dạng	Biết áp dụng các kiến thức đã học để tính tỉ số diện tích của hai tam giác đồng dạng, tính độ dài đoạn thẳng.
Số câu Số điểm Tỉ lệ		2 (4a,4b) 2 20%	2 (4c,4d) 2 20%		4 4 40%
5. Hình hộp chữ nhật	Tái hiện được công thức tính thể tích hình hộp chữ nhật; Tính được thể tích hình hộp chữ nhật.
Số câu Số điểm Tỉ lệ	2(5a,5b) 1 10%				2(5a,5b) 1 10%
Tổng số câu Tổng số điểm Tỉ lệ	4 3 30%	4 4 40%	2 2 20%	1 1 10%	11 10 100%

1: (2đ) Cho phương trình:

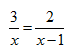
a/ Tìm điều kiện xác định của phương trình.

b/ Giải phương trình trên.

2:  (2đ)

a/ Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số:

x + 2  ≥ 0

b/ Cho a>b, chứng minh:  4a + 3 >  4b + 3.

3: (1đ) Một người đi xe đạp từ A đến B với vận tốc trung bình 12km/h. Lúc về, người đó chỉ đi với vận tốc trung bình 10km/h, nên thời gian về nhiều hơn thời gian đi là 45 phút. Tính độ dài quãng đường AB?

4: (4đ) Cho tam giác ABC vuông tại A, có AB = 6cm, AC = 8cm, đường cao AH ( H ∈ BC).

a/ Tính độ dài BC.

b/ Hãy chỉ ra  các cặp tam giác đồng dạng (viết theo thứ tự các đỉnh tương ứng và giải thích vì sao chúng đồng dạng).

c/ Tính tỉ số diện tích của hai tam giác HBA và HAC.

d/ Cho AD là đường phân giác của góc BAC (D ∈  BC). Tính độ dài DB và DC

5: (1đ)

a/ Viết công thức tính thể tích hình hộp chữ nhật.

b/ Tính thể tích hình hộp chữ nhật ABCDA/B/C/D/ biết AB = 6cm, AA/ = 5cm, AD = 4cm.

---

Đáp án đề KSCL đầu năm môn toán lớp 9 đề số 2

1 (2đ): a/ ĐKXĐ:  x≠0 và x≠1 (1đ)

b/

(1)⇒3(x-1) = 2x

⇔ 3x – 3 = 2x

⇔3x – 2x = 3

⇔x = 3 (TMĐKXĐ)

Vậy phương trình có tập nghiệm là S = {3} (1đ)

2 (2đ):  a/  x + 2≥  0

⇔     x  ≥ -2

Vậy tập nghiệm của bất phương trình là {x/x ≥ -2}  (0,5đ)

+Biểu diễn tập nghiệm trên trục số:

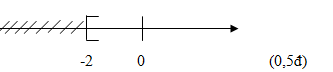 b/ Nhân hai vế của bất phương trình  a>b với 4 ta được:

4a>4b                  (0,5đ)

Cộng 3 vào cả hai vế của bất phương trình này ta được:

4a + 3 > 4b + 3    (0,5đ)

3 (1đ): Gọi độ dài quãng đường AB là x(km), điều kiện x>0    (0,25đ)

Thời gian đi từ A đến B là: x/12(h)

Thời gian về từ B đến A là: x/10 (h)             (0,25đ)

Vì thời gian về nhiều hơn thời gian đi là 45 phút (45 phút = 3/4(h)) nên ta có phương trình: x/10 –  x/12 = 3/4    (0,25đ)

⇔  6x – 5x = 45

⇔  x = 45 (TMĐK)

Vậy độ dài quãng đương AB là 45km.        (0,25đ)

4 (4đ) Giám khảo tự vẽ hình.

a/ Tính BC:  Áp dụng định lý Py-Ta-Go vào tam giác vuông ABC ta có:

BC² = AB² + AC²

BC²  = 6² + 8² =  100

⇒ BC = 10(cm)    (1d).

b/  _vABC đồng dạng _vHBA (vì có góc B chung)

_vABC đồng dạng _vHAC (vì có góc C chung)

_vHBA đồng dạng _vHAC (vì có góc HAB = góc C do cùng phụ với góc B)  (1đ).

c/(1đ) Vì _vHBA đồng dạng _vHAC

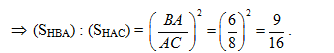
d/ (1đ) Vì AD là đường phân giác của góc BA
C.Áp dụng tính chất đường phân giác của tam giác, ta có:

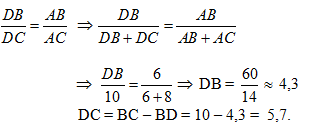
5 (1đ): a/ V = a.b.c, với a,b,c là các kích thước của hình hộp chữ nhật.   (0,5đ)

b/ V =  AB.AD AA^/ =  6.4.5 = 120 cm³.         (0,5đ)