Đề kiểm tra học kì 1 môn Toán lớp 9 của phòng GD quận Hai Bà Trưng, Hà Nội năm học 2018 – 2019: Tìm m để đường thẳng (d) cắt hai trục tọa độ Ox, Oy tạo thành một tam giác có diện tích bằng 9.
UBND QUẬN HAI BÀ TRƯNG ĐỀ KIỂM TRA HỌC KỲ I – MÔN TOÁN LỚP 9
PHÒNG GD VÀ ĐT NĂM HỌC 2018 – 2019
Ngày kiểm tra: 12/12/2018
Thời gian làm bài 90 phút (Không kể thời gian phát đề)
Bài 1. (2đ)
1. Thực hiện phép tính:
a) 2√75 – 8√27 + 4√48 b) √15 – √5)/( √3 – 1) + √(2 – √5)2 – 2√5
2. Giải phương trình: x – 2√(x – 3) = 3
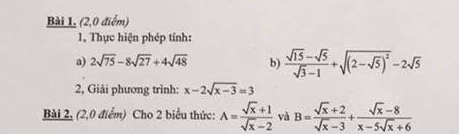
Advertisements (Quảng cáo)
Với x ≥ 0; x ≠ 4; x ≠ 9
a) Tính giá trị của biểu thức A khi x = ¼
b) Rút gọn biểu thức B
c) Tìm tất cả các giá trị nguyên của x để B < A
Bài 3. (2đ)
Advertisements (Quảng cáo)
Cho hàm số y = (m + 1)x + 3 (với m ≠ -1) có đồ thị là đường thẳng (d)
a) Vẽ đồ thị hàm số khi m = 2
b) Tìm m để đường thẳng (d) song song với đường thẳng y = -2x + 1
c) Tìm m để đường thẳng (d) cắt hai trục tọa độ Ox, Oy tạo thành một tam giác có diện tích bằng 9.
Bài 4. (3,5đ) Cho đường tròn (O; R) đường kính AB. Điểm C thuộc đường tròn sao cho AC > CB; C khác A và B. Kẻ CH vuông góc với AB tại H; kẻ OI vuông góc với AC tại I.
a) Chứng minh 4 điểm C, H, O, I cùng thuộc một đường tròn.
b) Kẻ tiếp tuyến Ax của đường tròn (O; R), tia OI cắt Ax tại M, chứng minh OLOM = R2. Tính độ dài đoạn OI biết OM = 2R và R = 6cm.
c) Gọi giao điểm BM với CH là K. Chứng minh tam giác AMO đồng dạng với tam giác HCB và KC = KH.
d) Giả sử (O; R) cố định, điểm C thay đổi trên đường tròn nhưng vẫn thỏa mãn điều kiện của đề bài. Xác định vị trí của C để chu vi của tam giác OHC đạt giá trị lớn nhất? Tìm giá trị lớn nhất đó theo R.
Bài 5: (0,5đ) Cho các số thực x, y, z > 0 và x + 2y + 3z ≥ 20.
Tìm giá trị nhỏ nhất của biểu thức P = x + y + z + 3/x + 9/2y + 4/z
