Đề kiểm tra 15 phút môn Toán lớp 9 Chương 3: Chứng minh rằng tứ giác OBDK nội tiếp

M là một điểm thuộc cung nhỏ BC. Tiếp tuyến tại M cắt AB, AC lần lượt ở D và E. Gọi I và K lần lượt là giao điểm của OD, OE với BC. Chứng minh rằng tứ giác OBDK nội tiếp.

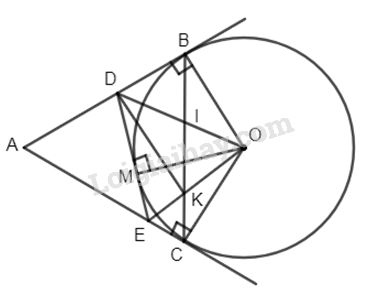
Dễ thấy tứ giác ABOC nội tiếp ( vì \(\widehat {ABO} = \widehat {ACO} = 90^\circ \) tính chất tiếp tuyến) \( \Rightarrow \widehat {BAC} + \widehat {BOC} = 180^\circ \). Do đó \(\widehat {BOC} = 180^\circ  – \widehat A\).

Theo (tính chất hai tiếp tuyến cắt nhau, ta có OD, OE lần lượt là phân giác của hai góc kề \(\widehat {BOM}\) và \(\widehat {MOC}\) nên \(\widehat {DOE} =\dfrac {{180^\circ  – \widehat A}}{ 2}\)         (1)

Mặt khác : ∆ABC cân ( AB = AC) nên \(\widehat {ABC} = \widehat {ACB} = \dfrac{{180^\circ  – \widehat A} }{ 2}\)    (2)

Từ (1) và (2) \( \Rightarrow \widehat {DOE} = \widehat {ABC}\) hay

Do đó bốn điểm O, B, K, D cùng nằm trên một đường tròn, hay tứ giác OBDK nội tiếp.