Đề kiểm tra 45 phút Chương 2 Hàm số bậc nhất Đại số 9: Tìm điều kiện xác định của hàm số

Bài 1. Tìm điều kiện xác định của hàm số:

a. \(y = {1 \over {x – 1}}\)

b. \(y = \sqrt {1 – x} \)

Bài 2. Chứng minh rằng hàm số \(y = f\left( x \right) =  – x + 1\) nghịch biến trên \(\mathbb R\).

So sánh \(f\left( {1 – \sqrt 2 } \right)\) và \(f\left( {1 + \sqrt 2 } \right)\)

Bài 3. Cho hàm số \(y = \sqrt 2 x + 1\)

a. Vẽ đồ thị (d) của hàm số

b. Tính góc tạo bởi (d) và trục Ox (làm tròn đến phút)

c. Viết phương trình đường thẳng (d’) qua O và song song với đường thẳng \(y = \sqrt 2 x + 1\)

Bài 1. a. \({1 \over {x – 1}}\) xác định \(⇔ x – 1 ≠ 0 ⇔ x ≠ 1\).

b. \(\sqrt {1 – x} \) xác định \(⇔ 1 – x ≥ 0 ⇔ x ≤ 1\).

Bài 2. Với \({x_1},{\rm{ }}{x_2}\)bất kì thuộc \(\mathbb R\) và \({x_1} < {\rm{ }}{x_2}\). Ta có:

\(\eqalign{  & f\left( {{x_1}} \right) =  – {x_1} + 1;f\left( {{x_2}} \right) =  – {x_2} + 1\cr& \Rightarrow f\left( {{x_1}} \right) – f\left( {{x_2}} \right) =  – \left( {{x_1} – {x_2}} \right)  \cr  & \text{Vì }{x_1} < {x_2} \Rightarrow {x_1} – {x_2} < 0 \cr&\Rightarrow  – \left( {{x_1} – {x_2}} \right) > 0  \cr  &  \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right) \cr} \)

Vậy hàm số đã cho nghịch biến trên \(\mathbb R\).

Ta có: \(1 – \sqrt 2  < 1 + \sqrt 2 \) và hàm số \(y = f\left( x \right) =  – x + 1\) nghịch biến \( \Rightarrow f\left( {1 – \sqrt 2 } \right) > f\left( {1 + \sqrt 2 } \right)\)

Bài 3. a. Bảng giá trị:

Đồ thị của hàm số là đường thẳng (d) đi qua hai điểm \(A\left( { – \sqrt 2 ; – 1} \right)\) và \(B(0; 1)\).

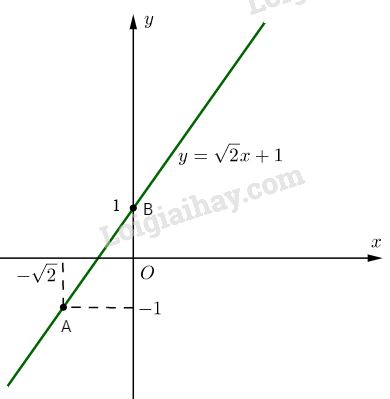
b. Trong tam giác ABC với \(C(0 ; -1)\), ta có:

\(\tan \widehat {BAC} = {2 \over {\sqrt 2 }} = \sqrt 2\)

\(  \Rightarrow \widehat {BAC} = 54^\circ 44’\)

Ta có: \(\widehat {BDO} = \widehat {BAC} = \alpha  \Rightarrow \alpha  \approx 54^\circ 44’\)

c. Phương trình (d’) có dạng: \(y = \sqrt 2 x + b\,\left( {b \ne 1} \right)\)

\(O ∈ (d’) ⇒ b = 0\). Vậy \(y = \sqrt 2 x\)